人教版五年级数学上册 第三单元第5课时《循环小数》精品教学方案
文档属性
| 名称 | 人教版五年级数学上册 第三单元第5课时《循环小数》精品教学方案 |

|
|
| 格式 | docx | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:20:38 | ||
图片预览


文档简介
第三单元 小数除法
第5课时 循环小数
教学内容分析:
本课是人教版数学五年级上册“小数除法”的内容,是“数与代数”教学领域的重要组成部分。循环小数是在学生学习了小数除法的意义、小数除法的计算及商的近似数的基础上进行教学的。这部分内容概念较多,又比较抽象,是教学的一个难点。例7通过学生对算式的观察发现两数相除得到循环小数时的现象,例8根据两个算式商的特点引出循环小数和循环节的概念,并学习简便写法。在练习中又引出了无限小数和有限小数的概念。以前学生对小数概念的认识仅限于有限小数,学习了循环小数以后,小数概念的内涵进一步扩展了,学生认识到除了有限小数以外,还有无限小数,循环小数就是一种无限小数。 从知识角度来看,“循环小数”是数概念的一次重要扩展,即从“有限”扩展到“无限”,是学生对数的认识的一个飞跃。
教学目标:
认识循环小数,理解循环小数产生的原因,并能正确使用循环小数表示商。
认识循环节,能正确进行循环小数的简写。
3. 在猜想、验证过程中进一步提高观察、比较、抽象、概括能力,感受数学的简洁美。
教学重点:
认识循环小数,正确使用循环小数表示商。
教学难点:
理解循环小数产生的原因。
教学过程:
教学环节 教师活动 学生活动 设计意图
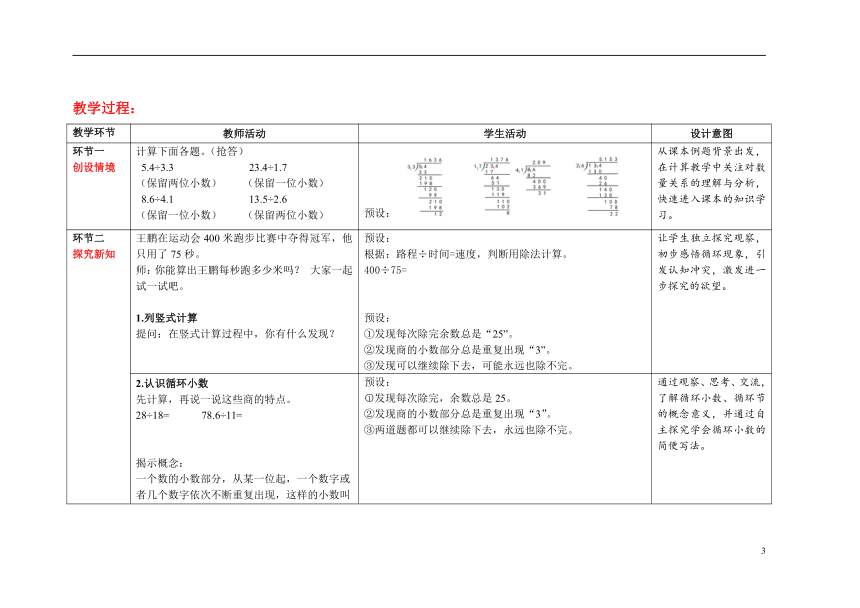
环节一 创设情境 计算下面各题。(抢答) 5.4÷3.3 23.4÷1.7 (保留两位小数) (保留一位小数) 8.6÷4.1 13.5÷2.6 (保留一位小数) (保留两位小数) 预设: 从课本例题背景出发,在计算教学中关注对数量关系的理解与分析,快速进入课本的知识学习。
环节二 探究新知 王鹏在运动会400米跑步比赛中夺得冠军,他只用了75秒。 师:你能算出王鹏每秒跑多少米吗? 大家一起试一试吧。 1.列竖式计算 提问:在竖式计算过程中,你有什么发现? 预设: 根据:路程÷时间=速度,判断用除法计算。 400÷75= 预设: ①发现每次除完余数总是“25”。 ②发现商的小数部分总是重复出现“3”。 ③发现可以继续除下去,可能永远也除不完。 让学生独立探究观察,初步感悟循环现象,引发认知冲突,激发进一步探究的欲望。
2.认识循环小数 先计算,再说一说这些商的特点。 28÷18= 78.6÷11= 揭示概念: 一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。像上面的1.555…和7.14545…都是循环小数。 一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。 预设: 发现每次除完,余数总是25。 ②发现商的小数部分总是重复出现“3”。 ③两道题都可以继续除下去,永远也除不完。 预设:只写第一个循环节,并在这个循环节的首位和末位的数字上面各记一个圆点。 预设1:通过计算,商的小数部分3一直不断出现,所以商是循环小数,循环节是3。 预设2:当余数重复出现两次的时候,商是循环小数。 通过观察、思考、交流,了解循环小数、循环节的概念意义,并通过自主探究学会循环小数的简便写法。
3.探究循环小数的简便写法 课件呈现3个简便写法的例子。 5.333…的循环节是3 写作 5.3 1.555…的循环节是5 写作1.5 6.9258258…的循环节是258 写作 6.9258 提出问题:你发现循环小数简写的方法了吗? 师:计算1.3÷3,它的商是循环小数吗?怎样快速判断呢? 小结:当余数重复出现两次的时候,商就是循环小数。
通过练习,引导学生在计算中,感悟循环现象,体会循环小数产生的原因是由于余数的重复出现导致商重复出现。
环节三 巩固练习 用简便形式写成下面的循环小数。 4.333… 1.746746… 0.105353… 2 计算下面各题。(除不尽的先用循环小数表示所得的商。) 15÷16= 1.5÷7= 提出问题:第二个算式的商是不是循环小数? 思考:两个数相除,如果不能得到整数商,所得的商会有哪些情况?(独立思考,然后小组讨论) 教师小结:小数部分的位数有限的小数是有限小数。例如,0.9375是一个有限小数,小数部分的位数无限的小数是无限小数。例如,0.2就是一个无限小数。 3:把下面的数按照从小到大的顺序排列。 9.0 9.8 9.8 9.88 ( )<( )<( )<( ) 判断上面四个数哪些是无限小数? 预设: 预设:15÷16=0.9375 1.5÷7=0.2142857142857… 预设1:第二个算式的商是循环小数,因为余数部分没有依次重复出现。 预设2:主要看余数部分有无依次不断重复出现。 预设1:商是循环小数。 预设2:商是小数。 预设1: 预设2: 9.808是有限小数,其他3个都是无限小数。 采用练习形式,引导学生深入思考循环小数产生的原因是由于余数的重复出现,而并不只是看商中有一个数字重复出现就可以的。 巩固基础知识与基本技能。通过学生对习题的完成情况,反思教学目标达成情况。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 预设1:知道什么是循环小数。一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。 预设2:知道怎样快速判断两个数相除是否得到一个循环小数。余数重复出现两次。 鼓励学生畅谈自己的收获和体会,在师生合作中,从数的分类角度梳理结构图。
环节五 布置作业 教材P36第6题、第9题
1
第5课时 循环小数
教学内容分析:
本课是人教版数学五年级上册“小数除法”的内容,是“数与代数”教学领域的重要组成部分。循环小数是在学生学习了小数除法的意义、小数除法的计算及商的近似数的基础上进行教学的。这部分内容概念较多,又比较抽象,是教学的一个难点。例7通过学生对算式的观察发现两数相除得到循环小数时的现象,例8根据两个算式商的特点引出循环小数和循环节的概念,并学习简便写法。在练习中又引出了无限小数和有限小数的概念。以前学生对小数概念的认识仅限于有限小数,学习了循环小数以后,小数概念的内涵进一步扩展了,学生认识到除了有限小数以外,还有无限小数,循环小数就是一种无限小数。 从知识角度来看,“循环小数”是数概念的一次重要扩展,即从“有限”扩展到“无限”,是学生对数的认识的一个飞跃。
教学目标:
认识循环小数,理解循环小数产生的原因,并能正确使用循环小数表示商。
认识循环节,能正确进行循环小数的简写。
3. 在猜想、验证过程中进一步提高观察、比较、抽象、概括能力,感受数学的简洁美。
教学重点:
认识循环小数,正确使用循环小数表示商。
教学难点:
理解循环小数产生的原因。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 计算下面各题。(抢答) 5.4÷3.3 23.4÷1.7 (保留两位小数) (保留一位小数) 8.6÷4.1 13.5÷2.6 (保留一位小数) (保留两位小数) 预设: 从课本例题背景出发,在计算教学中关注对数量关系的理解与分析,快速进入课本的知识学习。
环节二 探究新知 王鹏在运动会400米跑步比赛中夺得冠军,他只用了75秒。 师:你能算出王鹏每秒跑多少米吗? 大家一起试一试吧。 1.列竖式计算 提问:在竖式计算过程中,你有什么发现? 预设: 根据:路程÷时间=速度,判断用除法计算。 400÷75= 预设: ①发现每次除完余数总是“25”。 ②发现商的小数部分总是重复出现“3”。 ③发现可以继续除下去,可能永远也除不完。 让学生独立探究观察,初步感悟循环现象,引发认知冲突,激发进一步探究的欲望。
2.认识循环小数 先计算,再说一说这些商的特点。 28÷18= 78.6÷11= 揭示概念: 一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。像上面的1.555…和7.14545…都是循环小数。 一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。 预设: 发现每次除完,余数总是25。 ②发现商的小数部分总是重复出现“3”。 ③两道题都可以继续除下去,永远也除不完。 预设:只写第一个循环节,并在这个循环节的首位和末位的数字上面各记一个圆点。 预设1:通过计算,商的小数部分3一直不断出现,所以商是循环小数,循环节是3。 预设2:当余数重复出现两次的时候,商是循环小数。 通过观察、思考、交流,了解循环小数、循环节的概念意义,并通过自主探究学会循环小数的简便写法。
3.探究循环小数的简便写法 课件呈现3个简便写法的例子。 5.333…的循环节是3 写作 5.3 1.555…的循环节是5 写作1.5 6.9258258…的循环节是258 写作 6.9258 提出问题:你发现循环小数简写的方法了吗? 师:计算1.3÷3,它的商是循环小数吗?怎样快速判断呢? 小结:当余数重复出现两次的时候,商就是循环小数。
通过练习,引导学生在计算中,感悟循环现象,体会循环小数产生的原因是由于余数的重复出现导致商重复出现。
环节三 巩固练习 用简便形式写成下面的循环小数。 4.333… 1.746746… 0.105353… 2 计算下面各题。(除不尽的先用循环小数表示所得的商。) 15÷16= 1.5÷7= 提出问题:第二个算式的商是不是循环小数? 思考:两个数相除,如果不能得到整数商,所得的商会有哪些情况?(独立思考,然后小组讨论) 教师小结:小数部分的位数有限的小数是有限小数。例如,0.9375是一个有限小数,小数部分的位数无限的小数是无限小数。例如,0.2就是一个无限小数。 3:把下面的数按照从小到大的顺序排列。 9.0 9.8 9.8 9.88 ( )<( )<( )<( ) 判断上面四个数哪些是无限小数? 预设: 预设:15÷16=0.9375 1.5÷7=0.2142857142857… 预设1:第二个算式的商是循环小数,因为余数部分没有依次重复出现。 预设2:主要看余数部分有无依次不断重复出现。 预设1:商是循环小数。 预设2:商是小数。 预设1: 预设2: 9.808是有限小数,其他3个都是无限小数。 采用练习形式,引导学生深入思考循环小数产生的原因是由于余数的重复出现,而并不只是看商中有一个数字重复出现就可以的。 巩固基础知识与基本技能。通过学生对习题的完成情况,反思教学目标达成情况。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 预设1:知道什么是循环小数。一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。 预设2:知道怎样快速判断两个数相除是否得到一个循环小数。余数重复出现两次。 鼓励学生畅谈自己的收获和体会,在师生合作中,从数的分类角度梳理结构图。
环节五 布置作业 教材P36第6题、第9题
1
