人教版五年级数学上册 第四单元第2课时《摸球实验》精品教学方案(表格式)
文档属性
| 名称 | 人教版五年级数学上册 第四单元第2课时《摸球实验》精品教学方案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 136.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:21:46 | ||
图片预览


文档简介
第四单元 可能性
第2课时 摸球实验
教学内容分析:
本课是人教版数学五年级上册“可能性”内容的第二课时,在上一课中学生已经体验了事件发生的确定性和不确定性,知道了可能性是有大小的,也知道可能性的大小与数量的多少有关。这节课继续沿用上一节的“摸物体游戏”情景,不同的是上一课是已知盒内不同颜色棋子的个数猜测摸出的结果,而本课是根据摸球实验得到的结果反推盒内球的情况,即根据实验结果进行推测和判断,从而进一步体会随机事件发生的统计规律性。同时通过动手试验——猜测说理——验证,培养学生的动手操作、同伴合作、说理表达、推理等能力。
教学目标:
1. 能根据随机现象结果发生的可能性的大小进行推测,进一步体会随机事件发生的统计规律性。
2. 让学生经历亲身体验的过程,在观察、思考、讨论、交流中探索新知。
3. 培养学生的动手操作、同伴合作、说理表达、推理等能力。
教学重点:
能根据随机现象结果发生的可能性的大小进行推测。
教学难点:
体会随机事件发生的统计规律性。
教学过程:
教学 环节 教师活动 学生活动 设计意图
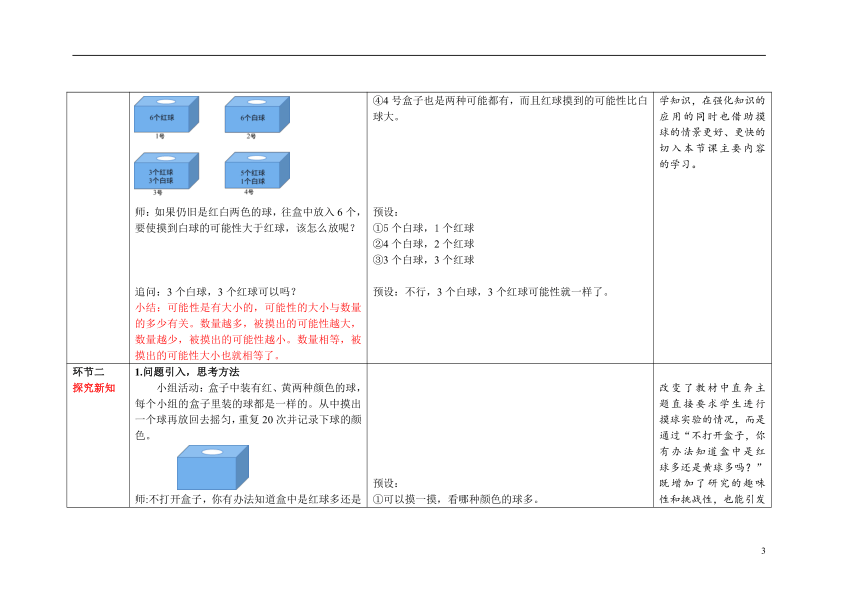
环节一 创设情境 同学们,上一节课我们一起研究了可能性,请你分别从下面的盒子中任意摸出1个球,想一想,可能摸到什么颜色的球? 师:如果仍旧是红白两色的球,往盒中放入6个,要使摸到白球的可能性大于红球,该怎么放呢? 追问:3个白球,3个红球可以吗? 小结:可能性是有大小的,可能性的大小与数量的多少有关。数量越多,被摸出的可能性越大,数量越少,被摸出的可能性越小。数量相等,被摸出的可能性大小也就相等了。 预设: ①1号盒子全部是红球,一定摸出红球。 ②2号盒子全部是白球,一定摸出白球。 ③3号盒子红球和白球都有可能摸出,而且两种球数量一样,所以摸出的可能性一样大。 ④4号盒子也是两种可能都有,而且红球摸到的可能性比白球大。 预设: ①5个白球,1个红球 ②4个白球,2个红球 ③3个白球,3个红球 预设:不行,3个白球,3个红球可能性就一样了。 复习引入,通过摸球的例子回顾上一节课所学知识,在强化知识的应用的同时也借助摸球的情景更好、更快的切入本节课主要内容的学习。
环节二 探究新知 1.问题引入,思考方法 小组活动:盒子中装有红、黄两种颜色的球,每个小组的盒子里装的球都是一样的。从中摸出一个球再放回去摇匀,重复20次并记录下球的颜色。 师:不打开盒子,你有办法知道盒中是红球多还是黄球多吗? 师:你们真厉害,都想到了摸球实验。 师:你觉得他们说得对吗? 小结:是啊,不能仅凭一、两次的摸球结果就轻易做出判断,多次试验才更能说明问题。 2.实验操作,大胆猜想 摸球实验要求:小组合作进行摸球实验,从中摸出一个球后再放回去摇匀,每组重复20次并记录下球的颜色。 注意:实验的时候不要看盒中球的情况; 小组内成员要分工合作,有序完成。 呈现各组的实验结果: 师:根据实验结果,你觉得盒中哪种颜色的球更多? 小结:试计算一下8个小组的总和,次数越多可能和实际情况越接近! 呈现8个小组的合计结果: 根据合计的结果,你会得到怎样的推测呢? 追问:那一定是红球多吗? 小结:的确不一定,到底哪种颜色的球多要打开盒子才能确定。但摸球实验中红球摸到的次数更多,所以我们可以推断红球摸到的可能性更大。 3.情况对比,得出结论 预设: ①可以摸一摸,看哪种颜色的球多。 ②可以做一个摸球实验,看哪种颜色摸到的可能性大,哪种颜色的球就多。 预设: 同学1:我两次都摸到了红球,盒中一定是红球多。 同学2:我只摸了一次就摸到黄球,一定是黄球多 预设: ①不对,只摸了这么几次也许只是巧合。 ②摸得次数太少,也许下一次摸到的颜色就不一样了。 小组合作,摸球实验 预设:大部分小组都是红球摸到的次数多,所以红球的个数可能比黄球多。 预设:总体上看,黄球摸到的次数少,所以红球的个数可能比黄球多。 预设:①红球的个数只是可能比黄球多,但不能确定。 ②要打开才能确定到底是不是红球多。 改变了教材中直奔主题直接要求学生进行摸球实验的情况,而是通过“不打开盒子,你有办法知道盒中是红球多还是黄球多吗?”既增加了研究的趣味性和挑战性,也能引发孩子更深入地思考。 通过两位孩子摸球情况的呈现,让孩子感受到多次实验的必要性。 从两位孩子的摸球结果到小组的摸球结果再到全班的结果合计,在感受到单次试验结果的不确定性的同时,体会大量实验结果的统计规律。
环节三 巩固新知 1 选择 (1)一个袋子里放着8颗形状、大小、质量完全一样的围棋子。聪聪从中任意摸出一颗,记录它的颜色后放回,摇匀后再摸,重复摸了5次,都是白棋子。根据数据分析,袋子中( )。 A.一定只有白棋子 B.可能没有白棋子 C.可能只有白棋子 D.一定没有白棋子 (2)盒子里装有黑、白两种颜色的球,明明从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色:黑球17次,白球3次。如果明明再摸一次,下面哪句话的描述是正确的?( ) A.一定摸到黑球 B.一定摸到白球 C.摸到白球的可能性比较大 D.摸到黑球的可能性比较大 2 从盒子中摸大小相同的球,要使摸到红球的可能性最小,摸到白球的可能性最大,还有可能摸到黄球。 (1)请你根据要求在下面的方框中画出你的想法。 (2)盒子中至少要放( )个球。 独立完成后反馈。 针对第二个问题提问:至少是什么意思?该怎么思考? 答案:C ①5次都摸到白棋子,说明一定有白棋子,所以B、D不对。 ②但不一定全是白棋子,也有可能有黑棋子,只是没有摸到而已,所以A不对。 答案:D ①黑球、白球都摸到 ②黑球17次,白球3次,说明黑球的个数可能比白球多。 (1)答案不唯一 ①我放了2个红球、4个黄球、7个白球。 ②我放了3个红球、4个黄球、5个白球。 ③可以很多种放法,只要红色个数最少,白色个数最多就可以了。 (2)6 ①至少就是要符合要求,但个数还要最少。 ②先想红球最少,最少是1个;白球最多,但多也要保证少,所以2个。但是黄球也要有,如果黄球1个就和红球一样多,不行。如果黄球2个就和白球一样多,所以只能增加白球的个数,白球变为3个,一共6个。 两道选择题进一步提升根据实验数据分析来进行可能性推测的能力,感受统计的规律性。 本题是上一课时与本课所学知识的融合,强调知识的应用,同时通过球的颜色设计、至少放几个球的思考,提升学生的逻辑推理能力。
环节四 课堂小结 你有什么收获? 知道了可以通过实验可以推测个数多少的可能,但是不能完全确定最终的结果。 摸到的次数多,数量可能就多。 摸到的次数少,数量可能就少。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P47练习十一 第4题、第6题、第7题。
1
第2课时 摸球实验
教学内容分析:
本课是人教版数学五年级上册“可能性”内容的第二课时,在上一课中学生已经体验了事件发生的确定性和不确定性,知道了可能性是有大小的,也知道可能性的大小与数量的多少有关。这节课继续沿用上一节的“摸物体游戏”情景,不同的是上一课是已知盒内不同颜色棋子的个数猜测摸出的结果,而本课是根据摸球实验得到的结果反推盒内球的情况,即根据实验结果进行推测和判断,从而进一步体会随机事件发生的统计规律性。同时通过动手试验——猜测说理——验证,培养学生的动手操作、同伴合作、说理表达、推理等能力。
教学目标:
1. 能根据随机现象结果发生的可能性的大小进行推测,进一步体会随机事件发生的统计规律性。
2. 让学生经历亲身体验的过程,在观察、思考、讨论、交流中探索新知。
3. 培养学生的动手操作、同伴合作、说理表达、推理等能力。
教学重点:
能根据随机现象结果发生的可能性的大小进行推测。
教学难点:
体会随机事件发生的统计规律性。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 同学们,上一节课我们一起研究了可能性,请你分别从下面的盒子中任意摸出1个球,想一想,可能摸到什么颜色的球? 师:如果仍旧是红白两色的球,往盒中放入6个,要使摸到白球的可能性大于红球,该怎么放呢? 追问:3个白球,3个红球可以吗? 小结:可能性是有大小的,可能性的大小与数量的多少有关。数量越多,被摸出的可能性越大,数量越少,被摸出的可能性越小。数量相等,被摸出的可能性大小也就相等了。 预设: ①1号盒子全部是红球,一定摸出红球。 ②2号盒子全部是白球,一定摸出白球。 ③3号盒子红球和白球都有可能摸出,而且两种球数量一样,所以摸出的可能性一样大。 ④4号盒子也是两种可能都有,而且红球摸到的可能性比白球大。 预设: ①5个白球,1个红球 ②4个白球,2个红球 ③3个白球,3个红球 预设:不行,3个白球,3个红球可能性就一样了。 复习引入,通过摸球的例子回顾上一节课所学知识,在强化知识的应用的同时也借助摸球的情景更好、更快的切入本节课主要内容的学习。
环节二 探究新知 1.问题引入,思考方法 小组活动:盒子中装有红、黄两种颜色的球,每个小组的盒子里装的球都是一样的。从中摸出一个球再放回去摇匀,重复20次并记录下球的颜色。 师:不打开盒子,你有办法知道盒中是红球多还是黄球多吗? 师:你们真厉害,都想到了摸球实验。 师:你觉得他们说得对吗? 小结:是啊,不能仅凭一、两次的摸球结果就轻易做出判断,多次试验才更能说明问题。 2.实验操作,大胆猜想 摸球实验要求:小组合作进行摸球实验,从中摸出一个球后再放回去摇匀,每组重复20次并记录下球的颜色。 注意:实验的时候不要看盒中球的情况; 小组内成员要分工合作,有序完成。 呈现各组的实验结果: 师:根据实验结果,你觉得盒中哪种颜色的球更多? 小结:试计算一下8个小组的总和,次数越多可能和实际情况越接近! 呈现8个小组的合计结果: 根据合计的结果,你会得到怎样的推测呢? 追问:那一定是红球多吗? 小结:的确不一定,到底哪种颜色的球多要打开盒子才能确定。但摸球实验中红球摸到的次数更多,所以我们可以推断红球摸到的可能性更大。 3.情况对比,得出结论 预设: ①可以摸一摸,看哪种颜色的球多。 ②可以做一个摸球实验,看哪种颜色摸到的可能性大,哪种颜色的球就多。 预设: 同学1:我两次都摸到了红球,盒中一定是红球多。 同学2:我只摸了一次就摸到黄球,一定是黄球多 预设: ①不对,只摸了这么几次也许只是巧合。 ②摸得次数太少,也许下一次摸到的颜色就不一样了。 小组合作,摸球实验 预设:大部分小组都是红球摸到的次数多,所以红球的个数可能比黄球多。 预设:总体上看,黄球摸到的次数少,所以红球的个数可能比黄球多。 预设:①红球的个数只是可能比黄球多,但不能确定。 ②要打开才能确定到底是不是红球多。 改变了教材中直奔主题直接要求学生进行摸球实验的情况,而是通过“不打开盒子,你有办法知道盒中是红球多还是黄球多吗?”既增加了研究的趣味性和挑战性,也能引发孩子更深入地思考。 通过两位孩子摸球情况的呈现,让孩子感受到多次实验的必要性。 从两位孩子的摸球结果到小组的摸球结果再到全班的结果合计,在感受到单次试验结果的不确定性的同时,体会大量实验结果的统计规律。
环节三 巩固新知 1 选择 (1)一个袋子里放着8颗形状、大小、质量完全一样的围棋子。聪聪从中任意摸出一颗,记录它的颜色后放回,摇匀后再摸,重复摸了5次,都是白棋子。根据数据分析,袋子中( )。 A.一定只有白棋子 B.可能没有白棋子 C.可能只有白棋子 D.一定没有白棋子 (2)盒子里装有黑、白两种颜色的球,明明从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色:黑球17次,白球3次。如果明明再摸一次,下面哪句话的描述是正确的?( ) A.一定摸到黑球 B.一定摸到白球 C.摸到白球的可能性比较大 D.摸到黑球的可能性比较大 2 从盒子中摸大小相同的球,要使摸到红球的可能性最小,摸到白球的可能性最大,还有可能摸到黄球。 (1)请你根据要求在下面的方框中画出你的想法。 (2)盒子中至少要放( )个球。 独立完成后反馈。 针对第二个问题提问:至少是什么意思?该怎么思考? 答案:C ①5次都摸到白棋子,说明一定有白棋子,所以B、D不对。 ②但不一定全是白棋子,也有可能有黑棋子,只是没有摸到而已,所以A不对。 答案:D ①黑球、白球都摸到 ②黑球17次,白球3次,说明黑球的个数可能比白球多。 (1)答案不唯一 ①我放了2个红球、4个黄球、7个白球。 ②我放了3个红球、4个黄球、5个白球。 ③可以很多种放法,只要红色个数最少,白色个数最多就可以了。 (2)6 ①至少就是要符合要求,但个数还要最少。 ②先想红球最少,最少是1个;白球最多,但多也要保证少,所以2个。但是黄球也要有,如果黄球1个就和红球一样多,不行。如果黄球2个就和白球一样多,所以只能增加白球的个数,白球变为3个,一共6个。 两道选择题进一步提升根据实验数据分析来进行可能性推测的能力,感受统计的规律性。 本题是上一课时与本课所学知识的融合,强调知识的应用,同时通过球的颜色设计、至少放几个球的思考,提升学生的逻辑推理能力。
环节四 课堂小结 你有什么收获? 知道了可以通过实验可以推测个数多少的可能,但是不能完全确定最终的结果。 摸到的次数多,数量可能就多。 摸到的次数少,数量可能就少。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P47练习十一 第4题、第6题、第7题。
1
