第九章 专题八 方程(组)与一元一次不等式组的应用(1)一发现限制条件 核心考点训练(含答案)
文档属性
| 名称 | 第九章 专题八 方程(组)与一元一次不等式组的应用(1)一发现限制条件 核心考点训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 77.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 14:37:12 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章一元一次不等式
专题八方程(组)与一元一次不等式组的应用(1)一发现限制条件
01.有若干学生住若干宿舍,如果每间住3人则余8人;如果每间住5人,则最后一间不空也不满,问共有多少学生及多少宿舍
02.某校每年冬季烧煤取暖时间为4个月,如果每月比计划多烧煤,那么取暖用煤总量将超过;如果每月比计划少烧煤,那么取暖用煤总量将不足,该校计划每月烧煤多少吨?
03.某村计划向该村村民提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出15只母羊,若每户发放母羊7只,则有一户可分得母羊,但不足3只.这批种羊共有多少只
04.为庆祝国庆节的到来,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在金山大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来;
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
05.某房地产开发公司计划建两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
(1)该公司对这两种户型住房有哪几种建房方案
(2)该公司所建住房可全部售出,则如何建房获得利润最大
(3)根据市场调查,每套型住房的售价不会改变,每套型住房的售价将会提高万元,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大 (注:利润售价-成本)
成本(万元/套) 25 28
售价(万元/套) 30 34
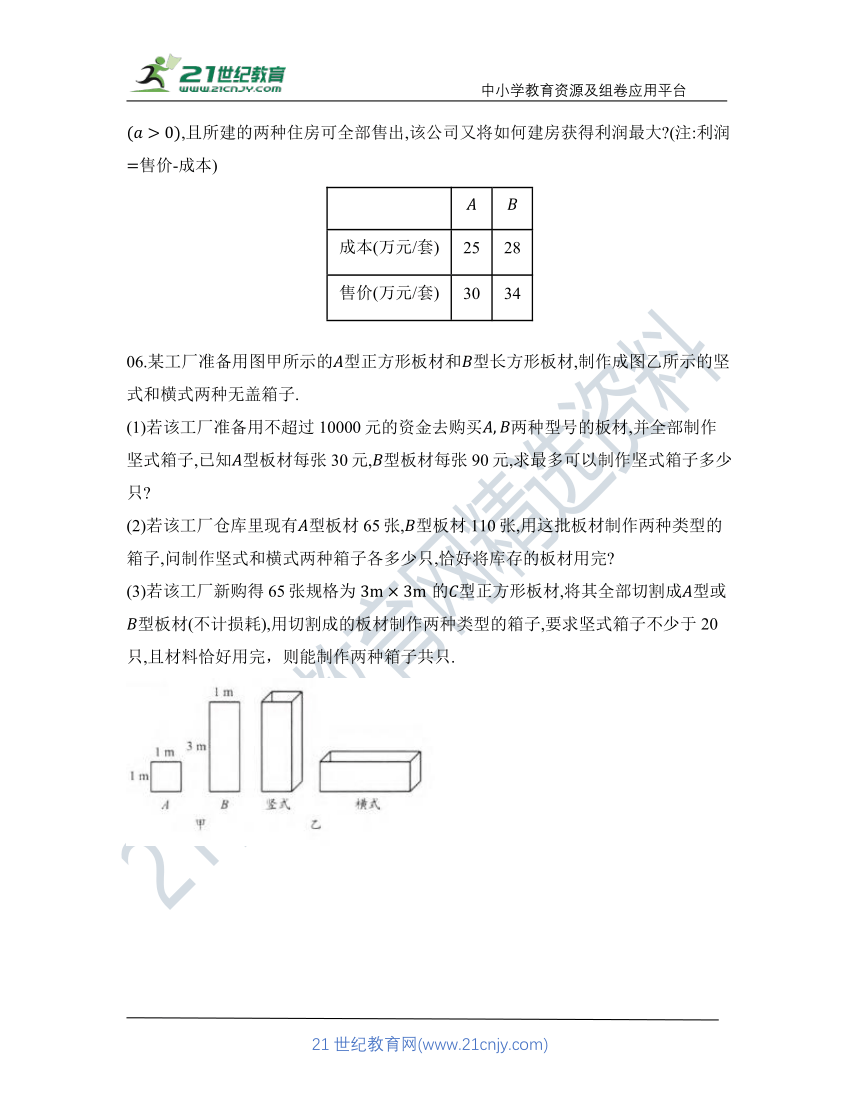
06.某工厂准备用图甲所示的型正方形板材和型长方形板材,制作成图乙所示的坚式和横式两种无盖箱子.
(1)若该工厂准备用不超过10000元的资金去购买两种型号的板材,并全部制作坚式箱子,已知型板材每张30元,型板材每张90元,求最多可以制作坚式箱子多少只
(2)若该工厂仓库里现有型板材65张,型板材110张,用这批板材制作两种类型的箱子,问制作坚式和横式两种箱子各多少只,恰好将库存的板材用完
(3)若该工厂新购得65张规格为的型正方形板材,将其全部切割成型或型板材(不计损耗),用切割成的板材制作两种类型的箱子,要求坚式箱子不少于20只,且材料恰好用完,则能制作两种箱子共只.
专题八方程(组)与一元一次不等式组的应用(1)一发现限制条件
1.解:设有间宿舍,则有个学生,依题意,得,解得,满足此式的整数等于5或6,因而相应地等于23或26.
答:有23名学生及5间宿舍或26名学生及6间宿舍.
2.解:设该校计划每月烧焟,依题意,得,由(1),得;由(2),得,
故不等式组的解集为,答:该校计划每月烧煠多于而少于.
3.解:设该村共有户,则公羊共有只,母羊共有只,由题意知:解得为整数,,这批种羊共有:(只)
答:这批种羊共有75只.
4.解:(1)设搭配种造型个,则种造型为个.
依题意,得:,解这个不等式组,得:.
是整数,可取可设计三种搭配方案:
(1)种园艺造型31个,种园艺造型19个;(2)种园艺造型32个,种园艺造型18个;(3)种园艺造型33个,种园艺造型17个.
(2)由于种造型的造价成本高于种造型成本,种造型越少,成本越低,
故应选择方案(3)成本最低,最低成本为:(元).
5.解:(1)有三种建房方案:型48套,型32套;
型49套,型31套;型50套,型30套.
(2)设该公司建房获得利润为(万元),
由建房成本和售价表可知,型住房获利:(万元/套);
型住房获利:(万元/套),型住房每套获利大于型住房
由题意知当时,(万元),
即型住房建48套,型住房建32套获得利润最大.
(3)由题意知当时,最大,
即型住房建48套,型住房建32套;
当时,即,三种建房方案获得利润相等;当时,最大,
即型住房建50套,型住房建30套.解:(1)设可制作坚式箱子只,则需型板材张,型板材丂
根据题意,得,解得.
为整数,最多可以做25只坚式箱子.
(2)设制作坚式箱子只,横式箱子只,
根据题意,得,解得.
答:能制作坚式、横式两种无盖箱子分别为5只和30只.
(3)设坚式箱子只,横式箱子只,
则.
且为正整数,为13的整数倍,分类讨论:
(1)当时,,共47只;(2)当时,,共49只.
21世纪教育网(www.21cnjy.com)
第九章一元一次不等式
专题八方程(组)与一元一次不等式组的应用(1)一发现限制条件
01.有若干学生住若干宿舍,如果每间住3人则余8人;如果每间住5人,则最后一间不空也不满,问共有多少学生及多少宿舍
02.某校每年冬季烧煤取暖时间为4个月,如果每月比计划多烧煤,那么取暖用煤总量将超过;如果每月比计划少烧煤,那么取暖用煤总量将不足,该校计划每月烧煤多少吨?
03.某村计划向该村村民提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出15只母羊,若每户发放母羊7只,则有一户可分得母羊,但不足3只.这批种羊共有多少只
04.为庆祝国庆节的到来,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在金山大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来;
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
05.某房地产开发公司计划建两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
(1)该公司对这两种户型住房有哪几种建房方案
(2)该公司所建住房可全部售出,则如何建房获得利润最大
(3)根据市场调查,每套型住房的售价不会改变,每套型住房的售价将会提高万元,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大 (注:利润售价-成本)
成本(万元/套) 25 28
售价(万元/套) 30 34
06.某工厂准备用图甲所示的型正方形板材和型长方形板材,制作成图乙所示的坚式和横式两种无盖箱子.
(1)若该工厂准备用不超过10000元的资金去购买两种型号的板材,并全部制作坚式箱子,已知型板材每张30元,型板材每张90元,求最多可以制作坚式箱子多少只
(2)若该工厂仓库里现有型板材65张,型板材110张,用这批板材制作两种类型的箱子,问制作坚式和横式两种箱子各多少只,恰好将库存的板材用完
(3)若该工厂新购得65张规格为的型正方形板材,将其全部切割成型或型板材(不计损耗),用切割成的板材制作两种类型的箱子,要求坚式箱子不少于20只,且材料恰好用完,则能制作两种箱子共只.
专题八方程(组)与一元一次不等式组的应用(1)一发现限制条件
1.解:设有间宿舍,则有个学生,依题意,得,解得,满足此式的整数等于5或6,因而相应地等于23或26.
答:有23名学生及5间宿舍或26名学生及6间宿舍.
2.解:设该校计划每月烧焟,依题意,得,由(1),得;由(2),得,
故不等式组的解集为,答:该校计划每月烧煠多于而少于.
3.解:设该村共有户,则公羊共有只,母羊共有只,由题意知:解得为整数,,这批种羊共有:(只)
答:这批种羊共有75只.
4.解:(1)设搭配种造型个,则种造型为个.
依题意,得:,解这个不等式组,得:.
是整数,可取可设计三种搭配方案:
(1)种园艺造型31个,种园艺造型19个;(2)种园艺造型32个,种园艺造型18个;(3)种园艺造型33个,种园艺造型17个.
(2)由于种造型的造价成本高于种造型成本,种造型越少,成本越低,
故应选择方案(3)成本最低,最低成本为:(元).
5.解:(1)有三种建房方案:型48套,型32套;
型49套,型31套;型50套,型30套.
(2)设该公司建房获得利润为(万元),
由建房成本和售价表可知,型住房获利:(万元/套);
型住房获利:(万元/套),型住房每套获利大于型住房
由题意知当时,(万元),
即型住房建48套,型住房建32套获得利润最大.
(3)由题意知当时,最大,
即型住房建48套,型住房建32套;
当时,即,三种建房方案获得利润相等;当时,最大,
即型住房建50套,型住房建30套.解:(1)设可制作坚式箱子只,则需型板材张,型板材丂
根据题意,得,解得.
为整数,最多可以做25只坚式箱子.
(2)设制作坚式箱子只,横式箱子只,
根据题意,得,解得.
答:能制作坚式、横式两种无盖箱子分别为5只和30只.
(3)设坚式箱子只,横式箱子只,
则.
且为正整数,为13的整数倍,分类讨论:
(1)当时,,共47只;(2)当时,,共49只.
21世纪教育网(www.21cnjy.com)
