人教版五年级数学上册 第五单元第12课时《实际问题与方程(5)》精品教学方案
文档属性
| 名称 | 人教版五年级数学上册 第五单元第12课时《实际问题与方程(5)》精品教学方案 | 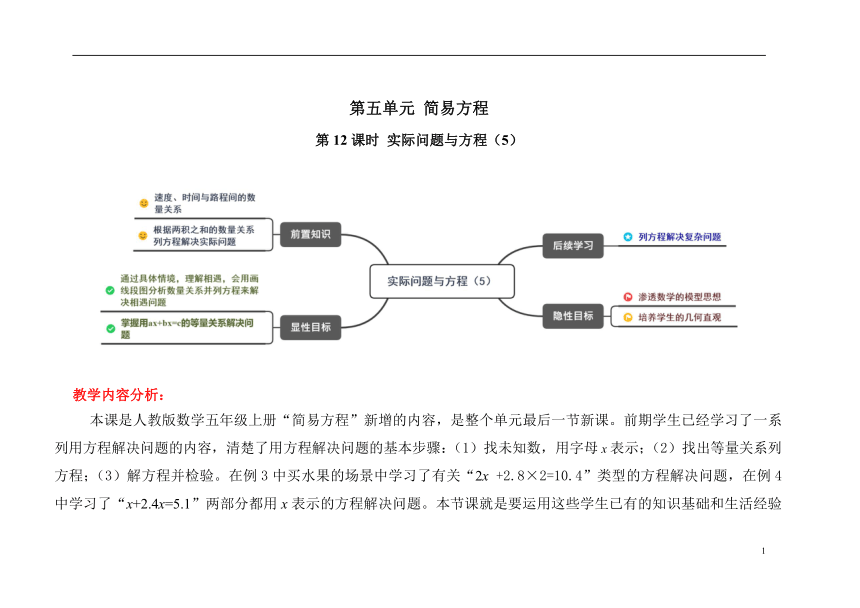 | |
| 格式 | docx | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 15:26:02 | ||
图片预览


文档简介
第五单元 简易方程
第12课时 实际问题与方程(5)
教学内容分析:
本课是人教版数学五年级上册“简易方程”新增的内容,是整个单元最后一节新课。前期学生已经学习了一系列用方程解决问题的内容,清楚了用方程解决问题的基本步骤:(1)找未知数,用字母x表示;(2)找出等量关系列方程;(3)解方程并检验。在例3中买水果的场景中学习了有关“2x +2.8×2=10.4”类型的方程解决问题,在例4中学习了“x+2.4x=5.1”两部分都用x表示的方程解决问题。本节课就是要运用这些学生已有的知识基础和生活经验进行相遇问题的探究,为以后学习用方程解决工作效率、图形的面积等问题打下基础。
教学目标:
1. 在具体的情境中,理解相遇,会用画线段图分析数量关系并列方程来解决相遇问题。
2. 经历用方程解决实际问题的过程中,掌握用ax+bx=c的等量关系解决问题,体会数学的模型思想。
3. 体会用方程解决生活中的问题,感受数学与生活的联系,体验解决问题后的成功感,增强学习数学的自信心。
教学重点:
会用画线段图的方法来分析数量关系并列方程来解决相遇问题。
教学难点:
会用画线段图的方法来分析数量关系。
教学过程:
教学 环节 教师活动 学生活动 设计意图
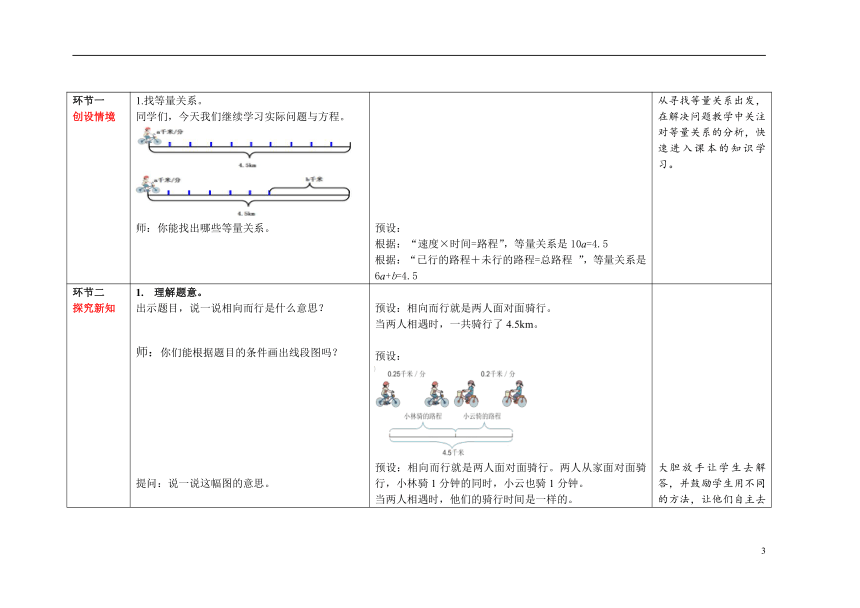
环节一 创设情境 1.找等量关系。 同学们,今天我们继续学习实际问题与方程。 师:你能找出哪些等量关系。 预设: 根据:“速度×时间=路程”,等量关系是10a=4.5 根据:“已行的路程+未行的路程=总路程 ”,等量关系是6a+b=4.5 从寻找等量关系出发,在解决问题教学中关注对等量关系的分析,快速进入课本的知识学习。
环节二 探究新知 理解题意。 出示题目,说一说相向而行是什么意思? 师:你们能根据题目的条件画出线段图吗? 提问:说一说这幅图的意思。 提问:他们俩行驶的路程与两地的距离有着怎样的关系? 师:还可以怎样画线段图? 2.汇报解题方法。 师:怎么列方程解答呢? 提问:还可以怎么解答呢 3.检验结果。 提出问题:怎样检验结果呢? 4.回顾过程。 提出问题:我们刚刚是怎样列方程解决这个问题的? 预设:相向而行就是两人面对面骑行。 当两人相遇时,一共骑行了4.5km。 预设: 预设:相向而行就是两人面对面骑行。两人从家面对面骑行,小林骑1分钟的同时,小云也骑1分钟。 当两人相遇时,他们的骑行时间是一样的。 预设:他们行驶的路程合起来等于总路程。 预设: 预设:小林骑的路程+小云骑的路程=总路程 解:设两人x分钟后相遇。 0.25x+0.2x =4.5 0.45x =4.5 0.45x÷0.45 =4.5÷0.45 x=10 预设:(两人每分钟骑的路程和)×相遇时间 = 总路程 解:设两人 x 分钟后相遇。 (0.25+0.2)x = 4.5 0.45x = 4.5 0.45x÷0.45 = 4.5÷0.45 x=10 预设:检验:小林骑的路程+小云骑的路程 =0.25×10+0.2×10 =4.5(千米)=总路程 检验: (两人每分钟骑的路程和)×相遇时间 =(0.25+0.2)×10 =4.5(千米)=总路程 预设: 先理解题目的意思。 画线段图分析数量关系,知道小林骑的路程+小云骑的路程=总路程。 用速度、时间、路程的数量关系来列方程。 检验作答。 大胆放手让学生去解答,并鼓励学生用不同的方法,让他们自主去探究、去发现,充分发挥学生的主体性,培养学生敢于探索的精神和大胆尝试的能力。
环节三 巩固练习 1.小林家和小云家相距4.5km。小林每分钟骑250m,两人骑自行车从家出发,相向而行。经过10分钟后相遇,小云每分钟骑多少千米? 2.甲、乙两艘轮船同时从上海出发开往青岛。经过18小时后,甲船落后乙船57.6km。甲船每小时行32.5km,乙船每小时行多少千米? 师:同向而行是什么意思? 师:怎么解答? 师:记得检验哦! 预设1:小林骑的路程+小云骑的路程=总路程 解:设小云每分钟骑x km。 250m = 0.25km 0.25×10+10 x = 4.5 2.5+10 x- 2.5= 4.5-2.5 10 x = 2 10 x÷10 = 2÷10 x = 0.2 预设2:(两人每分钟骑的路程和)×相遇时间 解:设小云每分钟骑 x km。 50m = 0.25km (0.25+ x )×10=4.5 (0.25+ x )×10÷10=4.5÷10 0.25+ x =0.45 0. 25+ x- 0.25=0.45-0.25 x = 0.2 预设1:同向而行就是都朝着一个方向行驶。 预设1:解:设乙船每小时行x千米。 18x - 32.5×18=57.6 18x-585+585=57.6+585 18x=642.6 x=35.7 预设2:解:设乙船每小时行x千米。 (x - 32.5)×18=57.6 (x - 32.5)×18÷18=57.6÷18 x - 32.5=3.2 x - 32.5+32.5=3.2+32.5 x= 35.7 在相同的问题情境中,制造新问题,引发学生思考方程的价值,深入理解方程思维的特点。 通过对变式练习,使学生巩固新知,培养学生运用所学知识解决实际问题的能力。
环节四 课堂小结 你有什么收获? 预设1:这类问题的运动时间相同。 预设2:画线段图可以很清楚看出数量间的关系。 预设3:列方程解决问题很有意思,一个等量关系式可以列出不同的方程。 通过回顾与反思,梳理解决问题的步骤。同时,让不同层次的学生谈学习收获,使每个学生都体验到成功的喜悦。
环节五 布置作业 教材P82第11题、第12题
1
第12课时 实际问题与方程(5)
教学内容分析:
本课是人教版数学五年级上册“简易方程”新增的内容,是整个单元最后一节新课。前期学生已经学习了一系列用方程解决问题的内容,清楚了用方程解决问题的基本步骤:(1)找未知数,用字母x表示;(2)找出等量关系列方程;(3)解方程并检验。在例3中买水果的场景中学习了有关“2x +2.8×2=10.4”类型的方程解决问题,在例4中学习了“x+2.4x=5.1”两部分都用x表示的方程解决问题。本节课就是要运用这些学生已有的知识基础和生活经验进行相遇问题的探究,为以后学习用方程解决工作效率、图形的面积等问题打下基础。
教学目标:
1. 在具体的情境中,理解相遇,会用画线段图分析数量关系并列方程来解决相遇问题。
2. 经历用方程解决实际问题的过程中,掌握用ax+bx=c的等量关系解决问题,体会数学的模型思想。
3. 体会用方程解决生活中的问题,感受数学与生活的联系,体验解决问题后的成功感,增强学习数学的自信心。
教学重点:
会用画线段图的方法来分析数量关系并列方程来解决相遇问题。
教学难点:
会用画线段图的方法来分析数量关系。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 1.找等量关系。 同学们,今天我们继续学习实际问题与方程。 师:你能找出哪些等量关系。 预设: 根据:“速度×时间=路程”,等量关系是10a=4.5 根据:“已行的路程+未行的路程=总路程 ”,等量关系是6a+b=4.5 从寻找等量关系出发,在解决问题教学中关注对等量关系的分析,快速进入课本的知识学习。
环节二 探究新知 理解题意。 出示题目,说一说相向而行是什么意思? 师:你们能根据题目的条件画出线段图吗? 提问:说一说这幅图的意思。 提问:他们俩行驶的路程与两地的距离有着怎样的关系? 师:还可以怎样画线段图? 2.汇报解题方法。 师:怎么列方程解答呢? 提问:还可以怎么解答呢 3.检验结果。 提出问题:怎样检验结果呢? 4.回顾过程。 提出问题:我们刚刚是怎样列方程解决这个问题的? 预设:相向而行就是两人面对面骑行。 当两人相遇时,一共骑行了4.5km。 预设: 预设:相向而行就是两人面对面骑行。两人从家面对面骑行,小林骑1分钟的同时,小云也骑1分钟。 当两人相遇时,他们的骑行时间是一样的。 预设:他们行驶的路程合起来等于总路程。 预设: 预设:小林骑的路程+小云骑的路程=总路程 解:设两人x分钟后相遇。 0.25x+0.2x =4.5 0.45x =4.5 0.45x÷0.45 =4.5÷0.45 x=10 预设:(两人每分钟骑的路程和)×相遇时间 = 总路程 解:设两人 x 分钟后相遇。 (0.25+0.2)x = 4.5 0.45x = 4.5 0.45x÷0.45 = 4.5÷0.45 x=10 预设:检验:小林骑的路程+小云骑的路程 =0.25×10+0.2×10 =4.5(千米)=总路程 检验: (两人每分钟骑的路程和)×相遇时间 =(0.25+0.2)×10 =4.5(千米)=总路程 预设: 先理解题目的意思。 画线段图分析数量关系,知道小林骑的路程+小云骑的路程=总路程。 用速度、时间、路程的数量关系来列方程。 检验作答。 大胆放手让学生去解答,并鼓励学生用不同的方法,让他们自主去探究、去发现,充分发挥学生的主体性,培养学生敢于探索的精神和大胆尝试的能力。
环节三 巩固练习 1.小林家和小云家相距4.5km。小林每分钟骑250m,两人骑自行车从家出发,相向而行。经过10分钟后相遇,小云每分钟骑多少千米? 2.甲、乙两艘轮船同时从上海出发开往青岛。经过18小时后,甲船落后乙船57.6km。甲船每小时行32.5km,乙船每小时行多少千米? 师:同向而行是什么意思? 师:怎么解答? 师:记得检验哦! 预设1:小林骑的路程+小云骑的路程=总路程 解:设小云每分钟骑x km。 250m = 0.25km 0.25×10+10 x = 4.5 2.5+10 x- 2.5= 4.5-2.5 10 x = 2 10 x÷10 = 2÷10 x = 0.2 预设2:(两人每分钟骑的路程和)×相遇时间 解:设小云每分钟骑 x km。 50m = 0.25km (0.25+ x )×10=4.5 (0.25+ x )×10÷10=4.5÷10 0.25+ x =0.45 0. 25+ x- 0.25=0.45-0.25 x = 0.2 预设1:同向而行就是都朝着一个方向行驶。 预设1:解:设乙船每小时行x千米。 18x - 32.5×18=57.6 18x-585+585=57.6+585 18x=642.6 x=35.7 预设2:解:设乙船每小时行x千米。 (x - 32.5)×18=57.6 (x - 32.5)×18÷18=57.6÷18 x - 32.5=3.2 x - 32.5+32.5=3.2+32.5 x= 35.7 在相同的问题情境中,制造新问题,引发学生思考方程的价值,深入理解方程思维的特点。 通过对变式练习,使学生巩固新知,培养学生运用所学知识解决实际问题的能力。
环节四 课堂小结 你有什么收获? 预设1:这类问题的运动时间相同。 预设2:画线段图可以很清楚看出数量间的关系。 预设3:列方程解决问题很有意思,一个等量关系式可以列出不同的方程。 通过回顾与反思,梳理解决问题的步骤。同时,让不同层次的学生谈学习收获,使每个学生都体验到成功的喜悦。
环节五 布置作业 教材P82第11题、第12题
1
