人教版五年级数学下册 最大公因数示范教学方案
文档属性
| 名称 | 人教版五年级数学下册 最大公因数示范教学方案 |

|
|
| 格式 | doc | ||
| 文件大小 | 578.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:00:45 | ||
图片预览


文档简介
最大公因数
教学目标:
1.理解公因数和最大公因数的意义,理解因数、公因数和最大公因数的区别和联系。
2.掌握求两个数最大公因数的方法,会选择合适的方法正确的求两个数的最大公因数。
3.经历探究求两个数最大公因数方法的过程,培养学生分析、归纳等思维能力。激发学生自主学习、积极探索和合作交流的良好习惯。
教学重点:
理解公因数和最大公因数的意义。
教学难点:
利用公因数、最大公因数解决简单的实际问题。
教学过程:
一、新课导入
师:同学们,我们在第二章学过因数、质数与合数,你还记得吗?
生:(1)一个数的最小因数是(1),最大因数是(它本身)。
(2)一个数,只有1和它本身2个因数,这样的数叫做(质数)。一个数,除了1和它本身两个因数,还有其他的因数,这样的数叫做(合数)。
师:怎样找一个数的因数呢?
生:用这个数依次除以1、2、3、4……如果商是整数,那么除数和商都是这个数的因数。
师:今天我们就来继续学习因数的有关知识。
设计意图:通过复习引入,不仅能对旧知进行复习,还能将所学知识迁移到本节课,为新知学习奠定基础。
二、探究新知
1.认识公因数和最大公因数。
出示:8和12的公有的因数是哪几个?公有的最大因数是多少?
师:你的思考过程是怎样的?
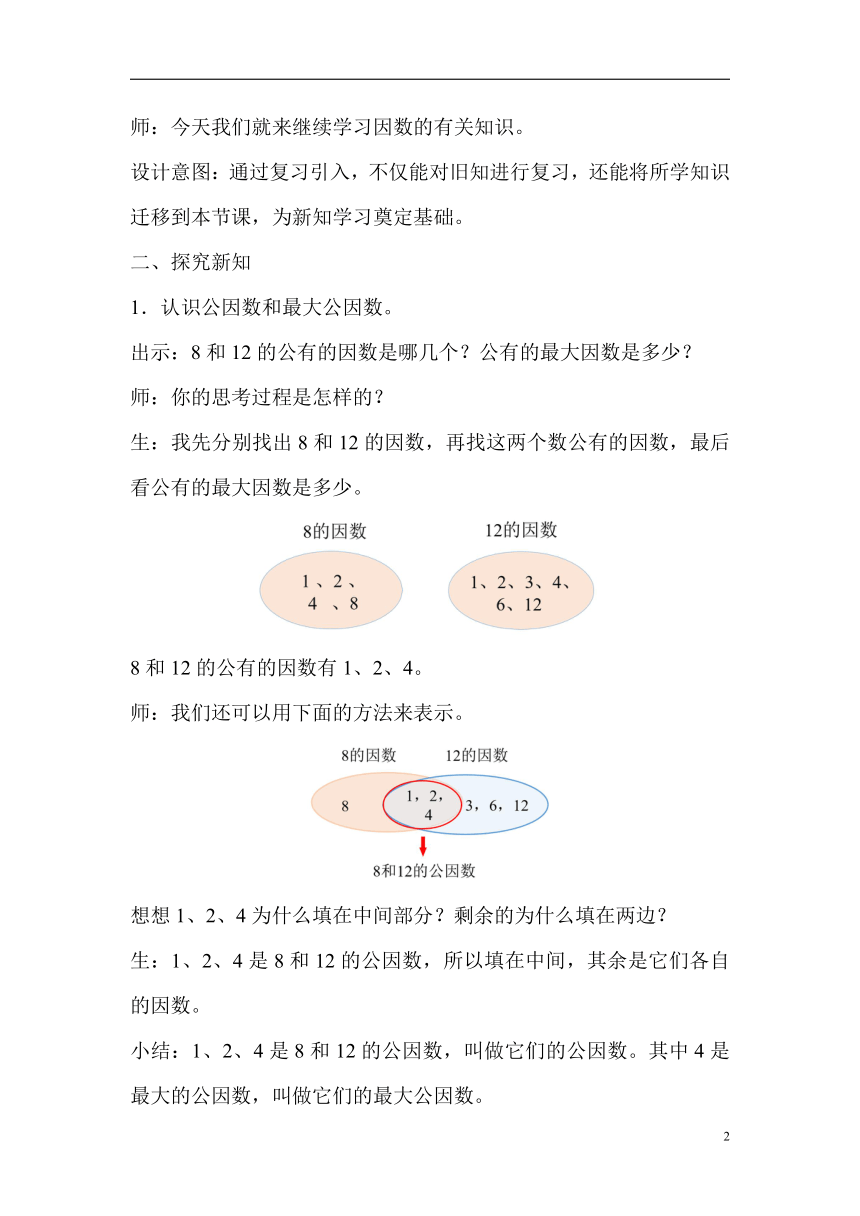
生:我先分别找出8和12的因数,再找这两个数公有的因数,最后看公有的最大因数是多少。
8和12的公有的因数有1、2、4。
师:我们还可以用下面的方法来表示。
想想1、2、4为什么填在中间部分?剩余的为什么填在两边?
生:1、2、4是8和12的公因数,所以填在中间,其余是它们各自的因数。
小结:1、2、4是8和12的公因数,叫做它们的公因数。其中4是最大的公因数,叫做它们的最大公因数。
出示:怎样求18和27的最大公因数?
师:说说你的思考过程是怎样的?
生1:我先找出18的因数有1、2、3、6、9、18,再找出27的因数有1、3、9、27。18和27的公因数有1、3、9,其中最大的一个是9,所以18和27的最大公因数是9。
生2:我看18的因数中哪些是27的因数,发现18的因数中1、3、9也是27的因数。18和27的最大公因数是9。
师:你还有其他方法吗?和同学们讨论一下。
生3:利用分解质因数法,可以比较简便地求出两个数的最大公因数。
18=2×3×3 27=3×3×3
18和27的最大公因数:3×3=9。
生4:为了简便,还可以把分解质因数法写成短除法的形式。
18和27的最大公因数是3×3=9。
师:通过学习,你了解求几个数的最大公因数的方法了吗?
注:这两个图片是动画缩略图,通过小游戏完成求两个数最大公因数的练习,掌握求两个数最大公因数的方法。如需使用此资源,请插入动画“【数学探究】求最大公因数练习”。
设计意图:本部分内容以前有基础,并不是特别困难。
2.解决问题。
出示:小明家的储藏室长16 dm,宽12 dm,如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
(1)阅读与理解:根据题目,你知道了哪些信息?
生:贮藏室的长16 dm,宽12 dm。要用多少整块边长是整分米数的正方形地砖把贮藏室的地面铺满?
(2)分析与解答
生1:要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
生2:只要找出16和12的公因数,就可以知道选择边长是几分米的地砖了。
16和12的公因数有1、2、4,其中最大公因数是4。
所以可以选边长是1 dm、2 dm、4 dm的正方形地砖,边长最大是4 dm。
(3)回顾与反思
师:边长为1 dm、2 dm、4 dm的正方形地砖在储藏室的长、宽上都是整数块吗?
生:可以在长方形纸上画一画来验证。
通过画图可以看出,可以选边长是1 dm、2 dm、4 dm的正方形地砖,边长最大是4 dm。
设计意图:通过将知识应用在解决问题上,不仅培养学生的解决问题的能力,还能使学生认识到数学知识对于生活的重要性。
三、巩固练习
1.找出下面每组数的最大公因数。
6和9 15和12 42和54 30和45 99和36
5和9 34和17 16和48 15和16 13和78
解析:最大公因数是两个数公有的因数中最大的一个。
答案:3 3 6 15 9 1 17 16 1 13
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
2.在相应的括号里写出相邻阶梯上两个数的最大公因数。
解析:最大公因数是两个数公有的因数中最大的一个。
答案:
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
3.有一张长方形纸,长70 cm,宽50 cm。如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是几厘米?
解析:正方形的边长是长方形纸长和宽的公因数,长方形纸才能要剪成若干同样大小的正方形而没有剩余。
答案:50的因数有:1、2、5、10、25、50;
70的因数有:1、2、5、7、10、14、35、70;
50和70的最大公因数是10。
答:剪出的小正方形的边长最大是10厘米。
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
四、课堂小结
两个数公有的因数叫做它们的公因数,其中最大的一个叫做它们的最大公因数。
设计意图:通过课堂小结,巩固本节课所学内容,帮助学生构建知识体系。
1
教学目标:
1.理解公因数和最大公因数的意义,理解因数、公因数和最大公因数的区别和联系。
2.掌握求两个数最大公因数的方法,会选择合适的方法正确的求两个数的最大公因数。
3.经历探究求两个数最大公因数方法的过程,培养学生分析、归纳等思维能力。激发学生自主学习、积极探索和合作交流的良好习惯。
教学重点:
理解公因数和最大公因数的意义。
教学难点:
利用公因数、最大公因数解决简单的实际问题。
教学过程:
一、新课导入
师:同学们,我们在第二章学过因数、质数与合数,你还记得吗?
生:(1)一个数的最小因数是(1),最大因数是(它本身)。
(2)一个数,只有1和它本身2个因数,这样的数叫做(质数)。一个数,除了1和它本身两个因数,还有其他的因数,这样的数叫做(合数)。
师:怎样找一个数的因数呢?
生:用这个数依次除以1、2、3、4……如果商是整数,那么除数和商都是这个数的因数。
师:今天我们就来继续学习因数的有关知识。
设计意图:通过复习引入,不仅能对旧知进行复习,还能将所学知识迁移到本节课,为新知学习奠定基础。
二、探究新知
1.认识公因数和最大公因数。
出示:8和12的公有的因数是哪几个?公有的最大因数是多少?
师:你的思考过程是怎样的?
生:我先分别找出8和12的因数,再找这两个数公有的因数,最后看公有的最大因数是多少。
8和12的公有的因数有1、2、4。
师:我们还可以用下面的方法来表示。
想想1、2、4为什么填在中间部分?剩余的为什么填在两边?
生:1、2、4是8和12的公因数,所以填在中间,其余是它们各自的因数。
小结:1、2、4是8和12的公因数,叫做它们的公因数。其中4是最大的公因数,叫做它们的最大公因数。
出示:怎样求18和27的最大公因数?
师:说说你的思考过程是怎样的?
生1:我先找出18的因数有1、2、3、6、9、18,再找出27的因数有1、3、9、27。18和27的公因数有1、3、9,其中最大的一个是9,所以18和27的最大公因数是9。
生2:我看18的因数中哪些是27的因数,发现18的因数中1、3、9也是27的因数。18和27的最大公因数是9。
师:你还有其他方法吗?和同学们讨论一下。
生3:利用分解质因数法,可以比较简便地求出两个数的最大公因数。
18=2×3×3 27=3×3×3
18和27的最大公因数:3×3=9。
生4:为了简便,还可以把分解质因数法写成短除法的形式。
18和27的最大公因数是3×3=9。
师:通过学习,你了解求几个数的最大公因数的方法了吗?
注:这两个图片是动画缩略图,通过小游戏完成求两个数最大公因数的练习,掌握求两个数最大公因数的方法。如需使用此资源,请插入动画“【数学探究】求最大公因数练习”。
设计意图:本部分内容以前有基础,并不是特别困难。
2.解决问题。
出示:小明家的储藏室长16 dm,宽12 dm,如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
(1)阅读与理解:根据题目,你知道了哪些信息?
生:贮藏室的长16 dm,宽12 dm。要用多少整块边长是整分米数的正方形地砖把贮藏室的地面铺满?
(2)分析与解答
生1:要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
生2:只要找出16和12的公因数,就可以知道选择边长是几分米的地砖了。
16和12的公因数有1、2、4,其中最大公因数是4。
所以可以选边长是1 dm、2 dm、4 dm的正方形地砖,边长最大是4 dm。
(3)回顾与反思
师:边长为1 dm、2 dm、4 dm的正方形地砖在储藏室的长、宽上都是整数块吗?
生:可以在长方形纸上画一画来验证。
通过画图可以看出,可以选边长是1 dm、2 dm、4 dm的正方形地砖,边长最大是4 dm。
设计意图:通过将知识应用在解决问题上,不仅培养学生的解决问题的能力,还能使学生认识到数学知识对于生活的重要性。
三、巩固练习
1.找出下面每组数的最大公因数。
6和9 15和12 42和54 30和45 99和36
5和9 34和17 16和48 15和16 13和78
解析:最大公因数是两个数公有的因数中最大的一个。
答案:3 3 6 15 9 1 17 16 1 13
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
2.在相应的括号里写出相邻阶梯上两个数的最大公因数。
解析:最大公因数是两个数公有的因数中最大的一个。
答案:
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
3.有一张长方形纸,长70 cm,宽50 cm。如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是几厘米?
解析:正方形的边长是长方形纸长和宽的公因数,长方形纸才能要剪成若干同样大小的正方形而没有剩余。
答案:50的因数有:1、2、5、10、25、50;
70的因数有:1、2、5、7、10、14、35、70;
50和70的最大公因数是10。
答:剪出的小正方形的边长最大是10厘米。
设计意图:本题是对求最大公因数的方法的巩固练习,使学生更熟练得掌握求最大公因数的方法。
四、课堂小结
两个数公有的因数叫做它们的公因数,其中最大的一个叫做它们的最大公因数。
设计意图:通过课堂小结,巩固本节课所学内容,帮助学生构建知识体系。
1
