人教版八年级下册数学18.1.2 平行四边形的判定(第1课时)课件(共18张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.2 平行四边形的判定(第1课时)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 14:35:38 | ||
图片预览





文档简介
(共18张PPT)
八年级数学下(RJ)
18.1.2 平行四边形的判定
第一课时
情景导入
中原第一峰
思考
情景导入
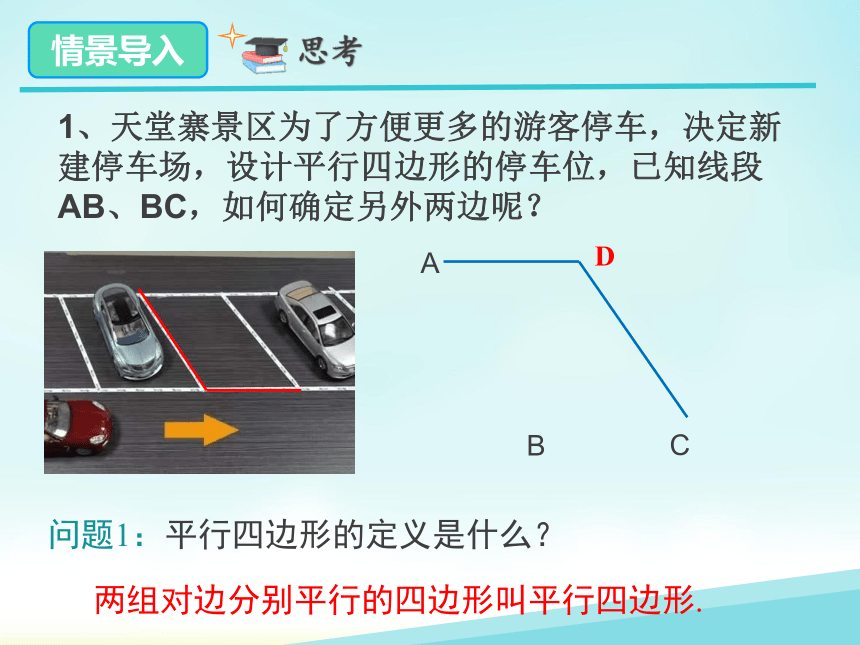
1、天堂寨景区为了方便更多的游客停车,决定新建停车场,设计平行四边形的停车位,已知线段AB、BC,如何确定另外两边呢?
A
B
C
问题1:平行四边形的定义是什么?
两组对边分别平行的四边形叫平行四边形.
D
回顾旧知
B
O
D
A
C
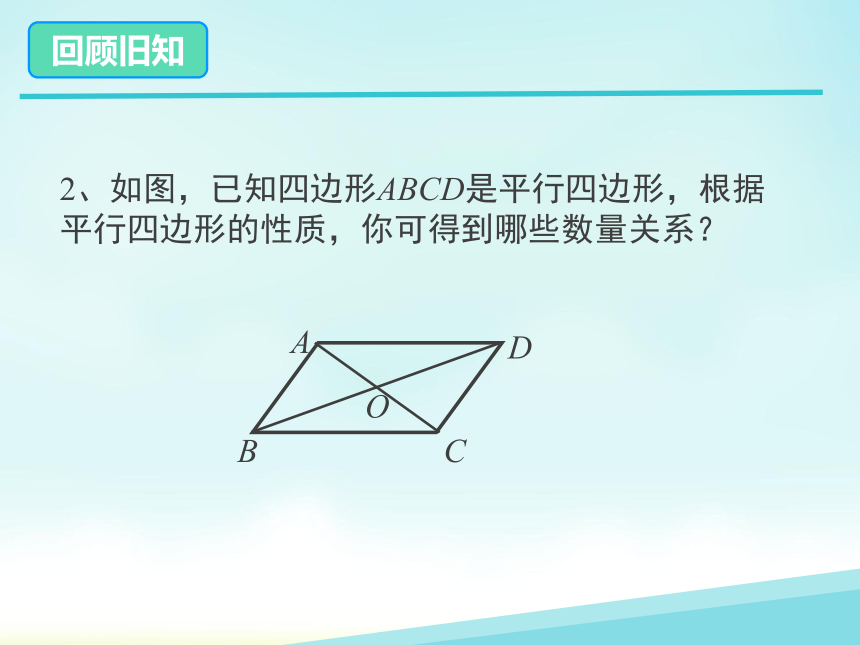
2、如图,已知四边形ABCD是平行四边形,根据平行四边形的性质,你可得到哪些数量关系?
新知探究
一
揭榜赛
3、小组讨论并且猜想:选择哪两个条件可以判定四边形ABCD是平行四边形?
①AB=DC
②AD=BC
③∠A=∠C
④∠B=∠D
⑤OA=OC
⑥OB=OD
B
O
D
A
C
猜想1:两组对边分别相等的四边形是平行四边形。
新知探究
一
猜想2:两组对角分别相等的四边形是平行四边形。
猜想3:对角线互相平分的四边形是平行四边形。
B
O
D
A
C
已知:
求证:
四边形ABCD中,AB=DC,AD=BC。
四边形ABCD是平行四边形。
已知:
求证:
四边形ABCD中,∠A=∠C,∠B=∠D。
四边形ABCD是平行四边形。
已知:
求证:
四边形ABCD中,OA=OC,OB=OD。
四边形ABCD是平行四边形。
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形;
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结1
两组对边分别相等的四边形是平行四边形。
几何语言描述:
B
D
A
C
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形。
定理1:
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形;
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结2
两组对边分别相等的四边形是平行四边形。
定理1:
几何语言描述:
B
D
A
C
定理1:
定理2:
在四边形ABCD中,∵∠A=∠C,∠B=∠D。
∴四边形ABCD是平行四边形。
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形。
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结3
两组对边分别相等的四边形是平行四边形。
定理1:
定理2:
定理3:
几何语言描述:
B
O
D
A
C
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形。
归纳总结
对角线互相平分的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
小试牛刀
例1 如图, □ABCD 的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形。
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
典例精析
二
变式:若E、F继续移动至OA、OC的延长线上,仍使AE=CF,则BFDE还是平行四边形吗 为什么
解:四边形BFDE是平行四边形,理由如下:
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF
即EO=FO
又∵BO=DO
∴四边形BFDE是平行四边形
变式训练
轻松一刻
判断对错(希沃白板做游戏,两组同学比赛完成)
两组对边分别相等的四边形是平行四边形。 ( )
两条对角线互相平分的四边形是平行四边形。( )
一组对边平行的四边形是平行四边形。 ( )
两条对角线相等的四边形是平行四边形。 ( )
两组对角分别相等的四边形是平行四边形。 ( )
课堂小结
这节课你有什么收获呢?
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课后作业
1.根据下列条件,不能判定四边形为平行四边形的是
( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
必做题
课后作业
3.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
必做题
如图,在□ ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
求证:四边形AFCE是平行四边形.
选做题
课后作业
八年级数学下(RJ)
18.1.2 平行四边形的判定
第一课时
情景导入
中原第一峰
思考
情景导入
1、天堂寨景区为了方便更多的游客停车,决定新建停车场,设计平行四边形的停车位,已知线段AB、BC,如何确定另外两边呢?
A
B
C
问题1:平行四边形的定义是什么?
两组对边分别平行的四边形叫平行四边形.
D
回顾旧知
B
O
D
A
C
2、如图,已知四边形ABCD是平行四边形,根据平行四边形的性质,你可得到哪些数量关系?
新知探究
一
揭榜赛
3、小组讨论并且猜想:选择哪两个条件可以判定四边形ABCD是平行四边形?
①AB=DC
②AD=BC
③∠A=∠C
④∠B=∠D
⑤OA=OC
⑥OB=OD
B
O
D
A
C
猜想1:两组对边分别相等的四边形是平行四边形。
新知探究
一
猜想2:两组对角分别相等的四边形是平行四边形。
猜想3:对角线互相平分的四边形是平行四边形。
B
O
D
A
C
已知:
求证:
四边形ABCD中,AB=DC,AD=BC。
四边形ABCD是平行四边形。
已知:
求证:
四边形ABCD中,∠A=∠C,∠B=∠D。
四边形ABCD是平行四边形。
已知:
求证:
四边形ABCD中,OA=OC,OB=OD。
四边形ABCD是平行四边形。
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形;
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结1
两组对边分别相等的四边形是平行四边形。
几何语言描述:
B
D
A
C
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形。
定理1:
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形;
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结2
两组对边分别相等的四边形是平行四边形。
定理1:
几何语言描述:
B
D
A
C
定理1:
定理2:
在四边形ABCD中,∵∠A=∠C,∠B=∠D。
∴四边形ABCD是平行四边形。
猜想1:
猜想2:两组对角分别相等的四边形是平行四边形。
猜想3:对角线互相平分的四边形是平行四边形。
归纳总结3
两组对边分别相等的四边形是平行四边形。
定理1:
定理2:
定理3:
几何语言描述:
B
O
D
A
C
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形。
归纳总结
对角线互相平分的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
小试牛刀
例1 如图, □ABCD 的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形。
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
典例精析
二
变式:若E、F继续移动至OA、OC的延长线上,仍使AE=CF,则BFDE还是平行四边形吗 为什么
解:四边形BFDE是平行四边形,理由如下:
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF
即EO=FO
又∵BO=DO
∴四边形BFDE是平行四边形
变式训练
轻松一刻
判断对错(希沃白板做游戏,两组同学比赛完成)
两组对边分别相等的四边形是平行四边形。 ( )
两条对角线互相平分的四边形是平行四边形。( )
一组对边平行的四边形是平行四边形。 ( )
两条对角线相等的四边形是平行四边形。 ( )
两组对角分别相等的四边形是平行四边形。 ( )
课堂小结
这节课你有什么收获呢?
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课后作业
1.根据下列条件,不能判定四边形为平行四边形的是
( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
必做题
课后作业
3.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
必做题
如图,在□ ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
求证:四边形AFCE是平行四边形.
选做题
课后作业
