人教版九年级上册数学21.2.4一元二次方程根与系数的关系课件(共12张PPT)
文档属性
| 名称 | 人教版九年级上册数学21.2.4一元二次方程根与系数的关系课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 14:43:11 | ||
图片预览




文档简介
(共12张PPT)
21.2.4 一元二次方程的根与系数的关系
韦达,1540 年出生于法国的波亚图,他把符号系统引入代数学,对数学的发展发挥了巨大的作用,人们为了纪念他在代数学上的功绩,称他为“代数学之父” .
x+y=8
x=7
s=vt
a=b-10
y=3x+4
a+b=3
a2+b2=c2
导入新课
-4
1
2
3
-1
-3
-4
5
6
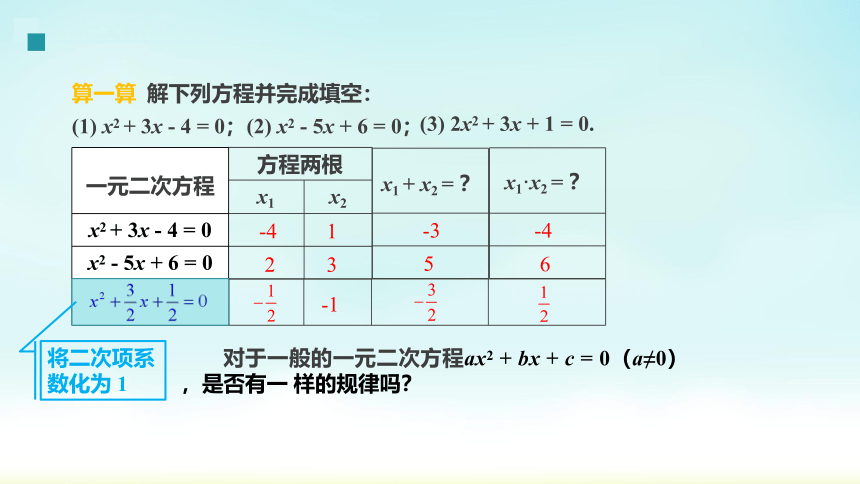
(1) x2 + 3x - 4 = 0;(2) x2 - 5x + 6 = 0;
算一算 解下列方程并完成填空:
x1 + x2 = ?
x1·x2 = ?
2x2 + 3x + 1 = 0
方程两根
x1 x2
一元二次方程
x2 + 3x - 4 = 0
x2 - 5x + 6 = 0
(3) 2x2 + 3x + 1 = 0.
将二次项系数化为 1
对于一般的一元二次方程ax2 + bx + c = 0(a≠0),是否有一 样的规律吗?
讲授新课
如何求出一般的一元二次方程 ax2 + bx + c = 0 (a ≠ 0) 两根之积、两根之和?
思考探究
有实数根的前提是什么呢?
Δ=b2-4ac≥0
讲授新课
对于方程ax2+bx+c=0(a≠0) ,当Δ≥0时,设ax2+bx+c=0(a≠0)的两个根为x1,x2,此时x1+x2,x1·x2等于多少呢?
探究结论
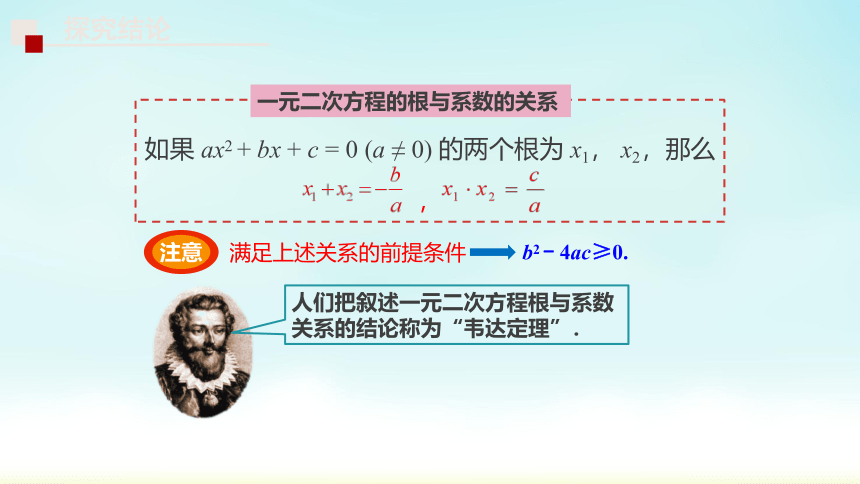
如果 ax2 + bx + c = 0 (a ≠ 0) 的两个根为 x1, x2,那么
,
注意
满足上述关系的前提条件
b2 - 4ac≥0.
一元二次方程的根与系数的关系
人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”.
探究结论
例1 不解方程,求下列方程的两根之和、两根之积.
(1)x2 – 6x – 15 = 0;(2) 5x – 1 = 4x2
(1)解: a = 1,b = – 6, c = – 15.
(2)解:整理方程得:4x2-5x+1=0
Δ = b2 - 4ac
= ( – 6 )2 – 4 × 1 ×(– 15 )
= 96 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么x1 + x2 = – ( – 6 ) =6,
x1 x2 = - 15.
先化为一般式
定理应用
a = 4,b = – 5, c = 1.
Δ = b2 - 4ac
= ( – 5 )2 – 4 × (– 5 ) ×1 = 45 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么 x1 + x2 = , x1 x2 = .
练习1 不解方程,求下列方程的两根之和、两根之积.
(1)3x2 + 7x - 9 = 0;(2) 2x2-4x +9 =0.
(2)解:a = 2,b = - 4,c = 9.
Δ = b2 - 4ac
= (-4)2 – 4 ×2×9 = -56 < 0.
∴方程无实数根.
(1)解:a = 3,b = 7, c = - 9.
Δ = b2 - 4ac
= 72 – 4 ×3×(-9) = 157 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么 x1 + x2 = , x1 x2 = -3.
定理应用
例2 设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,则
(1)x1 + x2 = ,x1·x2 = .
(x1+x2)2 – 2x1x2
∴原式=42 – 2×1
=14
4
1
(x1 + 1)(x2 + 1)=
(2)求下列式子的值:
x12+ x22 =
x1x2+(x1+x2)+1
∴原式=1+4+1
=6
定理应用
∵x1+x2=4,x1x2=1
∵x1+x2=4,x1x2=1
∴原式
∵x1+x2=4,x1x2=1
x1 + x2 = 4 ,x1·x2 = 1
变式 设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,求下列式子的值:
(x1- x2)2
定理应用
一元二次方程的根与系数的关系
内 容
应 用
如果一元二次方程 ax2 + bx + c = 0 (a ≠ 0) 的两个根分别是 x1,x2,那么
,
课堂小结
……
(x1 + 1)(x2 + 1)
x12+ x22
(x1- x2)2
思考题:
当 k 为何值时,方程 2x2 - kx + 1 = 0 的两根之差为 1?
必做题:
1.教材P16练习;
2.教材P17复习巩固第7题;
3.教材P25复习巩固第4题.
常思常悟
课后作业
21.2.4 一元二次方程的根与系数的关系
韦达,1540 年出生于法国的波亚图,他把符号系统引入代数学,对数学的发展发挥了巨大的作用,人们为了纪念他在代数学上的功绩,称他为“代数学之父” .
x+y=8
x=7
s=vt
a=b-10
y=3x+4
a+b=3
a2+b2=c2
导入新课
-4
1
2
3
-1
-3
-4
5
6
(1) x2 + 3x - 4 = 0;(2) x2 - 5x + 6 = 0;
算一算 解下列方程并完成填空:
x1 + x2 = ?
x1·x2 = ?
2x2 + 3x + 1 = 0
方程两根
x1 x2
一元二次方程
x2 + 3x - 4 = 0
x2 - 5x + 6 = 0
(3) 2x2 + 3x + 1 = 0.
将二次项系数化为 1
对于一般的一元二次方程ax2 + bx + c = 0(a≠0),是否有一 样的规律吗?
讲授新课
如何求出一般的一元二次方程 ax2 + bx + c = 0 (a ≠ 0) 两根之积、两根之和?
思考探究
有实数根的前提是什么呢?
Δ=b2-4ac≥0
讲授新课
对于方程ax2+bx+c=0(a≠0) ,当Δ≥0时,设ax2+bx+c=0(a≠0)的两个根为x1,x2,此时x1+x2,x1·x2等于多少呢?
探究结论
如果 ax2 + bx + c = 0 (a ≠ 0) 的两个根为 x1, x2,那么
,
注意
满足上述关系的前提条件
b2 - 4ac≥0.
一元二次方程的根与系数的关系
人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”.
探究结论
例1 不解方程,求下列方程的两根之和、两根之积.
(1)x2 – 6x – 15 = 0;(2) 5x – 1 = 4x2
(1)解: a = 1,b = – 6, c = – 15.
(2)解:整理方程得:4x2-5x+1=0
Δ = b2 - 4ac
= ( – 6 )2 – 4 × 1 ×(– 15 )
= 96 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么x1 + x2 = – ( – 6 ) =6,
x1 x2 = - 15.
先化为一般式
定理应用
a = 4,b = – 5, c = 1.
Δ = b2 - 4ac
= ( – 5 )2 – 4 × (– 5 ) ×1 = 45 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么 x1 + x2 = , x1 x2 = .
练习1 不解方程,求下列方程的两根之和、两根之积.
(1)3x2 + 7x - 9 = 0;(2) 2x2-4x +9 =0.
(2)解:a = 2,b = - 4,c = 9.
Δ = b2 - 4ac
= (-4)2 – 4 ×2×9 = -56 < 0.
∴方程无实数根.
(1)解:a = 3,b = 7, c = - 9.
Δ = b2 - 4ac
= 72 – 4 ×3×(-9) = 157 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2,
那么 x1 + x2 = , x1 x2 = -3.
定理应用
例2 设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,则
(1)x1 + x2 = ,x1·x2 = .
(x1+x2)2 – 2x1x2
∴原式=42 – 2×1
=14
4
1
(x1 + 1)(x2 + 1)=
(2)求下列式子的值:
x12+ x22 =
x1x2+(x1+x2)+1
∴原式=1+4+1
=6
定理应用
∵x1+x2=4,x1x2=1
∵x1+x2=4,x1x2=1
∴原式
∵x1+x2=4,x1x2=1
x1 + x2 = 4 ,x1·x2 = 1
变式 设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,求下列式子的值:
(x1- x2)2
定理应用
一元二次方程的根与系数的关系
内 容
应 用
如果一元二次方程 ax2 + bx + c = 0 (a ≠ 0) 的两个根分别是 x1,x2,那么
,
课堂小结
……
(x1 + 1)(x2 + 1)
x12+ x22
(x1- x2)2
思考题:
当 k 为何值时,方程 2x2 - kx + 1 = 0 的两根之差为 1?
必做题:
1.教材P16练习;
2.教材P17复习巩固第7题;
3.教材P25复习巩固第4题.
常思常悟
课后作业
同课章节目录
