6.2.2排列数 课件(共19张PPT)
文档属性
| 名称 | 6.2.2排列数 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 362.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 11:38:11 | ||
图片预览






文档简介
(共19张PPT)
6.2.2 排 列 数
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性
(2) 元素的有序性
判断关键是看选出的元素有没有顺序要求。
温故而知新:
3、排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,它不是一个数;
个元素
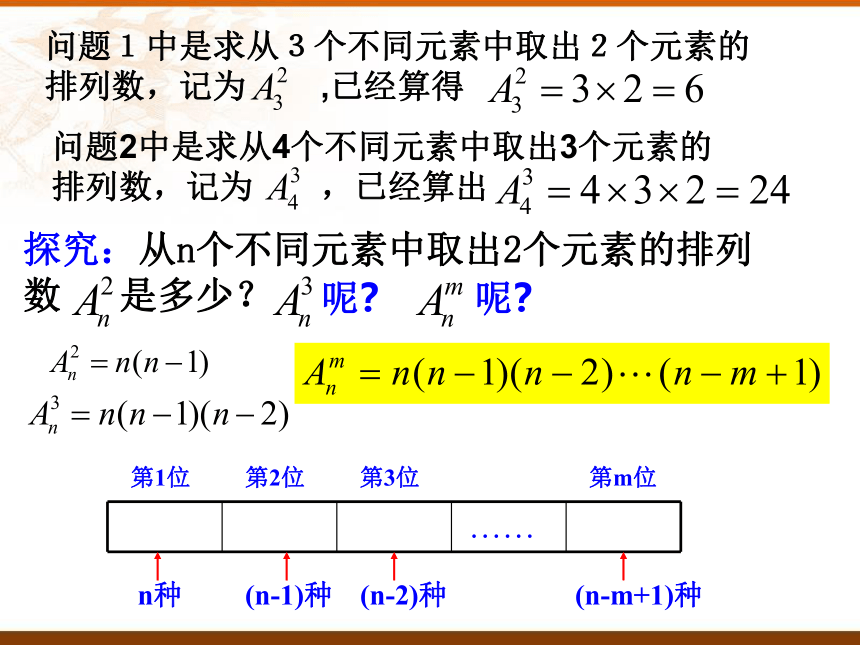
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
特别地,我们把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列.
将n个不同的元素全部取出的排列数,等于正整数1到n的连乘积.正整数1到n的连乘积,叫做n的阶乘,用n!表示.于是,n个元素的全排列数公式可以写成
我们规定,0!=1
追问1:你能写一下常见自然数的阶乘吗?
1!=1;
2!=2×1=2
3!=3×2×1=6
4!=4×3×2×1=24
例3:计算:
思考:由例3可以看到
观察这两个结果,从中你发现它们的共性吗?
解:根据排列数公式,可得:
思考:由例3可以看到
观察这两个结果,从中你发现它们的共性吗?
排列数公式
的阶乘形式
排列数公式
的连乘形式
排列数公式1:
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
排列数公式2:
为了使当m=n时上面的公式也成立,规定:
例4:用0到9这10个数字,可以组成多少个没有重复数字的三位数?
百位
十位
个位
解法一:
解法二:对排列方法分类思考。符合条件的三位数可分为三类:
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
根据分类加法计数原理
特殊元素优先考虑
对排列方法分步思考
特殊位置优先安排
2.排列数公式:
1.排列数的定义和表示:
3.n个元素的全排列数公式:
0!=1
把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
4.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
课堂小结:
请看课本P20:练习3
1.用0-5这六个数字可以组成没有重复数字的
(1)四位偶数有多少个?奇数?
(5)十位数比个位数大的三位数?
(2)能被5整除的四位数有多少?
(3)能被3整除的四位数有多少?
(4)能被25整除的四位数有多少?
(6)能组成多少个比240135大的数?若把组成的全部六位数从小到大排列起来,那么240135是第几个数?
学以致用:
2. 8人围桌而坐,共有多少种坐法
学以致用:
3.三个女生和五个男生排在一排.
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
学以致用:
捆绑法
插空法
排队问题的相邻、不相邻问题
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.
4.分别求出符合下列要求的不同排法的种数.
(1)6名学生排3排,前排1人,中排2人,后排3人;
(2)6名学生排成一排,甲不在排头也不在排尾;
(3)6人排成一排,甲、乙不相邻.
3.三个女生和五个男生排在一排.
(3)如果两端都不能排女生,可有多少种不同的排法?
学以致用:
排队问题的相邻、不相邻、定序等问题
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.
5.用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复数字的数?
(1)六位数且是奇数;
(2)个位上的数字不是5的六位数;
(3)不大于4 310的四位数且是偶数.
学以致用:
6.用0,1,2,…,9十个数字可组成多少个满足以下条件的没有重复数字的数?
(1)五位奇数;
(2)大于30 000的五位偶数.
学以致用:
7.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )
A.144个 B.120个 C.96个 D.72个
B
学以致用:
8.六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________
24
学以致用:
6.2.2 排 列 数
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性
(2) 元素的有序性
判断关键是看选出的元素有没有顺序要求。
温故而知新:
3、排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,它不是一个数;
个元素
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
特别地,我们把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列.
将n个不同的元素全部取出的排列数,等于正整数1到n的连乘积.正整数1到n的连乘积,叫做n的阶乘,用n!表示.于是,n个元素的全排列数公式可以写成
我们规定,0!=1
追问1:你能写一下常见自然数的阶乘吗?
1!=1;
2!=2×1=2
3!=3×2×1=6
4!=4×3×2×1=24
例3:计算:
思考:由例3可以看到
观察这两个结果,从中你发现它们的共性吗?
解:根据排列数公式,可得:
思考:由例3可以看到
观察这两个结果,从中你发现它们的共性吗?
排列数公式
的阶乘形式
排列数公式
的连乘形式
排列数公式1:
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
排列数公式2:
为了使当m=n时上面的公式也成立,规定:
例4:用0到9这10个数字,可以组成多少个没有重复数字的三位数?
百位
十位
个位
解法一:
解法二:对排列方法分类思考。符合条件的三位数可分为三类:
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
根据分类加法计数原理
特殊元素优先考虑
对排列方法分步思考
特殊位置优先安排
2.排列数公式:
1.排列数的定义和表示:
3.n个元素的全排列数公式:
0!=1
把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
4.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
课堂小结:
请看课本P20:练习3
1.用0-5这六个数字可以组成没有重复数字的
(1)四位偶数有多少个?奇数?
(5)十位数比个位数大的三位数?
(2)能被5整除的四位数有多少?
(3)能被3整除的四位数有多少?
(4)能被25整除的四位数有多少?
(6)能组成多少个比240135大的数?若把组成的全部六位数从小到大排列起来,那么240135是第几个数?
学以致用:
2. 8人围桌而坐,共有多少种坐法
学以致用:
3.三个女生和五个男生排在一排.
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
学以致用:
捆绑法
插空法
排队问题的相邻、不相邻问题
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.
4.分别求出符合下列要求的不同排法的种数.
(1)6名学生排3排,前排1人,中排2人,后排3人;
(2)6名学生排成一排,甲不在排头也不在排尾;
(3)6人排成一排,甲、乙不相邻.
3.三个女生和五个男生排在一排.
(3)如果两端都不能排女生,可有多少种不同的排法?
学以致用:
排队问题的相邻、不相邻、定序等问题
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.
5.用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复数字的数?
(1)六位数且是奇数;
(2)个位上的数字不是5的六位数;
(3)不大于4 310的四位数且是偶数.
学以致用:
6.用0,1,2,…,9十个数字可组成多少个满足以下条件的没有重复数字的数?
(1)五位奇数;
(2)大于30 000的五位偶数.
学以致用:
7.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )
A.144个 B.120个 C.96个 D.72个
B
学以致用:
8.六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________
24
学以致用:
