《探究和的奇偶性》(课件)五年级下册数学人教版(共30张PPT)
文档属性
| 名称 | 《探究和的奇偶性》(课件)五年级下册数学人教版(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
因数和倍数
第6课时 探究和的奇偶性
2
1.通过探究知道两数之和的奇偶性,体会解决问题的策略。
2.借助几何直观,运用数形结合的方式,理解并掌握两数之和
的奇偶性。
在探究两数之和的奇偶性的过程中渗透解决问题的策略。
【学习目标】
【学习重点】
【学习难点】
理解两数之和的奇偶性的必然性。
创设情境 引入新课
(1)最小的质数是( )。
最小的合数是( )。
2
4
填一填。
(2)最小的偶数是( )。
最小的奇数是( )。
0
1
引入
快乐大转盘
规则:转动转盘,指针指着哪个数,就加上这个数的本身。
如果和是奇数,会得到大奖;和是偶数,则没有奖。
4
5
6
7
8
9
0
3
2
1
4
5
6
7
8
9
0
3
2
1
4
5
6
7
8
9
0
3
2
1
合作交流 探索新知
分析题意,你得到了什么信息?
例2
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
问题可以表示成下面的形式:
奇数+偶数=
偶数?
奇数?
奇数+奇数=
偶数?
奇数?
偶数+偶数=
偶数?
奇数?
小组讨论,找出解答问题的方法。
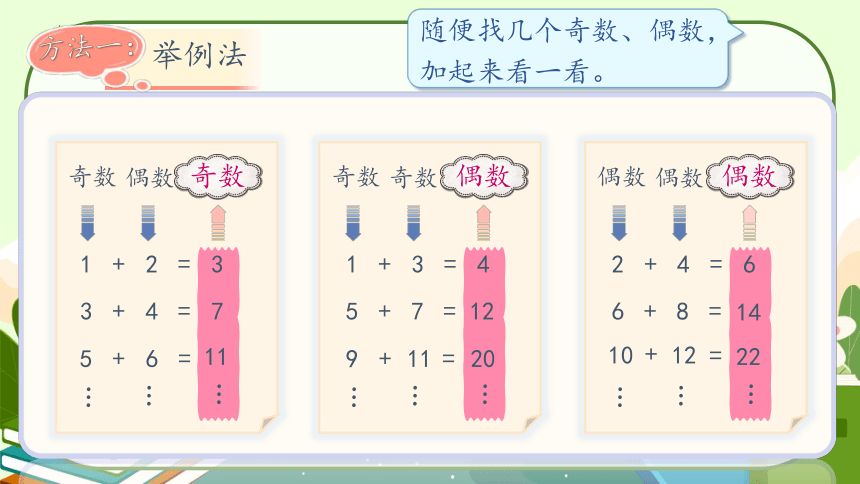
随便找几个奇数、偶数,加起来看一看。
奇数
偶数
1+2=3
3+4=7
…
…
…
5+6=
11
奇数
奇数
1+3=4
5+7=
…
…
…
9+
11
12
=
20
偶数
偶数
2+4=6
6+8=
…
…
…
22
14
10
+
12
=
方法一:
举例法
奇数
偶数
偶数
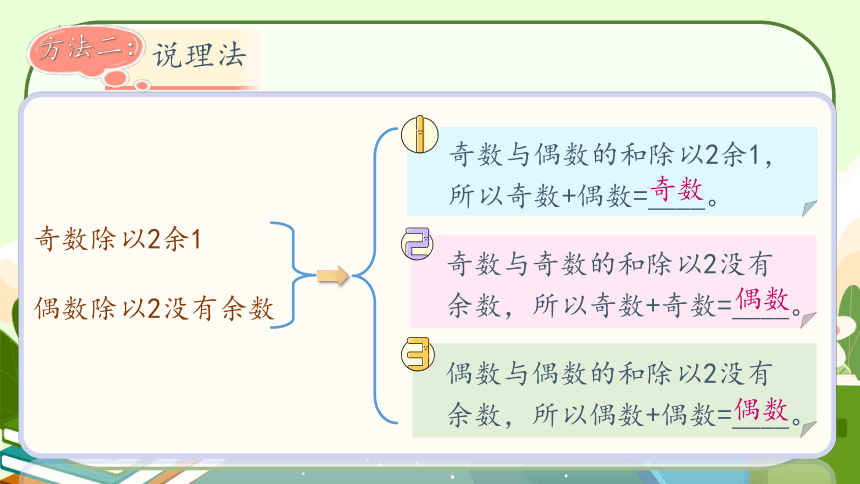
奇数除以2余1
偶数除以2没有余数
奇数与偶数的和除以2余1,
所以奇数+偶数=____。
奇数与奇数的和除以2没有余数,所以奇数+奇数=____。
偶数与偶数的和除以2没有余数,所以偶数+偶数=____。
奇数
偶数
偶数
方法二:
说理法
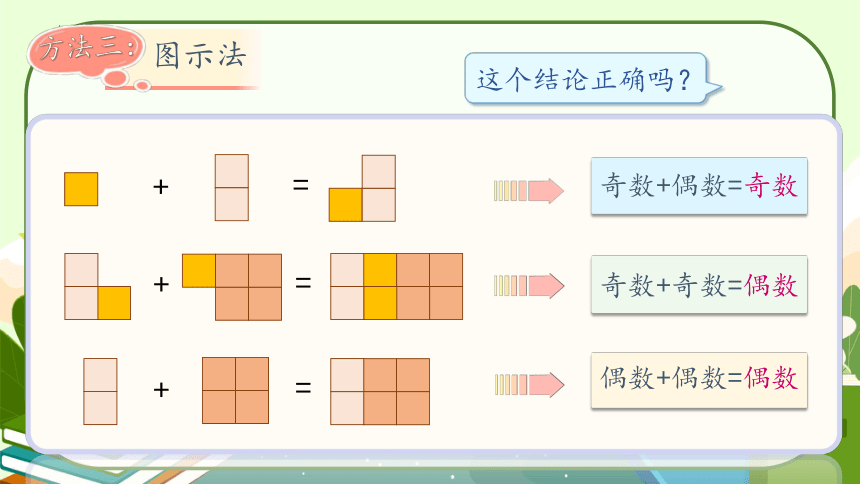
这个结论正确吗?
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
+
=
+
=
+
=
方法三:
图示法
我们可以再找些大数试一试。
319+534=853
奇数+偶数=奇数
534+852=1386
偶数+偶数=偶数
319+1045=1364
奇数+奇数=偶数
还有其他方法吗?你觉得哪种方法好?
两数之和的奇偶性:
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
小 结
应用迁移 巩固提高
3×5=15
7×9=63
……
所得的积除以2余1
奇数×奇数=奇数
2×3=6
5×6=30
……
所得的积除以2没有余数
偶数×奇数=偶数
1
奇数与奇数的积是奇数还是偶数?奇数与偶数的积是
奇数还是偶数?偶数与偶数的积呢?(教材P16第4题)
2×4=8
6×8=48
……
偶数×偶数=偶数
你是怎么推理的?
1
奇数与奇数的积是奇数还是偶数?奇数与偶数的积是
奇数还是偶数?偶数与偶数的积呢?(教材P16第4题)
所得的积除以2没有余数
偶数-奇数=奇数
偶数-偶数=偶数
答:如果甲队人数为奇数,乙队人数为奇数;
如果甲队人数为偶数,乙队人数为偶数。
30是偶数
2
30名学生要分成甲、乙两队。如果甲队人数为奇数,
乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
(教材P17第5题)
甲队
乙队
随堂练习 巩固新知
被减数(奇数) 17 11 23
减数(奇数) 5 9 15
差( )
发现:奇数-奇数=( );偶数-偶数=( );
奇数-偶数=( );偶数-奇数=( )。
12
被减数(偶数) 18 42 76
减数(偶数) 0 14 42
差( )
被减数(奇数) 21 75 59
减数(偶数) 12 54 36
差( )
被减数(偶数) 10 26 64
减数(奇数) 3 17 21
差( )
2
8
偶数
18
28
34
偶数
9
21
23
奇数
7
9
43
奇数
偶数
偶数
奇数
奇数
2
写一写,你发现了什么?
两数之差的奇偶性也可以借助两数之和的奇偶性推导出来。
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
偶数-奇数=奇数
偶数-偶数=偶数
奇数-偶数=奇数
奇数-奇数=偶数
46□+58的和
302-□5的差
5□□×12的积
一定是奇数
一定是偶数
可能是奇数,
也可能是偶数
2
连一连。
当堂练习 及时反馈
1
选择。
(1)
n是一个大于0的自然数,则2n一定是( )。
A. 奇数 B. 偶数 C. 质数
(2)
一个奇数如果( ),结果是偶数。
A. 乘5 B. 加上9 C. 减去2
(3)
1~10中,所有奇数之和是( )。
A. 奇数 B. 偶数 C. 不能确定
B
B
A
奇数+奇数=偶数
5个奇数的和是奇数
(5)278×5287 ( )
偶数
(6)74189×413 ( )
(4)3179-1946 ( )
(2)7862+3106 ( )
(1)654+799 ( )
(3)817+451 ( )
偶数
奇数
偶数
奇数
奇数
2
不计算,判断下列算式的结果是奇数还是偶数。
拓展延伸 能力提升
40个奇数+40个偶数
判断:1+2+3+4+…+80的结果是奇数还是偶数?
偶数
偶数
+ =
偶数
1
不用计算,回答问题。
(1)
51个奇数+50个偶数
判断:1+2+3+4+…+101的结果是奇数还是偶数?
奇数
偶数
+ =
奇数
1
不用计算,回答问题。
(2)
和你的同桌试一试吧。
2
两人一组,一人说出大于2的偶数,另一人找出和为此数的两个质数。(教材P17第6题)
偶数10。
3+7=10。
哥德巴赫猜想
从上面第6题的游戏中我们可以看到:4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,但要证明却非常困难,因而成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
板书设计 思维导图
探究和的奇偶性
两数之和的奇偶性:
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
因数和倍数
第6课时 探究和的奇偶性
2
1.通过探究知道两数之和的奇偶性,体会解决问题的策略。
2.借助几何直观,运用数形结合的方式,理解并掌握两数之和
的奇偶性。
在探究两数之和的奇偶性的过程中渗透解决问题的策略。
【学习目标】
【学习重点】
【学习难点】
理解两数之和的奇偶性的必然性。
创设情境 引入新课
(1)最小的质数是( )。
最小的合数是( )。
2
4
填一填。
(2)最小的偶数是( )。
最小的奇数是( )。
0
1
引入
快乐大转盘
规则:转动转盘,指针指着哪个数,就加上这个数的本身。
如果和是奇数,会得到大奖;和是偶数,则没有奖。
4
5
6
7
8
9
0
3
2
1
4
5
6
7
8
9
0
3
2
1
4
5
6
7
8
9
0
3
2
1
合作交流 探索新知
分析题意,你得到了什么信息?
例2
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
问题可以表示成下面的形式:
奇数+偶数=
偶数?
奇数?
奇数+奇数=
偶数?
奇数?
偶数+偶数=
偶数?
奇数?
小组讨论,找出解答问题的方法。
随便找几个奇数、偶数,加起来看一看。
奇数
偶数
1+2=3
3+4=7
…
…
…
5+6=
11
奇数
奇数
1+3=4
5+7=
…
…
…
9+
11
12
=
20
偶数
偶数
2+4=6
6+8=
…
…
…
22
14
10
+
12
=
方法一:
举例法
奇数
偶数
偶数
奇数除以2余1
偶数除以2没有余数
奇数与偶数的和除以2余1,
所以奇数+偶数=____。
奇数与奇数的和除以2没有余数,所以奇数+奇数=____。
偶数与偶数的和除以2没有余数,所以偶数+偶数=____。
奇数
偶数
偶数
方法二:
说理法
这个结论正确吗?
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
+
=
+
=
+
=
方法三:
图示法
我们可以再找些大数试一试。
319+534=853
奇数+偶数=奇数
534+852=1386
偶数+偶数=偶数
319+1045=1364
奇数+奇数=偶数
还有其他方法吗?你觉得哪种方法好?
两数之和的奇偶性:
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
小 结
应用迁移 巩固提高
3×5=15
7×9=63
……
所得的积除以2余1
奇数×奇数=奇数
2×3=6
5×6=30
……
所得的积除以2没有余数
偶数×奇数=偶数
1
奇数与奇数的积是奇数还是偶数?奇数与偶数的积是
奇数还是偶数?偶数与偶数的积呢?(教材P16第4题)
2×4=8
6×8=48
……
偶数×偶数=偶数
你是怎么推理的?
1
奇数与奇数的积是奇数还是偶数?奇数与偶数的积是
奇数还是偶数?偶数与偶数的积呢?(教材P16第4题)
所得的积除以2没有余数
偶数-奇数=奇数
偶数-偶数=偶数
答:如果甲队人数为奇数,乙队人数为奇数;
如果甲队人数为偶数,乙队人数为偶数。
30是偶数
2
30名学生要分成甲、乙两队。如果甲队人数为奇数,
乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
(教材P17第5题)
甲队
乙队
随堂练习 巩固新知
被减数(奇数) 17 11 23
减数(奇数) 5 9 15
差( )
发现:奇数-奇数=( );偶数-偶数=( );
奇数-偶数=( );偶数-奇数=( )。
12
被减数(偶数) 18 42 76
减数(偶数) 0 14 42
差( )
被减数(奇数) 21 75 59
减数(偶数) 12 54 36
差( )
被减数(偶数) 10 26 64
减数(奇数) 3 17 21
差( )
2
8
偶数
18
28
34
偶数
9
21
23
奇数
7
9
43
奇数
偶数
偶数
奇数
奇数
2
写一写,你发现了什么?
两数之差的奇偶性也可以借助两数之和的奇偶性推导出来。
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
偶数-奇数=奇数
偶数-偶数=偶数
奇数-偶数=奇数
奇数-奇数=偶数
46□+58的和
302-□5的差
5□□×12的积
一定是奇数
一定是偶数
可能是奇数,
也可能是偶数
2
连一连。
当堂练习 及时反馈
1
选择。
(1)
n是一个大于0的自然数,则2n一定是( )。
A. 奇数 B. 偶数 C. 质数
(2)
一个奇数如果( ),结果是偶数。
A. 乘5 B. 加上9 C. 减去2
(3)
1~10中,所有奇数之和是( )。
A. 奇数 B. 偶数 C. 不能确定
B
B
A
奇数+奇数=偶数
5个奇数的和是奇数
(5)278×5287 ( )
偶数
(6)74189×413 ( )
(4)3179-1946 ( )
(2)7862+3106 ( )
(1)654+799 ( )
(3)817+451 ( )
偶数
奇数
偶数
奇数
奇数
2
不计算,判断下列算式的结果是奇数还是偶数。
拓展延伸 能力提升
40个奇数+40个偶数
判断:1+2+3+4+…+80的结果是奇数还是偶数?
偶数
偶数
+ =
偶数
1
不用计算,回答问题。
(1)
51个奇数+50个偶数
判断:1+2+3+4+…+101的结果是奇数还是偶数?
奇数
偶数
+ =
奇数
1
不用计算,回答问题。
(2)
和你的同桌试一试吧。
2
两人一组,一人说出大于2的偶数,另一人找出和为此数的两个质数。(教材P17第6题)
偶数10。
3+7=10。
哥德巴赫猜想
从上面第6题的游戏中我们可以看到:4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,但要证明却非常困难,因而成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
板书设计 思维导图
探究和的奇偶性
两数之和的奇偶性:
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
