二元一次方程组的解法[下学期]
图片预览






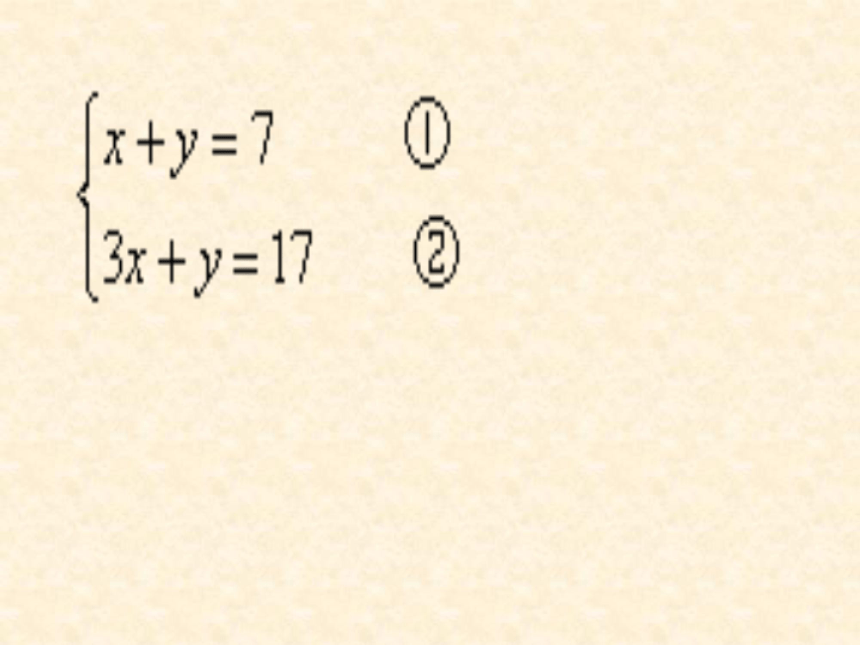


文档简介
课件21张PPT。P.26 问题2 某校现有校舍20000 ,
计划拆除部分旧校舍,改建新校舍
,使校舍总面积增加30%。若建造
新校舍的面积为被拆除的旧校舍的
面积的4倍,那么应该拆除多少旧
校舍,建造多少新校舍?解:设应该拆除旧校舍x 平方米,
则建造新校舍 4x 平方米。
根据题意列方程得:
4x - x = 20000 × 30%解:设应该拆除旧校舍x平方米,
则建造新校舍y平方米。根据题
意列方程组得:
???
分析:由方程(2)表明,y 与 4x 是两个
相等的量,因此方程(1)中的 y 可以用 4x
来代替,即得??
??????????? 4x - x = 20000 × 30%.........(3)??
我们把这个过程称为“把方程(2)代入
方程(1)”,记作“把(2)代入(1)”,
并把所得的方程记作 “方程(3)”,此时我
们可以发现方程(3)是一个一元一次方程
,从而可以求出未知数 x 的值,然后求
出y的值。解:把(2)代入(1),得
?4x - x = 20000 × 30%??? (3)
???? 3x = 6000
????? x = 2000
?把x = 2000 代入(2),得
????? y = 8000解下列方程组:分析:
?这里的两个方程中,没有一个是直接用
一个未知数表示另一个未知数的形式,
所以不能直接代入,怎么办呢?
?我们可以看到,在代入前需要做一些准
备工作,即选择一个合适的方程,把它
化成用一个未知数表示另一个未知数的
形式。
所以? 原方程组的解是 它的一般步骤是:
(1)从方程组中选一个系数较简单的方
程,将这个方程中的一个未知数用含另一
个未知数的代数式表示出来,也就是得到
方程③;
(2)将方程③代入另一个方程中,消去这
个未知数,得到一个一元一次方程;
(3)解这个一元一次方程,求出一个未知
数的值;
(4)把求得的未知数的值代入方程③,求
出另一个未知数的值,从而得到方程组的解。
(5)检验,可以心算或在草稿上演算。主要步骤: 基本思路:写解求解代入消去一个元分别求出两个未知数的值写出方程组的解变形用一个未知数的代数式
表示另一个未知数消元: 二元 一元1、解二元一次方程组的基本思路是什么?2、用代入法解方程的步骤是什么?检验检验方程组的解解下列方程组:
?*注意对照一般步骤,过程要写完整。???????????????????
?**请你想一想在解题过程中要注意些什么????????????????????????????解方程组 分析:本题可以仿照前面的解法,依次求解。
同时我们可以发现:
方程(2)的括号内是 x + y ,而方程(1)
的左边也是 x + y ,由此我们可以把(1)
直接代入(2),即得......
解:把(1)代入(2),得
?????????
解得: y = 4?
?
将 y = 4 代入(1)得
?????????? x + 4 = 9?
???????????????? x = 5?
所以? 原方程组的解是 1 、消元(为把二元 一元)2、用一个未知数的代数式表示另一个未知数
1、已知 |2x-3y-5| 和 (3x+2y-1) 的值
互为相反数,求x, y 的值?2解:由题意知:{2x=3y+5 3x=1–2y 即:{x+3y=﹣23、已知方程组{ 由于甲看错了方程①中的a,得到方程组的解为 { ,乙看错了方程②中的b,得到方程组的解为{
若按正确的a,b计算,求原方程组的解?ax–3y=5 ① 3x+by= 1 ②9﹣4b=1 b= 24a﹣3=5a=2∴原方程组为:{ 2x–3y=5 3x+2y=1 解法二:由x-2y=10得x=10+2y再代入
方程组,解出m.5、在y=kx+b中,当x=1时,y=5;
当x=4 时,y= -1.求k. b的值?
计划拆除部分旧校舍,改建新校舍
,使校舍总面积增加30%。若建造
新校舍的面积为被拆除的旧校舍的
面积的4倍,那么应该拆除多少旧
校舍,建造多少新校舍?解:设应该拆除旧校舍x 平方米,
则建造新校舍 4x 平方米。
根据题意列方程得:
4x - x = 20000 × 30%解:设应该拆除旧校舍x平方米,
则建造新校舍y平方米。根据题
意列方程组得:
???
分析:由方程(2)表明,y 与 4x 是两个
相等的量,因此方程(1)中的 y 可以用 4x
来代替,即得??
??????????? 4x - x = 20000 × 30%.........(3)??
我们把这个过程称为“把方程(2)代入
方程(1)”,记作“把(2)代入(1)”,
并把所得的方程记作 “方程(3)”,此时我
们可以发现方程(3)是一个一元一次方程
,从而可以求出未知数 x 的值,然后求
出y的值。解:把(2)代入(1),得
?4x - x = 20000 × 30%??? (3)
???? 3x = 6000
????? x = 2000
?把x = 2000 代入(2),得
????? y = 8000解下列方程组:分析:
?这里的两个方程中,没有一个是直接用
一个未知数表示另一个未知数的形式,
所以不能直接代入,怎么办呢?
?我们可以看到,在代入前需要做一些准
备工作,即选择一个合适的方程,把它
化成用一个未知数表示另一个未知数的
形式。
所以? 原方程组的解是 它的一般步骤是:
(1)从方程组中选一个系数较简单的方
程,将这个方程中的一个未知数用含另一
个未知数的代数式表示出来,也就是得到
方程③;
(2)将方程③代入另一个方程中,消去这
个未知数,得到一个一元一次方程;
(3)解这个一元一次方程,求出一个未知
数的值;
(4)把求得的未知数的值代入方程③,求
出另一个未知数的值,从而得到方程组的解。
(5)检验,可以心算或在草稿上演算。主要步骤: 基本思路:写解求解代入消去一个元分别求出两个未知数的值写出方程组的解变形用一个未知数的代数式
表示另一个未知数消元: 二元 一元1、解二元一次方程组的基本思路是什么?2、用代入法解方程的步骤是什么?检验检验方程组的解解下列方程组:
?*注意对照一般步骤,过程要写完整。???????????????????
?**请你想一想在解题过程中要注意些什么????????????????????????????解方程组 分析:本题可以仿照前面的解法,依次求解。
同时我们可以发现:
方程(2)的括号内是 x + y ,而方程(1)
的左边也是 x + y ,由此我们可以把(1)
直接代入(2),即得......
解:把(1)代入(2),得
?????????
解得: y = 4?
?
将 y = 4 代入(1)得
?????????? x + 4 = 9?
???????????????? x = 5?
所以? 原方程组的解是 1 、消元(为把二元 一元)2、用一个未知数的代数式表示另一个未知数
1、已知 |2x-3y-5| 和 (3x+2y-1) 的值
互为相反数,求x, y 的值?2解:由题意知:{2x=3y+5 3x=1–2y 即:{x+3y=﹣23、已知方程组{ 由于甲看错了方程①中的a,得到方程组的解为 { ,乙看错了方程②中的b,得到方程组的解为{
若按正确的a,b计算,求原方程组的解?ax–3y=5 ① 3x+by= 1 ②9﹣4b=1 b= 24a﹣3=5a=2∴原方程组为:{ 2x–3y=5 3x+2y=1 解法二:由x-2y=10得x=10+2y再代入
方程组,解出m.5、在y=kx+b中,当x=1时,y=5;
当x=4 时,y= -1.求k. b的值?
