【模块七 图形的变换】专题1 尺规作图、视图与投影-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块七 图形的变换】专题1 尺规作图、视图与投影-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 20:30:19 | ||
图片预览


文档简介
2023年中考数学第一轮复习
模块七 图形的变换
专题1 尺规作图、视图与投影
尺 规 作 图 作一条线段等于已知线段 ①作射线AB; ②在射线AB上截取AC=a,则线段AC就是所求作的线段.
作一个角等于已知角 ①作射线O′A′; ②以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D; ③以O′为圆心,以OC的长为半径画弧,交O′A′于点C′;④以C′为圆心,以CD的长为半径画弧,交前弧于点D′; ⑤过点O′,D′作射线O′B′,则∠A′O′B′就是所求作的角.
作已知角的平分线 ①在OA,OB上分别截取OD,OE,使OD=OE; ②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C; ③作射线OC,则OC就是∠AOB的平分线.
作线段的垂直平分线 ①分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于点C,D; ②作直线CD,则直线CD就是线段AB的垂直平分线.
过定点作已知直线的垂线 不论点是否在已知直线上,都可以利用线段垂直平分线的作法作出.
2.平行投影与中心投影
(1)平行投影:由平行光线形成的投影叫做平行投影.太阳光线可以看成是平行光线.
同一时刻,所有物体在阳光下的影长与其实际长度成比例:=.
(2)中心投影:由同一点(点光源)发出的光线形成的投影.例如:路灯.
3.三视图
(1)三视图的画法:主视图和俯视图的长相等;主视图和左视图的高相等;左视图和俯视图的宽相等.看得见的部分画成实线;看不见的部分画成虚线.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
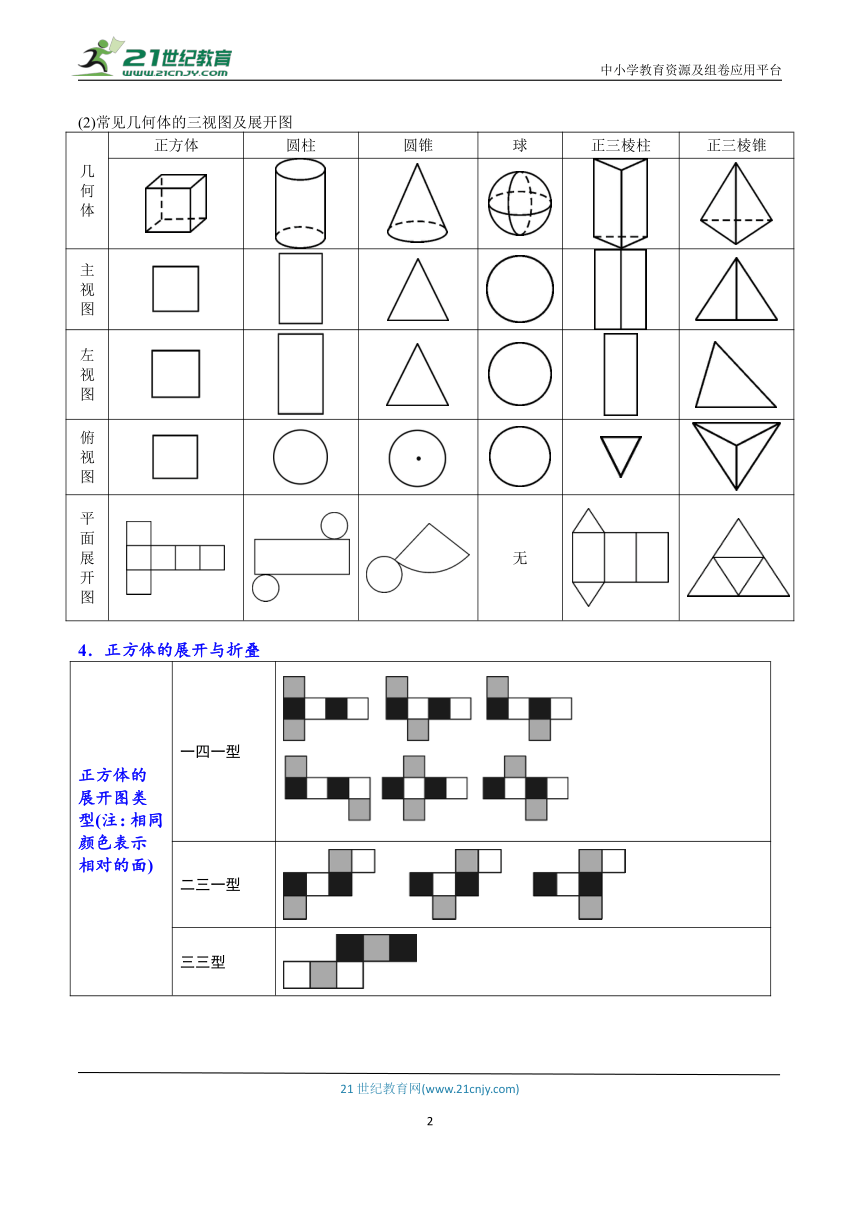
(2)常见几何体的三视图及展开图
几何 体 正方体 圆柱 圆锥 球 正三棱柱 正三棱锥
主视 图
左视 图
俯视 图
平面展 开图 无
4.正方体的展开与折叠
正方体的展开图类型(注:相同颜色表示相对的面) 一四一型
二三一型
三三型
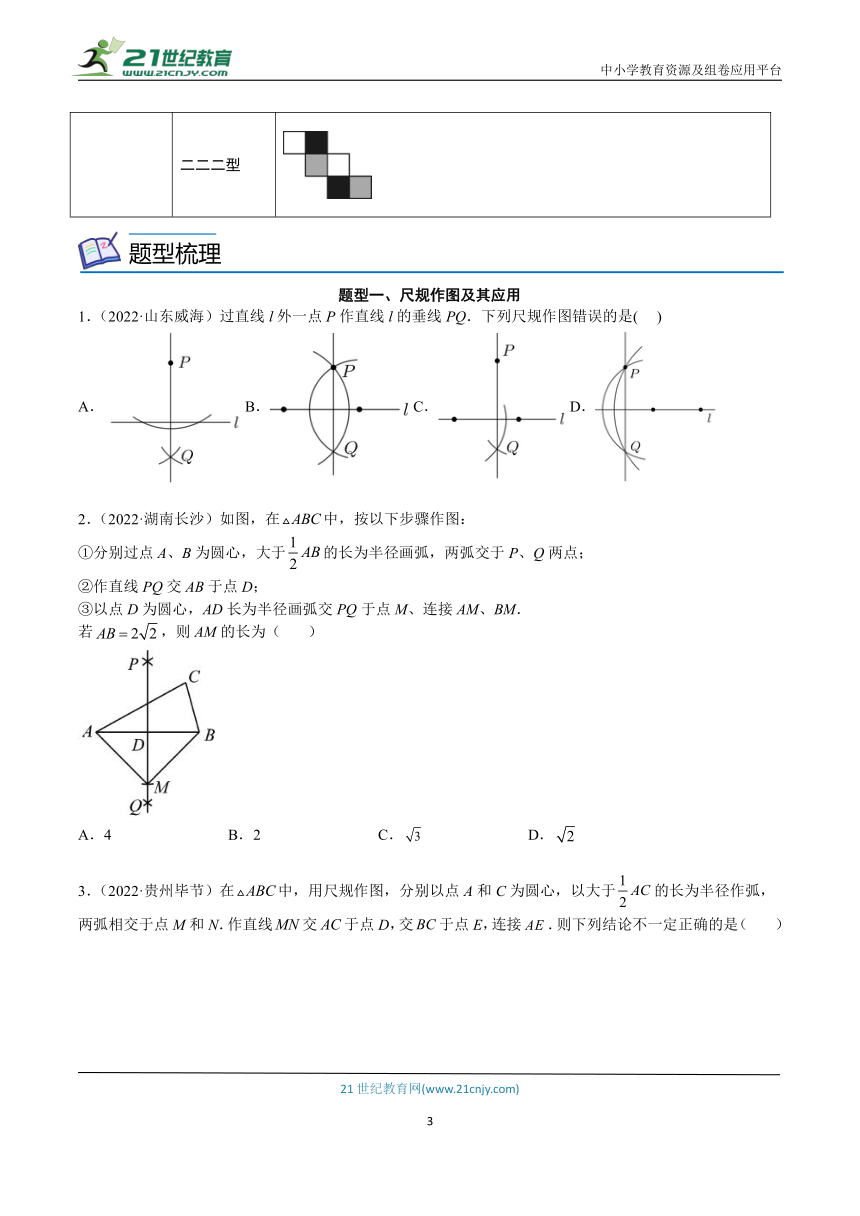
二二二型
题型一、尺规作图及其应用
1.(2022·山东威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.C.D.
2.(2022·湖南长沙)如图,在中,按以下步骤作图:
①分别过点A、B为圆心,大于的长为半径画弧,两弧交于P、Q两点;
②作直线PQ交AB于点D;
③以点D为圆心,AD长为半径画弧交PQ于点M、连接AM、BM.
若,则AM的长为( )
A.4 B.2 C. D.
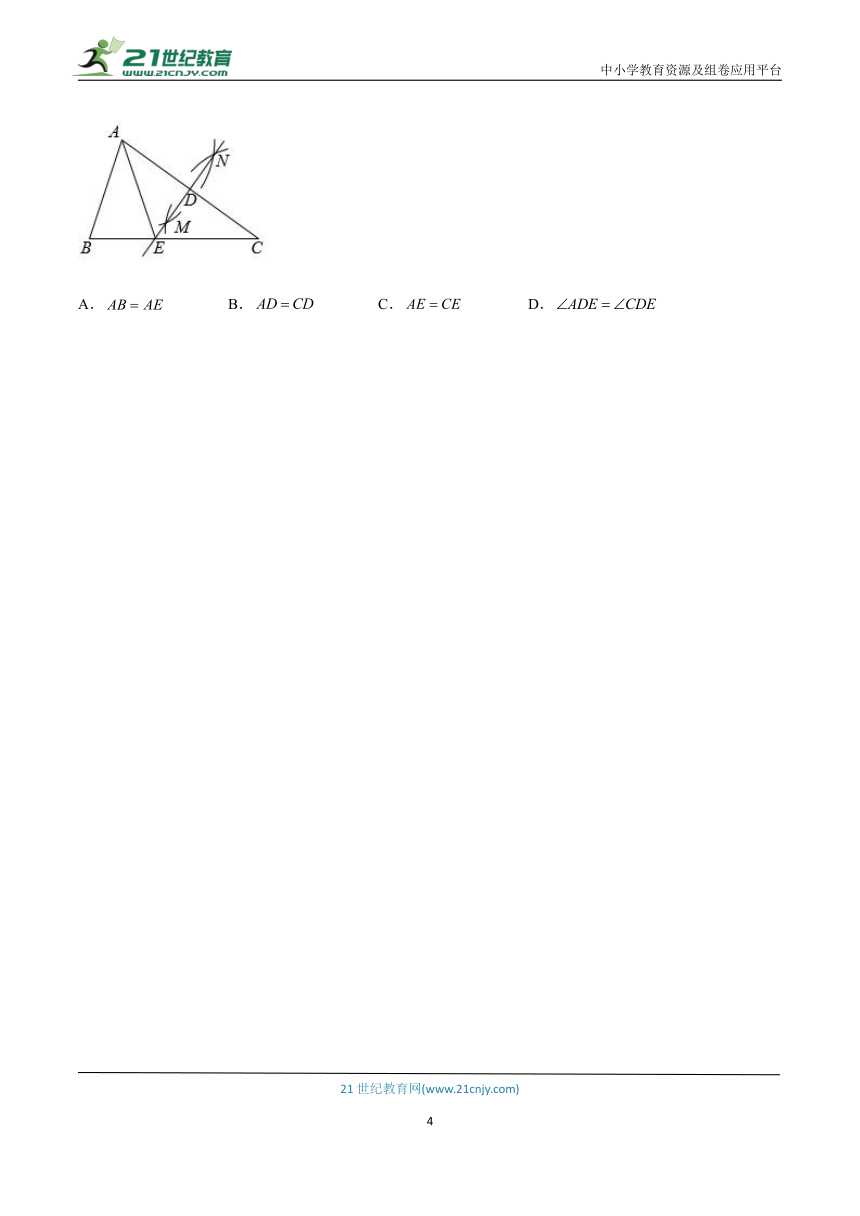
3.(2022·贵州毕节)在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )
A. B. C. D.
4.(2022·陕西·中考真题)如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
5.(2022·广西)如图,在中,BD是它的一条对角线,
(1)求证:;
(2)尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);
(3)连接BE,若,求的度数.
6.(2022·江苏无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,,则四边形ABCD的面积为 .(如需画草图,请使用试卷中的图2)
7.(2022·黑龙江绥化)已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
8.(2022·内蒙古赤峰)如图,已知中,,,.
(1)作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的周长.
题型二、几何体的三视图
1.(2022·山东临沂)如图所示的三棱柱的展开图不可能是( )
A. B. C. D.
2.(2022·湖南邵阳)下列四个图形中,圆柱体的俯视图是( )
A. B. C. D.
3.(2022·内蒙古赤峰)下面几何体的俯视图是( )
A. B. C. D.
4.(2022·辽宁营口)如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B. C. D.
5.(2022·四川泸州)如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )
A. B. C. D.
6.(2022·广西河池)下列几何体中,三视图的三个视图完全相同的几何体是( )
A. B. C. D.
7.(2022·黑龙江)如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
8.(2022 包头)几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4
C.6 D.9
9.(2022·浙江金华·中考真题)如图,圆柱的底面直径为,高为,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
题型三、正方体的展开与折叠
1.(2022·四川内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
2.(2022·湖北恩施)下图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是( )
A.“恩” B.“乡” C.“村” D.“兴”
3.(2022·黑龙江绥化·中考真题)下列图形中,正方体展开图错误的是( )
A.B.C. D.
题型四、投影
1.(2022 靖西模拟)如图,小莉用灯泡O照射一个矩形硬纸片ABCD,在墙上形成矩形影子A′B′C′D′,现测得OA=2 cm,OA′=5 cm,纸片ABCD的面积为8 cm2,则影子A′B′C′D′的面积为 cm2.
2.(2022·广西)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是________米.
3.(2022·浙江温州·中考真题)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于___________米.转动时,叶片外端离地面的最大高度等于___________米.
4.(2022·陕西·中考真题)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
2023年中考数学第一轮复习
模块七 图形的变换
专题1 尺规作图、视图与投影
尺 规 作 图 作一条线段等于已知线段 ①作射线AB; ②在射线AB上截取AC=a,则线段AC就是所求作的线段.
作一个角等于已知角 ①作射线O′A′; ②以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D; ③以O′为圆心,以OC的长为半径画弧,交O′A′于点C′;④以C′为圆心,以CD的长为半径画弧,交前弧于点D′; ⑤过点O′,D′作射线O′B′,则∠A′O′B′就是所求作的角.
作已知角的平分线 ①在OA,OB上分别截取OD,OE,使OD=OE; ②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C; ③作射线OC,则OC就是∠AOB的平分线.
作线段的垂直平分线 ①分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于点C,D; ②作直线CD,则直线CD就是线段AB的垂直平分线.
过定点作已知直线的垂线 不论点是否在已知直线上,都可以利用线段垂直平分线的作法作出.
2.平行投影与中心投影
(1)平行投影:由平行光线形成的投影叫做平行投影.太阳光线可以看成是平行光线.
同一时刻,所有物体在阳光下的影长与其实际长度成比例:=.
(2)中心投影:由同一点(点光源)发出的光线形成的投影.例如:路灯.
3.三视图
(1)三视图的画法:主视图和俯视图的长相等;主视图和左视图的高相等;左视图和俯视图的宽相等.看得见的部分画成实线;看不见的部分画成虚线.
(2)常见几何体的三视图及展开图
几何 体 正方体 圆柱 圆锥 球 正三棱柱 正三棱锥
主视 图
左视 图
俯视 图
平面展 开图 无
4.正方体的展开与折叠
正方体的展开图类型(注:相同颜色表示相对的面) 一四一型
二三一型
三三型
二二二型
题型一、尺规作图及其应用
1.(2022·山东威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.C.D.
【答案】C
【分析】根据线段垂直平分线的逆定理及两点确定一条直线一一判断即可.
【详解】A、如图,连接AP、AQ、BP、BQ,
AP=BP,AQ=BQ,
点P在线段AB的垂直平分线上,点Q在线段AB的垂直平分线上,
直线PQ垂直平分线线段AB,即直线l垂直平分线线段PQ,本选项不符合题意;
B、如图,连接AP、AQ、BP、BQ,
AP= AQ,BP =BQ,点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,
直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,本选项不符合题意;
C、C项无法判定直线PQ垂直直线l,本选项符合题意;
D、如图,连接AP、AQ、BP、BQ,
AP= AQ,BP =BQ,
点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,
直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,
本选项不符合题意;故选:C.
2.(2022·湖南长沙)如图,在中,按以下步骤作图:
①分别过点A、B为圆心,大于的长为半径画弧,两弧交于P、Q两点;
②作直线PQ交AB于点D;
③以点D为圆心,AD长为半径画弧交PQ于点M、连接AM、BM.
若,则AM的长为( )
A.4 B.2 C. D.
【答案】B
【分析】根据作图可知垂直平分,,是等腰直角三角形,据此即可求解.
【详解】解:由作图可得垂直平分,
则是等腰直角三角形
∴由勾股定理得:故选:B.
【点睛】本题考查了作垂线,等腰直角三角形的性质,勾股定理,掌握基本作图理解题意是解题的关键.
3.(2022·贵州毕节)在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )
A. B. C. D.
【答案】A
【分析】根据作图可知AM=CM,AN=CN,所以MN是AC的垂直平分线,根据垂直平分线的性质,线段垂直平分线上的点到线段两端的距离相等,且平分此点到线段两端构成的夹角,分别对各选项进行判断.
【详解】由题意得,MN垂直平分线段AC,
∴,,
所以B、C、D正确,
因为点B的位置不确定,
所以不能确定AB=AE,故选 A
【点睛】本题考查了线段垂直平分线,熟练掌握线段垂直平分线的作图方法和性质是解题的关键.
4.(2022·陕西·中考真题)如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
【答案】见解析
【分析】作的角平分线即可.
【详解】解:如图,射线即为所求作.
【点睛】本题考查了角平分线、三角形外角的性质、平行线的判定,解题的关键是掌握平行线的判定定理.
5.(2022·广西)如图,在中,BD是它的一条对角线,
(1)求证:;
(2)尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);
(3)连接BE,若,求的度数.
【答案】(1)见解析
(2)见解析
(3)50°
【分析】(1)由平行四边形的性质得出,可利用“SSS”证明三角形全等;
(2)根据垂直平分线的作法即可解答;
(3)根据垂直平分线的性质可得,由等腰三角形的性质可得,再根据三角形外角的性质求解即可.
(1)
四边形ABCD是平行四边形,
,
,
(2)
如图,EF即为所求;
(3)
BD的垂直平分线为EF,
,
,
,
,
.
【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,垂直平分线的作法和性质,等腰三角形的性质及三角形外角的性质,熟练掌握知识点是解题的关键.
6.(2022·江苏无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,,则四边形ABCD的面积为 .(如需画草图,请使用试卷中的图2)
【答案】(1)见解析
(2)
【分析】(1)先作∠DAC=∠ACB,再利用垂直平分线的性质作,即可找出点D;
(2)由题意可知四边形ABCD是梯形,利用直角三角形的性质求出AE、BE、CE、AD的长,求出梯形的面积即可.
(1)
解:如图,
∴点D为所求点.
(2)
解:过点A作AE垂直于BC,垂足为E,
∵,,
∴,
∵,
∴,,
∴,
∵∠DAC=∠ACB,
∴,四边形ABCD是梯形,
∴,
∴四边形AECD是矩形,
∴,
∴四边形ABCD的面积为,
故答案为:.
【点睛】本题考查作图,作相等的角,根据垂直平分线的性质做垂线,根据直角三角形的性质及勾股定理求线段的长,正确作出图形是解答本题的关键.
7.(2022·黑龙江绥化)已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
【答案】(1)作图见详解
(2)9.1
【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;
(2)利用割补法,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,这样将△ABC分成三个小三角形,这三个小三角形分别以△ABC的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.
(1)
解:如下图所示,O为所求作点,
(2)
解:如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,
∵内切圆的半径为1.3,
∴OD=OF=OE=1.3,
∵三角形ABC的周长为14,
∴AB+BC+AC=14,
则
故三角形ABC的面积为9.1.
【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.
8.(2022·内蒙古赤峰)如图,已知中,,,.
(1)作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的周长.
【答案】(1)见解析
(2)
【分析】(1)利用基本作图,作BC的垂直平分线分别交、于点、;
(2)根据平行线分线段成比例计算即可.
(1)
如图所示,点D、H即为所求
(2)
在(1)的条件下,,
∵,
∴DH∥AC,
∴
∴,解得
∴
故答案为:.
【点睛】本题考查尺规作图中的作垂直平分线、平行线分段成比例、垂直平分线的性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
题型二、几何体的三视图
1.(2022·山东临沂)如图所示的三棱柱的展开图不可能是( )
A. B. C. D.
【答案】D
【分析】三棱柱的表面展开图的特点,由三个长方形的侧面和上下两个三角形的底面组成.从而可得答案.
【详解】解:选项A、B、C均可能是该三棱柱展开图,不符合题意,
而选项D中的两个底面会重叠,不可能是它的表面展开图,符合题意,
故选:D.
2.(2022·湖南邵阳)下列四个图形中,圆柱体的俯视图是( )
A. B. C. D.
【答案】D
【分析】根据俯视图是从上面看到的视图进而得出答案即可.
【详解】解:竖直放置的圆柱体,从上面看是圆,
所以俯视图是圆.
故选∶D.
3.(2022·内蒙古赤峰)下面几何体的俯视图是( )
A. B. C. D.
【答案】B
【分析】俯视图是从物体的上面看得到的视图.
【详解】圆台的俯视图是一个同心圆环.
故选:B.
【点睛】本题考查几何体的三视图,主要考查学生空间想象能力及对立体图形的认知能力.
4.(2022·辽宁营口)如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B. C. D.
【答案】B
【分析】左视图是从物体的左边观察得到的图形,结合选项进行判断即可.
【详解】解:从左边看,有两列,从左到右第一列是两个正方形,第二列底层是一个正方形.
故选:B.
【点睛】本题考查了简单组合体的三视图,属于基础题,解答本题的关键是掌握左视图的定义.
5.(2022·四川泸州)如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )
A. B. C. D.
【答案】C
【分析】观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形即可判定.
【详解】解:由俯视图的定义可知:从上往下观察发现∶
故选C.
【点睛】本题考查三视图,解题的关键是熟练掌握俯视图是从物体上面看所得到的图形.
6.(2022·广西河池)下列几何体中,三视图的三个视图完全相同的几何体是( )
A. B. C. D.
【答案】D
【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可.
【详解】解:A.三棱柱的俯视图与主视图和左视图都不同,故此选项错误;
B.圆柱的俯视图与主视图和左视图不同,故此选项错误;
C.圆锥的俯视图与主视图和左视图不同,故此选项错误;
D.球的三视图完全相同,都是圆,故此选项正确.故选:D.
【点睛】本题主要考查了三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.
7.(2022·黑龙江)如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
【答案】B
【分析】这个几何体共有2层,由俯视图可得第一层小正方体的个数,由左视图可得第二层小正方体的最多个数,再相加即可.
【详解】由俯视图可知最底层有5个小正方体,由左视图可知这个几何体有两层,其中第二层最多有3个,那么搭成这个几何体所需小正方体最多有个.
故选:B.
【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
8.(2022 包头)几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4
C.6 D.9
【答案】B
【分析】根据该几何体的俯视图以及该位置小正方体的个数,可以画出左视图,从而求出左视图的面积;
【详解】由俯视图以及该位置小正方体的个数,左视图共有两列,第一列两个小正方体,第二列两个小正方体,可以画出左视图如图,所以这个几何体的左视图的面积为4故选:B
【点睛】本题考查了物体的三视图,解题饿到关键是根据俯视图,以及该位置小正方体的个数,正确作出左视图.
9.(2022·浙江金华·中考真题)如图,圆柱的底面直径为,高为,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
【答案】C
【分析】根据圆柱的侧面展开特征,两点之间线段最短判断即可;
【详解】解:∵AB为底面直径,
∴将圆柱侧面沿“剪开”后, B点在长方形上面那条边的中间,
∵两点之间线段最短,故选: C.
【点睛】本题考查了圆柱的侧面展开,掌握两点之间线段最短是解题关键.
题型三、正方体的展开与折叠
1.(2022·四川内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
【答案】C
【分析】根据正方体表面展开图的特征进行判断即可.
【详解】解:由正方体表面展开图的“相间、Z端是对面”可知,
“话”与“走”是对面,
故答案为:C.
【点睛】本题考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的前提.
2.(2022·湖北恩施)下图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是( )
A.“恩” B.“乡” C.“村” D.“兴”
【答案】D
【分析】根据正方体的平面展开图的特点即可得.
【详解】解:由正方体的平面展开图的特点得:“恩”字与“乡”字在相对面上,“施”字与“村”字在相对面上,“振”字与“兴”字在相对面上,
故选:D.
3.(2022·黑龙江绥化·中考真题)下列图形中,正方体展开图错误的是( )
A.B.C. D.
【答案】D
【分析】利用正方体及其表面展开图的特点解题.
【详解】D选项出现了“田字形”,折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,A、B、C选项是一个正方体的表面展开图.故选:D.
题型四、投影
1.(2022 靖西模拟)如图,小莉用灯泡O照射一个矩形硬纸片ABCD,在墙上形成矩形影子A′B′C′D′,现测得OA=2 cm,OA′=5 cm,纸片ABCD的面积为8 cm2,则影子A′B′C′D′的面积为 cm2.
【答案】50
2.(2022·广西)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是________米.
【答案】134
【分析】在同一时刻物高和影子成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,根据相似三角形的性质即可得.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:134.
【点睛】本题考查了相似三角形的应用,解题的关键是了解:同一时刻物高和影长成正比.
3.(2022·浙江温州·中考真题)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于___________米.转动时,叶片外端离地面的最大高度等于___________米.
【答案】 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,由题意可知,点O是AB的中点,
∵,∴点H是CD的中点,
∵,∴,
∴,
又∵由题意可知:,∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,∴,
∵由题意可知:,
又∵,∴,
∴,∴,∴,,
∵,∴四边形IHDJ是平行四边形,∴,
∵,∴,,,
∵在中,由勾股定理得:,
∴,∴,
∴,
∴叶片外端离地面的最大高度等于,故答案为:10,.
【点睛】本题主要考查了投影和相似的应用,及勾股定理和平行四边形的判定与性质,正确作出辅助线是解答本题的关键.
4.(2022·陕西·中考真题)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
【答案】旗杆的高AB为3米.
【分析】证明△AOD∽△EFG,利用相似比计算出AO的长,再证明△BOC∽△AOD,然后利用相似比计算OB的长,进一步计算即可求解.
【详解】解:∵AD∥EG,∴∠ADO=∠EGF.
又∵∠AOD=∠EFG=90°,∴△AOD∽△EFG.
∴.∴.
同理,△BOC∽△AOD.∴.∴.
∴AB=OA OB=3(米).∴旗杆的高AB为3米.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.
模块七 图形的变换
专题1 尺规作图、视图与投影
尺 规 作 图 作一条线段等于已知线段 ①作射线AB; ②在射线AB上截取AC=a,则线段AC就是所求作的线段.
作一个角等于已知角 ①作射线O′A′; ②以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D; ③以O′为圆心,以OC的长为半径画弧,交O′A′于点C′;④以C′为圆心,以CD的长为半径画弧,交前弧于点D′; ⑤过点O′,D′作射线O′B′,则∠A′O′B′就是所求作的角.
作已知角的平分线 ①在OA,OB上分别截取OD,OE,使OD=OE; ②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C; ③作射线OC,则OC就是∠AOB的平分线.
作线段的垂直平分线 ①分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于点C,D; ②作直线CD,则直线CD就是线段AB的垂直平分线.
过定点作已知直线的垂线 不论点是否在已知直线上,都可以利用线段垂直平分线的作法作出.
2.平行投影与中心投影
(1)平行投影:由平行光线形成的投影叫做平行投影.太阳光线可以看成是平行光线.
同一时刻,所有物体在阳光下的影长与其实际长度成比例:=.
(2)中心投影:由同一点(点光源)发出的光线形成的投影.例如:路灯.
3.三视图
(1)三视图的画法:主视图和俯视图的长相等;主视图和左视图的高相等;左视图和俯视图的宽相等.看得见的部分画成实线;看不见的部分画成虚线.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
(2)常见几何体的三视图及展开图
几何 体 正方体 圆柱 圆锥 球 正三棱柱 正三棱锥
主视 图
左视 图
俯视 图
平面展 开图 无
4.正方体的展开与折叠
正方体的展开图类型(注:相同颜色表示相对的面) 一四一型
二三一型
三三型
二二二型
题型一、尺规作图及其应用
1.(2022·山东威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.C.D.
2.(2022·湖南长沙)如图,在中,按以下步骤作图:
①分别过点A、B为圆心,大于的长为半径画弧,两弧交于P、Q两点;
②作直线PQ交AB于点D;
③以点D为圆心,AD长为半径画弧交PQ于点M、连接AM、BM.
若,则AM的长为( )
A.4 B.2 C. D.
3.(2022·贵州毕节)在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )
A. B. C. D.
4.(2022·陕西·中考真题)如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
5.(2022·广西)如图,在中,BD是它的一条对角线,
(1)求证:;
(2)尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);
(3)连接BE,若,求的度数.
6.(2022·江苏无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,,则四边形ABCD的面积为 .(如需画草图,请使用试卷中的图2)
7.(2022·黑龙江绥化)已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
8.(2022·内蒙古赤峰)如图,已知中,,,.
(1)作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的周长.
题型二、几何体的三视图
1.(2022·山东临沂)如图所示的三棱柱的展开图不可能是( )
A. B. C. D.
2.(2022·湖南邵阳)下列四个图形中,圆柱体的俯视图是( )
A. B. C. D.
3.(2022·内蒙古赤峰)下面几何体的俯视图是( )
A. B. C. D.
4.(2022·辽宁营口)如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B. C. D.
5.(2022·四川泸州)如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )
A. B. C. D.
6.(2022·广西河池)下列几何体中,三视图的三个视图完全相同的几何体是( )
A. B. C. D.
7.(2022·黑龙江)如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
8.(2022 包头)几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4
C.6 D.9
9.(2022·浙江金华·中考真题)如图,圆柱的底面直径为,高为,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
题型三、正方体的展开与折叠
1.(2022·四川内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
2.(2022·湖北恩施)下图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是( )
A.“恩” B.“乡” C.“村” D.“兴”
3.(2022·黑龙江绥化·中考真题)下列图形中,正方体展开图错误的是( )
A.B.C. D.
题型四、投影
1.(2022 靖西模拟)如图,小莉用灯泡O照射一个矩形硬纸片ABCD,在墙上形成矩形影子A′B′C′D′,现测得OA=2 cm,OA′=5 cm,纸片ABCD的面积为8 cm2,则影子A′B′C′D′的面积为 cm2.
2.(2022·广西)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是________米.
3.(2022·浙江温州·中考真题)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于___________米.转动时,叶片外端离地面的最大高度等于___________米.
4.(2022·陕西·中考真题)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
2023年中考数学第一轮复习
模块七 图形的变换
专题1 尺规作图、视图与投影
尺 规 作 图 作一条线段等于已知线段 ①作射线AB; ②在射线AB上截取AC=a,则线段AC就是所求作的线段.
作一个角等于已知角 ①作射线O′A′; ②以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D; ③以O′为圆心,以OC的长为半径画弧,交O′A′于点C′;④以C′为圆心,以CD的长为半径画弧,交前弧于点D′; ⑤过点O′,D′作射线O′B′,则∠A′O′B′就是所求作的角.
作已知角的平分线 ①在OA,OB上分别截取OD,OE,使OD=OE; ②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C; ③作射线OC,则OC就是∠AOB的平分线.
作线段的垂直平分线 ①分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于点C,D; ②作直线CD,则直线CD就是线段AB的垂直平分线.
过定点作已知直线的垂线 不论点是否在已知直线上,都可以利用线段垂直平分线的作法作出.
2.平行投影与中心投影
(1)平行投影:由平行光线形成的投影叫做平行投影.太阳光线可以看成是平行光线.
同一时刻,所有物体在阳光下的影长与其实际长度成比例:=.
(2)中心投影:由同一点(点光源)发出的光线形成的投影.例如:路灯.
3.三视图
(1)三视图的画法:主视图和俯视图的长相等;主视图和左视图的高相等;左视图和俯视图的宽相等.看得见的部分画成实线;看不见的部分画成虚线.
(2)常见几何体的三视图及展开图
几何 体 正方体 圆柱 圆锥 球 正三棱柱 正三棱锥
主视 图
左视 图
俯视 图
平面展 开图 无
4.正方体的展开与折叠
正方体的展开图类型(注:相同颜色表示相对的面) 一四一型
二三一型
三三型
二二二型
题型一、尺规作图及其应用
1.(2022·山东威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )
A.B.C.D.
【答案】C
【分析】根据线段垂直平分线的逆定理及两点确定一条直线一一判断即可.
【详解】A、如图,连接AP、AQ、BP、BQ,
AP=BP,AQ=BQ,
点P在线段AB的垂直平分线上,点Q在线段AB的垂直平分线上,
直线PQ垂直平分线线段AB,即直线l垂直平分线线段PQ,本选项不符合题意;
B、如图,连接AP、AQ、BP、BQ,
AP= AQ,BP =BQ,点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,
直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,本选项不符合题意;
C、C项无法判定直线PQ垂直直线l,本选项符合题意;
D、如图,连接AP、AQ、BP、BQ,
AP= AQ,BP =BQ,
点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,
直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,
本选项不符合题意;故选:C.
2.(2022·湖南长沙)如图,在中,按以下步骤作图:
①分别过点A、B为圆心,大于的长为半径画弧,两弧交于P、Q两点;
②作直线PQ交AB于点D;
③以点D为圆心,AD长为半径画弧交PQ于点M、连接AM、BM.
若,则AM的长为( )
A.4 B.2 C. D.
【答案】B
【分析】根据作图可知垂直平分,,是等腰直角三角形,据此即可求解.
【详解】解:由作图可得垂直平分,
则是等腰直角三角形
∴由勾股定理得:故选:B.
【点睛】本题考查了作垂线,等腰直角三角形的性质,勾股定理,掌握基本作图理解题意是解题的关键.
3.(2022·贵州毕节)在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )
A. B. C. D.
【答案】A
【分析】根据作图可知AM=CM,AN=CN,所以MN是AC的垂直平分线,根据垂直平分线的性质,线段垂直平分线上的点到线段两端的距离相等,且平分此点到线段两端构成的夹角,分别对各选项进行判断.
【详解】由题意得,MN垂直平分线段AC,
∴,,
所以B、C、D正确,
因为点B的位置不确定,
所以不能确定AB=AE,故选 A
【点睛】本题考查了线段垂直平分线,熟练掌握线段垂直平分线的作图方法和性质是解题的关键.
4.(2022·陕西·中考真题)如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
【答案】见解析
【分析】作的角平分线即可.
【详解】解:如图,射线即为所求作.
【点睛】本题考查了角平分线、三角形外角的性质、平行线的判定,解题的关键是掌握平行线的判定定理.
5.(2022·广西)如图,在中,BD是它的一条对角线,
(1)求证:;
(2)尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);
(3)连接BE,若,求的度数.
【答案】(1)见解析
(2)见解析
(3)50°
【分析】(1)由平行四边形的性质得出,可利用“SSS”证明三角形全等;
(2)根据垂直平分线的作法即可解答;
(3)根据垂直平分线的性质可得,由等腰三角形的性质可得,再根据三角形外角的性质求解即可.
(1)
四边形ABCD是平行四边形,
,
,
(2)
如图,EF即为所求;
(3)
BD的垂直平分线为EF,
,
,
,
,
.
【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,垂直平分线的作法和性质,等腰三角形的性质及三角形外角的性质,熟练掌握知识点是解题的关键.
6.(2022·江苏无锡)如图,△ABC为锐角三角形.
(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,,,则四边形ABCD的面积为 .(如需画草图,请使用试卷中的图2)
【答案】(1)见解析
(2)
【分析】(1)先作∠DAC=∠ACB,再利用垂直平分线的性质作,即可找出点D;
(2)由题意可知四边形ABCD是梯形,利用直角三角形的性质求出AE、BE、CE、AD的长,求出梯形的面积即可.
(1)
解:如图,
∴点D为所求点.
(2)
解:过点A作AE垂直于BC,垂足为E,
∵,,
∴,
∵,
∴,,
∴,
∵∠DAC=∠ACB,
∴,四边形ABCD是梯形,
∴,
∴四边形AECD是矩形,
∴,
∴四边形ABCD的面积为,
故答案为:.
【点睛】本题考查作图,作相等的角,根据垂直平分线的性质做垂线,根据直角三角形的性质及勾股定理求线段的长,正确作出图形是解答本题的关键.
7.(2022·黑龙江绥化)已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
【答案】(1)作图见详解
(2)9.1
【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;
(2)利用割补法,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,这样将△ABC分成三个小三角形,这三个小三角形分别以△ABC的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.
(1)
解:如下图所示,O为所求作点,
(2)
解:如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,
∵内切圆的半径为1.3,
∴OD=OF=OE=1.3,
∵三角形ABC的周长为14,
∴AB+BC+AC=14,
则
故三角形ABC的面积为9.1.
【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.
8.(2022·内蒙古赤峰)如图,已知中,,,.
(1)作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的周长.
【答案】(1)见解析
(2)
【分析】(1)利用基本作图,作BC的垂直平分线分别交、于点、;
(2)根据平行线分线段成比例计算即可.
(1)
如图所示,点D、H即为所求
(2)
在(1)的条件下,,
∵,
∴DH∥AC,
∴
∴,解得
∴
故答案为:.
【点睛】本题考查尺规作图中的作垂直平分线、平行线分段成比例、垂直平分线的性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
题型二、几何体的三视图
1.(2022·山东临沂)如图所示的三棱柱的展开图不可能是( )
A. B. C. D.
【答案】D
【分析】三棱柱的表面展开图的特点,由三个长方形的侧面和上下两个三角形的底面组成.从而可得答案.
【详解】解:选项A、B、C均可能是该三棱柱展开图,不符合题意,
而选项D中的两个底面会重叠,不可能是它的表面展开图,符合题意,
故选:D.
2.(2022·湖南邵阳)下列四个图形中,圆柱体的俯视图是( )
A. B. C. D.
【答案】D
【分析】根据俯视图是从上面看到的视图进而得出答案即可.
【详解】解:竖直放置的圆柱体,从上面看是圆,
所以俯视图是圆.
故选∶D.
3.(2022·内蒙古赤峰)下面几何体的俯视图是( )
A. B. C. D.
【答案】B
【分析】俯视图是从物体的上面看得到的视图.
【详解】圆台的俯视图是一个同心圆环.
故选:B.
【点睛】本题考查几何体的三视图,主要考查学生空间想象能力及对立体图形的认知能力.
4.(2022·辽宁营口)如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B. C. D.
【答案】B
【分析】左视图是从物体的左边观察得到的图形,结合选项进行判断即可.
【详解】解:从左边看,有两列,从左到右第一列是两个正方形,第二列底层是一个正方形.
故选:B.
【点睛】本题考查了简单组合体的三视图,属于基础题,解答本题的关键是掌握左视图的定义.
5.(2022·四川泸州)如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )
A. B. C. D.
【答案】C
【分析】观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形即可判定.
【详解】解:由俯视图的定义可知:从上往下观察发现∶
故选C.
【点睛】本题考查三视图,解题的关键是熟练掌握俯视图是从物体上面看所得到的图形.
6.(2022·广西河池)下列几何体中,三视图的三个视图完全相同的几何体是( )
A. B. C. D.
【答案】D
【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可.
【详解】解:A.三棱柱的俯视图与主视图和左视图都不同,故此选项错误;
B.圆柱的俯视图与主视图和左视图不同,故此选项错误;
C.圆锥的俯视图与主视图和左视图不同,故此选项错误;
D.球的三视图完全相同,都是圆,故此选项正确.故选:D.
【点睛】本题主要考查了三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.
7.(2022·黑龙江)如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
【答案】B
【分析】这个几何体共有2层,由俯视图可得第一层小正方体的个数,由左视图可得第二层小正方体的最多个数,再相加即可.
【详解】由俯视图可知最底层有5个小正方体,由左视图可知这个几何体有两层,其中第二层最多有3个,那么搭成这个几何体所需小正方体最多有个.
故选:B.
【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
8.(2022 包头)几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4
C.6 D.9
【答案】B
【分析】根据该几何体的俯视图以及该位置小正方体的个数,可以画出左视图,从而求出左视图的面积;
【详解】由俯视图以及该位置小正方体的个数,左视图共有两列,第一列两个小正方体,第二列两个小正方体,可以画出左视图如图,所以这个几何体的左视图的面积为4故选:B
【点睛】本题考查了物体的三视图,解题饿到关键是根据俯视图,以及该位置小正方体的个数,正确作出左视图.
9.(2022·浙江金华·中考真题)如图,圆柱的底面直径为,高为,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
【答案】C
【分析】根据圆柱的侧面展开特征,两点之间线段最短判断即可;
【详解】解:∵AB为底面直径,
∴将圆柱侧面沿“剪开”后, B点在长方形上面那条边的中间,
∵两点之间线段最短,故选: C.
【点睛】本题考查了圆柱的侧面展开,掌握两点之间线段最短是解题关键.
题型三、正方体的展开与折叠
1.(2022·四川内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
【答案】C
【分析】根据正方体表面展开图的特征进行判断即可.
【详解】解:由正方体表面展开图的“相间、Z端是对面”可知,
“话”与“走”是对面,
故答案为:C.
【点睛】本题考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的前提.
2.(2022·湖北恩施)下图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是( )
A.“恩” B.“乡” C.“村” D.“兴”
【答案】D
【分析】根据正方体的平面展开图的特点即可得.
【详解】解:由正方体的平面展开图的特点得:“恩”字与“乡”字在相对面上,“施”字与“村”字在相对面上,“振”字与“兴”字在相对面上,
故选:D.
3.(2022·黑龙江绥化·中考真题)下列图形中,正方体展开图错误的是( )
A.B.C. D.
【答案】D
【分析】利用正方体及其表面展开图的特点解题.
【详解】D选项出现了“田字形”,折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,A、B、C选项是一个正方体的表面展开图.故选:D.
题型四、投影
1.(2022 靖西模拟)如图,小莉用灯泡O照射一个矩形硬纸片ABCD,在墙上形成矩形影子A′B′C′D′,现测得OA=2 cm,OA′=5 cm,纸片ABCD的面积为8 cm2,则影子A′B′C′D′的面积为 cm2.
【答案】50
2.(2022·广西)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是________米.
【答案】134
【分析】在同一时刻物高和影子成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,根据相似三角形的性质即可得.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:134.
【点睛】本题考查了相似三角形的应用,解题的关键是了解:同一时刻物高和影长成正比.
3.(2022·浙江温州·中考真题)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于___________米.转动时,叶片外端离地面的最大高度等于___________米.
【答案】 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,由题意可知,点O是AB的中点,
∵,∴点H是CD的中点,
∵,∴,
∴,
又∵由题意可知:,∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,∴,
∵由题意可知:,
又∵,∴,
∴,∴,∴,,
∵,∴四边形IHDJ是平行四边形,∴,
∵,∴,,,
∵在中,由勾股定理得:,
∴,∴,
∴,
∴叶片外端离地面的最大高度等于,故答案为:10,.
【点睛】本题主要考查了投影和相似的应用,及勾股定理和平行四边形的判定与性质,正确作出辅助线是解答本题的关键.
4.(2022·陕西·中考真题)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
【答案】旗杆的高AB为3米.
【分析】证明△AOD∽△EFG,利用相似比计算出AO的长,再证明△BOC∽△AOD,然后利用相似比计算OB的长,进一步计算即可求解.
【详解】解:∵AD∥EG,∴∠ADO=∠EGF.
又∵∠AOD=∠EFG=90°,∴△AOD∽△EFG.
∴.∴.
同理,△BOC∽△AOD.∴.∴.
∴AB=OA OB=3(米).∴旗杆的高AB为3米.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.
同课章节目录
