【模块六 圆】专题2 与圆有关的位置关系-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块六 圆】专题2 与圆有关的位置关系-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 20:32:44 | ||
图片预览


文档简介
2023年中考数学第一轮复习
模块六 圆
专题2 与圆有关的位置关系
与圆有关的位置关系 点、与圆的位置关系 如果圆的半径为r,某一点到圆心的距离为d,那么: (1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d线与圆的位置关系 .直线与圆的位置关系有三种:相离、相切和相交 位置 关系相离相切相交图形公共点个数012数量关系d>rd=rd切线 性质 圆的切线垂直于经过切点的半径.
判定 经过半径的外端并且垂直于这条半径的直线是圆的切线.
证明切线的常用方法 1.已知直线过半径外端,证直角; 2.已知直线与圆有公共点,连半径,证直角; 3.直线与圆没有明确的公共点,作垂线段,证半径.
切线长 定义 经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
题型一、点与圆、直线与圆的位置关系
1.(2022·吉林)如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
2.(2021 嘉兴)已知平面内有⊙O和点A,B,若⊙O半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与⊙O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
题型二、切线的性质与判定
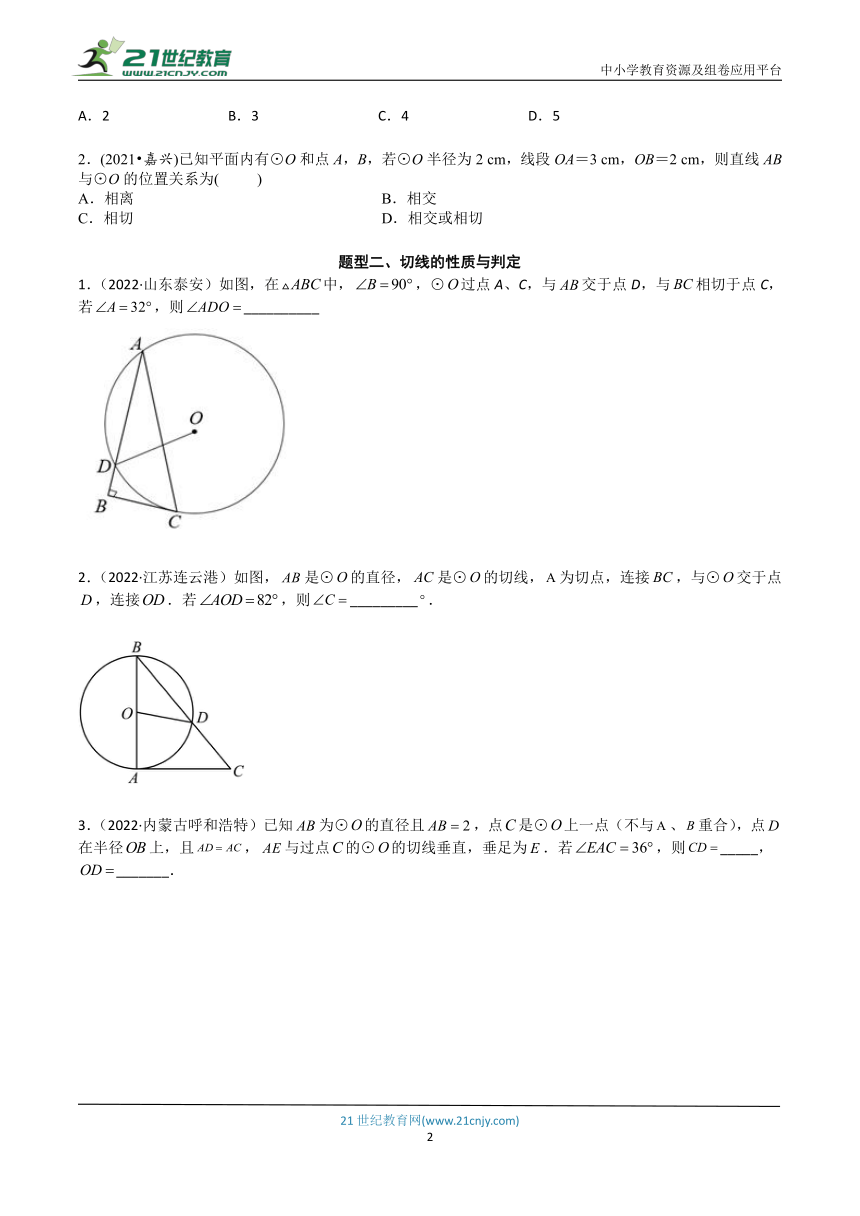
1.(2022·山东泰安)如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
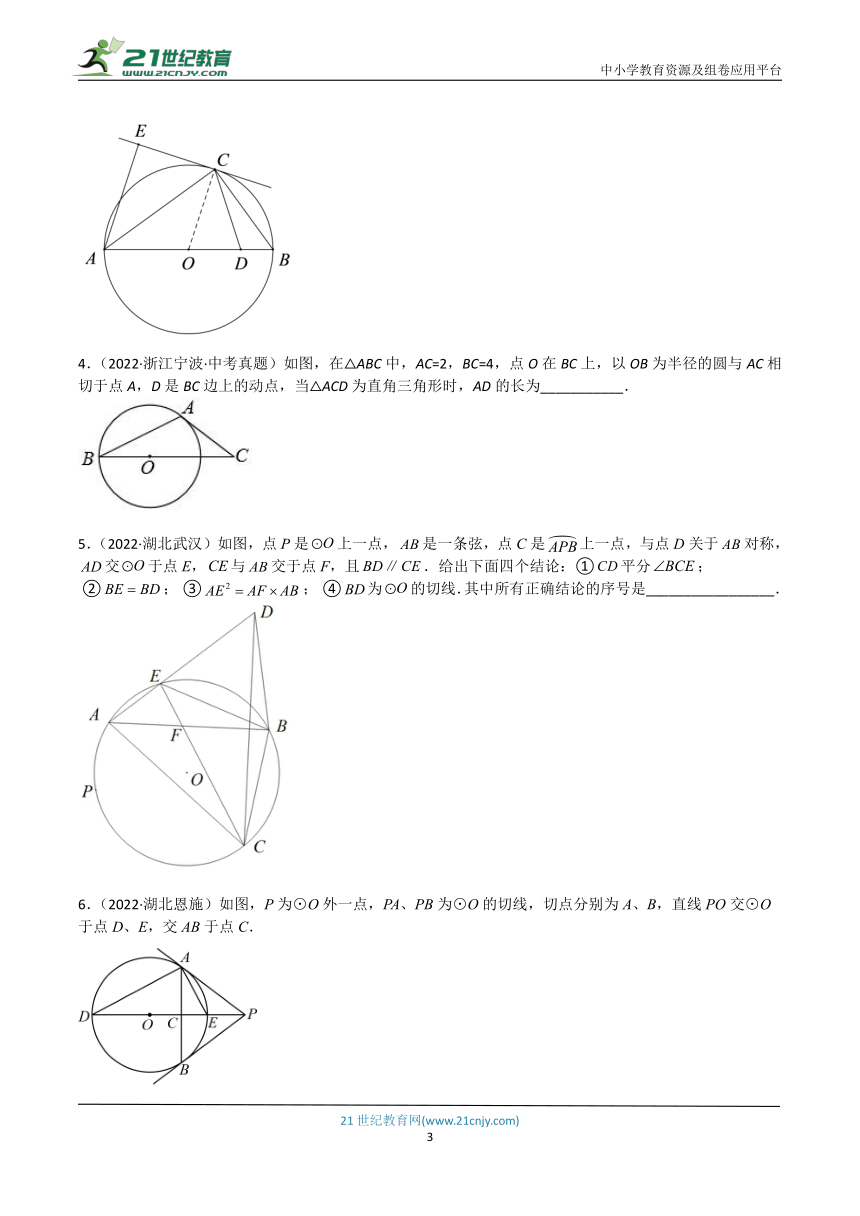
2.(2022·江苏连云港)如图,是⊙的直径,是⊙的切线,为切点,连接,与⊙交于点,连接.若,则_________.
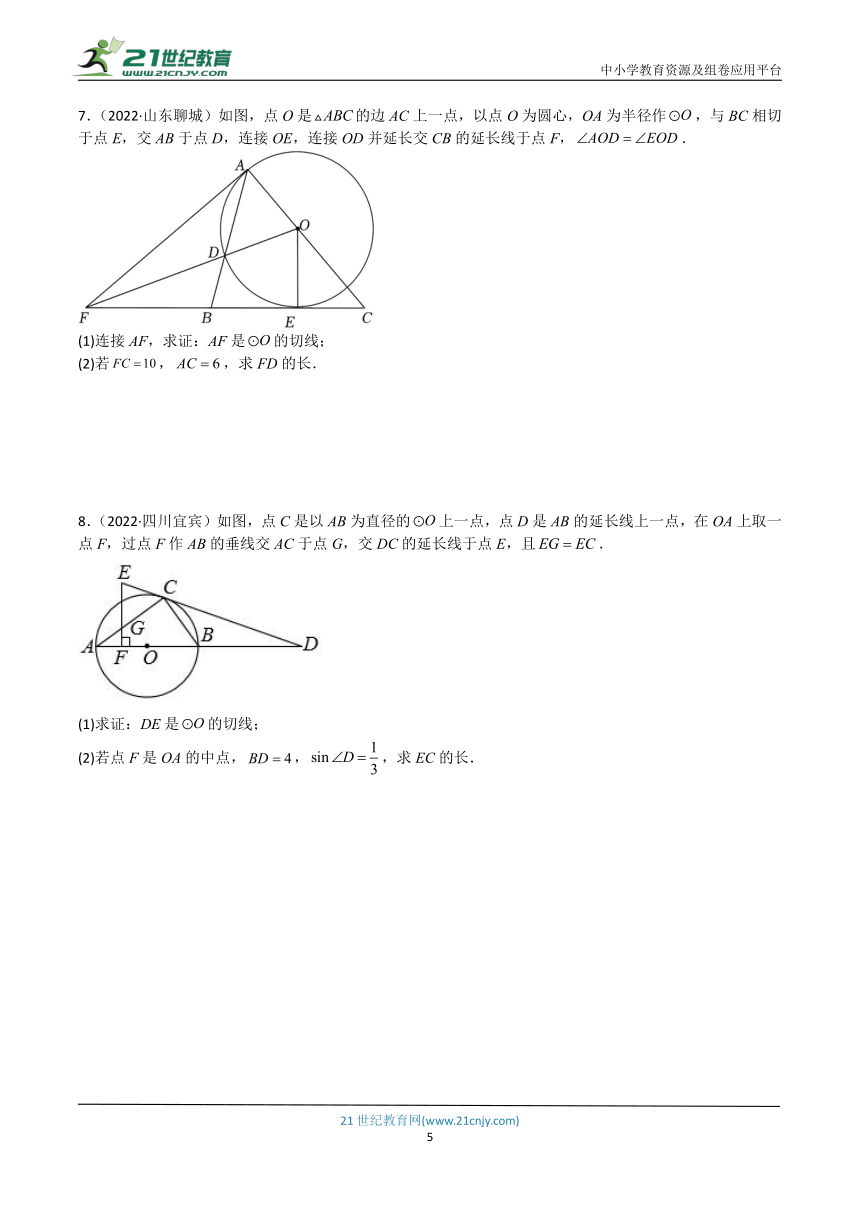
3.(2022·内蒙古呼和浩特)已知为⊙的直径且,点是⊙上一点(不与、重合),点在半径上,且,与过点的⊙的切线垂直,垂足为.若,则_____,_______.
4.(2022·浙江宁波·中考真题)如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A,D是BC边上的动点,当△ACD为直角三角形时,AD的长为___________.
5.(2022·湖北武汉)如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分;
②; ③; ④为的切线.其中所有正确结论的序号是_________________.
6.(2022·湖北恩施)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)求证:∠ADE=∠PAE.
(2)若∠ADE=30°,求证:AE=PE.
(3)若PE=4,CD=6,求CE的长.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
7.(2022·山东聊城)如图,点O是的边AC上一点,以点O为圆心,OA为半径作,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,.
(1)连接AF,求证:AF是的切线;
(2)若,,求FD的长.
8.(2022·四川宜宾)如图,点C是以AB为直径的上一点,点D是AB的延长线上一点,在OA上取一点F,过点F作AB的垂线交AC于点G,交DC的延长线于点E,且.
(1)求证:DE是的切线;
(2)若点F是OA的中点,,,求EC的长.
9.(2022·湖北十堰)如图,中,,为上一点,以为直径的与相切于点,交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
10.(2022·湖南郴州)如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
11.(2022·四川雅安)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.
(1)求证:AB是⊙O的切线;
(2)连接CE,求证:△ACE∽△ADC;
(3)若=,⊙O的半径为6,求tan∠OAC.
12.(2022·广西贵港)图,在中,,点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)求证:是⊙的切线;
(2)若,,求⊙的半径及的长.
题型三、切线长定理及其应用
1.(2022·湖北恩施)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
2.(2022·湖北武汉·中考真题)如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
3.(2022·山东泰安·中考真题)如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
2023年中考数学第一轮复习
模块六 圆
专题2 与圆有关的位置关系
与圆有关的位置关系 点、与圆的位置关系 如果圆的半径为r,某一点到圆心的距离为d,那么: (1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d线与圆的位置关系 .直线与圆的位置关系有三种:相离、相切和相交 位置 关系相离相切相交图形公共点个数012数量 关系d>rd=rd切线 性质 圆的切线垂直于经过切点的半径.
判定 经过半径的外端并且垂直于这条半径的直线是圆的切线.
证明切线的常用方法 1.已知直线过半径外端,证直角; 2.已知直线与圆有公共点,连半径,证直角; 3.直线与圆没有明确的公共点,作垂线段,证半径.
切线长 定义 经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
题型一、点与圆、直线与圆的位置关系
1.(2022·吉林)如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
【答案】C
【分析】先利用勾股定理可得,再根据“点在内且点在外”可得,由此即可得出答案.
【详解】解:在中,,,,
,
点在内且点在外,
,即,
观察四个选项可知,只有选项C符合,故选:C.
【点睛】本题考查了勾股定理、点与圆的位置关系,熟练掌握点与圆的位置关系是解题关键.
2.(2021 嘉兴)已知平面内有⊙O和点A,B,若⊙O半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与⊙O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
【答案】D
题型二、切线的性质与判定
1.(2022·山东泰安)如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
【答案】##64度
【分析】根据同弧对应的圆心角是圆周角的2倍计算出,再根据,内错角得到答案.
【详解】如下图所示,连接OC
从图中可以看出,是圆弧对应的圆周角,是圆弧对应的圆心角
得.
∵BC是圆O的切线
∴
∵
∴
∴
∴
故答案为:.
【点睛】本题考查圆的切线的性质,圆周角定理、平行线的判定和性质,解题的关键是熟练掌握圆和平行线的相关知识.
2.(2022·江苏连云港)如图,是⊙的直径,是⊙的切线,为切点,连接,与⊙交于点,连接.若,则_________.
【答案】49
【分析】利用同弧所对的圆周角等于圆心角的一半求得∠B=∠AOD=41°,根据AC是⊙O的切线得到∠BAC=90°,即可求出答案.
【详解】解:∵∠AOD=82°,
∴∠B=∠AOD=41°,
∵AC为圆的切线,A为切点,
∴∠BAC=90°,
∴∠C=90°-41°=49°
故答案为49.
【点睛】此题考查圆周角定理,圆的切线的性质定理,直角三角形两锐角互余,正确理解圆周角定理及切线的性质定理是解题的关键.
3.(2022·内蒙古呼和浩特)已知为⊙的直径且,点是⊙上一点(不与、重合),点在半径上,且,与过点的⊙的切线垂直,垂足为.若,则_____,_______.
【答案】 1
【分析】根据题意作出图形,连接,根据切线的性质,等边对等角,平行线的性质可得,根据,可得,可得,进而证明,根据相似三角形的性质列出方程,解方程即可求解.
【详解】如图,连接,
是⊙的切线,,,
,
,
,
,
,
,
,
,
,
,
,
设,则
解得(舍去)
即
故答案为:.
【点睛】本题考查了切线的性质,等腰三角形的性质与判定,相似三角形的性质与判定,综合运用以上知识结合图形求解是解题的关键.
4.(2022·浙江宁波·中考真题)如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A,D是BC边上的动点,当△ACD为直角三角形时,AD的长为___________.
【答案】或
【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可.
【详解】解:连接OA,
①当D点与O点重合时,∠CAD为90°,设圆的半径=r,∴OA=r,OC=4-r,
∵AC=4,在Rt△AOC中,根据勾股定理可得:r2+4=(4-r)2,解得:r=,即AD=AO=;
②当∠ADC=90°时,过点A作AD⊥BC于点D,
∵AO AC=OC AD,∴AD=,∵AO=,AC=2,OC=4-r=,∴AD=,
综上所述,AD的长为或,故答案为:或.
【点睛】本题主要考查了切线的性质和勾股定理,熟练掌握这些性质定理是解决本题的关键.
5.(2022·湖北武汉)如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是_________________.
【答案】①②④
【分析】根据点AB为CD的垂直平分线,得出BD=BC,AD=AC,根据等边对等角得出∠BDC=∠BCD,利用平行线性质可判断①正确;利用△ADB≌△ACB(SSS)得出∠EAB=∠CAB,利用圆周角弧与弦关系可判断②正确;根据等弧所对的圆周角相等可得∠AEF≠∠ABE,从而可得△AEF与△ABE不相似,即可判断③;连结OB,利用垂径定理得出OB⊥CE,利用平行线性质得出OB⊥BD,即可判断④正确.
【详解】解:∵点C是上一点,与点D关于对称,
∴AB为CD的垂直平分线,
∴BD=BC,AD=AC,
∴∠BDC=∠BCD,
∵,
∴∠ECD=∠CDB,
∴∠ECD=∠BCD,
∴CD平分∠BCE,故①正确;
在△ADB和△ACB中,
∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB(SSS),
∴∠EAB=∠CAB,
∴,
∴BE=BC=BD,故②正确;
∵AC≠AE,
∴≠,
∴∠AEF≠∠ABE,
∴△AEF与△ABE不相似,故③错误;
连结OB,
∵,CE为弦,
∴OB⊥CE,
∵,
∴OB⊥BD,
∴BD为的切线.故④正确,
∴其中所有正确结论的序号是①②④.
故答案为①②④.
.
【点睛】本题考查轴对称性质,线段垂直平分线性质,角平分线判定,三角形全等判断于性质,垂径定理,切线判断,掌握轴对称性质,线段垂直平分线性质,角平分线判定,三角形全等判断于性质,垂径定理,切线判断是解题关键.
6.(2022·湖北恩施)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)求证:∠ADE=∠PAE.(2)若∠ADE=30°,求证:AE=PE.(3)若PE=4,CD=6,求CE的长.
【答案】(1)见解析(2)见解析(3)CE的长为2.
【分析】(1)连接OA,根据切线的性质得到∠OAE+∠PAE=90°,根据圆周角定理得到∠OAE+∠DAO=90°,据此即可证明∠ADE=∠PAE;
(2)由(1)得∠ADE=∠PAE =30°,∠AED =60°,利用三角形外角的性质得到∠APE=∠AED-∠PAE =30°,再根据等角对等边即可证明AE=PE;
(3)证明Rt△EAC∽Rt△ADC,Rt△OAC∽Rt△APC,推出DC×CE=OC×PC,设CE=x,据此列方程求解即可.
(1)证明:连接OA,
∵PA为⊙O的切线,
∴OA⊥PA,即∠OAP=90°,
∴∠OAE+∠PAE=90°,
∵DE为⊙O的直径,
∴∠DAE=90°,即∠OAE+∠DAO=90°,
∴∠DAO=∠PAE,
∵OA=OD,
∴∠DAO=∠ADE,
∴∠ADE=∠PAE;
(2)证明:∵∠ADE=30°,
由(1)得∠ADE=∠PAE =30°,∠AED=90°-∠ADE=60°,
∴∠APE=∠AED-∠PAE =30°,
∴∠APE=∠PAE =30°,
∴AE=PE;
(3)解:∵PA、PB为⊙O的切线,切点分别为A、B,直线PO交AB于点C.
∴AB⊥PD,
∵∠DAE=90°,∠OAP=90°,
∴∠DAC+∠CAE=90°,∠OAC+∠PAC=90°,
∵∠DAC+∠D=90°,∠OAC+∠AOC=90°,
∴∠CAE=∠D,∠PAC=∠AOC,
∴Rt△EAC∽Rt△ADC,Rt△OAC∽Rt△APC,
∴AC2=DC×CE,AC2=OC×PC,
即DC×CE=OC×PC,
设CE=x,则DE=6+x,OE=3+,OC=3+-x=3-,PC=4+x,
∴6x=(3-)( 4+x),
整理得:x2+10x-24=0,
解得:x=2(负值已舍).
∴CE的长为2.
【点睛】本题考查了切线的性质,相似三角形的判定和性质,圆周角定理,解题的关键是学会利用参数构建方程解决问题.
7.(2022·山东聊城)如图,点O是的边AC上一点,以点O为圆心,OA为半径作,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,.
(1)连接AF,求证:AF是的切线;(2)若,,求FD的长.
【答案】(1)见解析(2)FD的长为
【分析】(1)根据SAS证△AOF≌△EOF,得出∠OAF=∠OEF=90°,即可得出结论;
(2)根据勾股定理求出AF,证△OEC∽△FAC,设圆O的半径为r,根据线段比例关系列方程求出r,利用勾股定理求出OF,最后根据FD=OF﹣OD求出即可.
(1)证明:在△AOF和△EOF中,
,
∴△AOF≌△EOF(SAS),
∴∠OAF=∠OEF,
∵BC与相切,
∴OE⊥FC,
∴∠OAF=∠OEF=90°,
即OA⊥AF,
∵OA是的半径,
∴AF是的切线;
(2)
解:在中,∠CAF=90°,FC=10,AC=6,
∴,
∵BC与相切,AF是的切线
∴∠OEC=∠FAC=∠90°,
∵∠OCE=∠FCA,
∴△OEC∽△FAC,
∴,
设的半径为r,则,
解得,
在Rt△FAO中,∠FAO=90°,AF=8,,
∴,
∴,
即FD的长为.
【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,熟练掌握切线的判定和性质是解题的关键.
8.(2022·四川宜宾)如图,点C是以AB为直径的上一点,点D是AB的延长线上一点,在OA上取一点F,过点F作AB的垂线交AC于点G,交DC的延长线于点E,且.
(1)求证:DE是的切线;
(2)若点F是OA的中点,,,求EC的长.
【答案】(1)见解析
(2)
【分析】(1)连结OC,利用等腰三角形的性质和圆周角定理证,即可由切线的判定定理得出结论;
(2)解,求出,从而求得,则可求得,再证,得,即可求得,即可由求解.
(1)
证明:如图,连结OC,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,即,
∴,
∴DE是的切线;
(2)
解:在中,,,
∴,
∴,
∴,
∴,
又∵点F为AO中点,
∴,
∴,
∵,
∴,
∴,即,
∴,
∴.
【点睛】本题考查切线的判定,圆周角定理,等腰三角形的性质,解直角三角形,相似三角形的判定与性质,熟练掌握相关性质与判定是解题的关键.
9.(2022·湖北十堰)如图,中,,为上一点,以为直径的与相切于点,交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,设,,根据已知条件以及直径所对的圆周角相等,证明,进而求得,即可证明是的切线;
(2)根据已知条件结合(1)的结论可得四边形是正方形,进而求得的长,根据,,即可求解.
(1)
如图,连接,
,
则,
设,,
,
,
为的直径,
,
,
即,
,
,
,
,
,
,
,
为的半径,
是的切线;
(2)
如图,连接,
是的切线,则,又,
四边形是矩形,
,
四边形是正方形,
,
在中,,,
,
,
由(1)可得,
,
,
,
解得 .
【点睛】本题考查了切线的性质与判定,正方形的性质与判定,等腰三角形的性质,正弦的定义,掌握切线的性质与判定是解题的关键.
10.(2022·湖南郴州)如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
【答案】(1)见解析
(2)3
【分析】(1)连接AD、OD,根据等腰三角形的性质可证得,根据平行线的判定与性质可证得,然后根据切线的判定即可证得结论;
(2)根据含30°角的直角三角形的性质求得CD、CE 即可.
(1)
证明:连接AD、OD,记,,
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴,
∴,
∴,
又∵OD是⊙O的半径,
∴直线PE是⊙O的切线.
(2)
连接AD,
∵AB是直径,
∴,
∴.
又∵,
∴,
∵,,
∴,
又∵,
∴为等边三角形,
∴,,
∴,
在中,∵,
∴.
【点睛】本题考查等腰三角形的性质、平行线的判定与性质、切线的判定、等边三角形的判定与性质、解直角三角形,难度适中,熟练掌握相关知识的联系与运用是解答的关键.
11.(2022·四川雅安)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.
(1)求证:AB是⊙O的切线;
(2)连接CE,求证:△ACE∽△ADC;
(3)若=,⊙O的半径为6,求tan∠OAC.
【答案】(1)证明见解析
(2)证明见解析
(3)tan∠OAC
【分析】(1)如图,过作于证明 即可得到结论;
(2)证明 再结合 从而可得结论;
(3)由相似三角形的性质可得 设 则 而 从而建立方程求解x,从而可得答案.
(1)
证明:如图,过作于
∠ACB=90°,AO是△ABC的角平分线,
O为圆心,OC为半径,
是⊙O的切线.
(2)
如图,连结CE,
为的直径,
(3)
设 则 而
解得
tan∠OAC
【点睛】本题考查的是切线的判定,相似三角形的判定与性质,求解锐角的正切,证明,利用相似三角形的性质求解是解本题的关键.
12.(2022·广西贵港)图,在中,,点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)求证:是⊙的切线;
(2)若,,求⊙的半径及的长.
【答案】(1)见解析
(2),
【分析】(1)作,垂足为H,连接,先证明是的平分线,然后由切线的判定定理进行证明,即可得到结论成立;
(2)设,由勾股定理可求,设的半径为r,然后证明,结合勾股定理即可求出答案.
(1)
证明:如图,作,垂足为H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴∠BDC=2∠FAC,
∴,即是的平分线,
∵O在上,与相切于点E,
∴,且是的半径,
∵AC平分∠FAB,OH⊥AF,
∴是的半径,
∴是的切线.
(2)
解:如(1)图,∵在中,,
∴可设,
∴,
则,
设的半径为r,则,
∵,
∴,
∴,即,则,
在Rt△AOE中,AO=5,OE=3,
由勾股定理得,又,
∴,
在中,由勾股定理得:.
【点睛】本题考查了三角函数,切线的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行证明.
题型三、切线长定理及其应用
1.(2022·湖北恩施)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
【答案】-
【分析】利用切线长定理求得⊙O的半径,根据S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE列式计算即可求解.
【详解】解:设切点分别为D、E、F,连接OD、OE、OF,
∵⊙O为Rt△ABC的内切圆,
∴AE=AF、BD=BF、CD=CE,OD⊥BC,OE⊥AC,
∵∠C=90°,
∴四边形CDOE为正方形,
∴∠EOF+∠FOD=360°-90°=270°,
设⊙O的半径为x,则CD=CE=x,AE=AF=4-x,BD=BF=3-x,
∴4-x+3-x=5,
解得x=1,
∴S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE
=×3×4-×1×1
=-.
故答案为:-.
【点睛】本题考查了切线长定理,扇形的面积公式,熟记各图形的性质并准确识图是解题的关键.
2.(2022·湖北武汉·中考真题)如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
【答案】B
【分析】如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,据此求解即可.
【详解】解:如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,
∵,∠BAD=90°,
∴△EAD∽△EBC,∠B=90°,
∴,即,
∴,
∴EB=32cm,
∴,
设这个圆的圆心为O,与EB,BC,EC分别相切于F,G,H,
∴OF=OG=OH,
∵,
∴,
∴,
∴,
∴此圆的半径为8cm,
故选B.
【点睛】本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.
3.(2022·山东泰安·中考真题)如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】C
【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是△ACM的中位线即可解决问题.
【详解】解:延长ID到M,使DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,
∵AE=EC,
∴IE是△ACM的中位线,
∴IE=CM=4,故选:C.
【点睛】本题考查三角形的内心、三角形的外接圆、三角形的中位线定理、直角三角形的判定、勾股定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题.
模块六 圆
专题2 与圆有关的位置关系
与圆有关的位置关系 点、与圆的位置关系 如果圆的半径为r,某一点到圆心的距离为d,那么: (1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d
判定 经过半径的外端并且垂直于这条半径的直线是圆的切线.
证明切线的常用方法 1.已知直线过半径外端,证直角; 2.已知直线与圆有公共点,连半径,证直角; 3.直线与圆没有明确的公共点,作垂线段,证半径.
切线长 定义 经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
题型一、点与圆、直线与圆的位置关系
1.(2022·吉林)如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
2.(2021 嘉兴)已知平面内有⊙O和点A,B,若⊙O半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与⊙O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
题型二、切线的性质与判定
1.(2022·山东泰安)如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
2.(2022·江苏连云港)如图,是⊙的直径,是⊙的切线,为切点,连接,与⊙交于点,连接.若,则_________.
3.(2022·内蒙古呼和浩特)已知为⊙的直径且,点是⊙上一点(不与、重合),点在半径上,且,与过点的⊙的切线垂直,垂足为.若,则_____,_______.
4.(2022·浙江宁波·中考真题)如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A,D是BC边上的动点,当△ACD为直角三角形时,AD的长为___________.
5.(2022·湖北武汉)如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分;
②; ③; ④为的切线.其中所有正确结论的序号是_________________.
6.(2022·湖北恩施)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)求证:∠ADE=∠PAE.
(2)若∠ADE=30°,求证:AE=PE.
(3)若PE=4,CD=6,求CE的长.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
7.(2022·山东聊城)如图,点O是的边AC上一点,以点O为圆心,OA为半径作,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,.
(1)连接AF,求证:AF是的切线;
(2)若,,求FD的长.
8.(2022·四川宜宾)如图,点C是以AB为直径的上一点,点D是AB的延长线上一点,在OA上取一点F,过点F作AB的垂线交AC于点G,交DC的延长线于点E,且.
(1)求证:DE是的切线;
(2)若点F是OA的中点,,,求EC的长.
9.(2022·湖北十堰)如图,中,,为上一点,以为直径的与相切于点,交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
10.(2022·湖南郴州)如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
11.(2022·四川雅安)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.
(1)求证:AB是⊙O的切线;
(2)连接CE,求证:△ACE∽△ADC;
(3)若=,⊙O的半径为6,求tan∠OAC.
12.(2022·广西贵港)图,在中,,点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)求证:是⊙的切线;
(2)若,,求⊙的半径及的长.
题型三、切线长定理及其应用
1.(2022·湖北恩施)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
2.(2022·湖北武汉·中考真题)如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
3.(2022·山东泰安·中考真题)如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
2023年中考数学第一轮复习
模块六 圆
专题2 与圆有关的位置关系
与圆有关的位置关系 点、与圆的位置关系 如果圆的半径为r,某一点到圆心的距离为d,那么: (1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d
判定 经过半径的外端并且垂直于这条半径的直线是圆的切线.
证明切线的常用方法 1.已知直线过半径外端,证直角; 2.已知直线与圆有公共点,连半径,证直角; 3.直线与圆没有明确的公共点,作垂线段,证半径.
切线长 定义 经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
题型一、点与圆、直线与圆的位置关系
1.(2022·吉林)如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
【答案】C
【分析】先利用勾股定理可得,再根据“点在内且点在外”可得,由此即可得出答案.
【详解】解:在中,,,,
,
点在内且点在外,
,即,
观察四个选项可知,只有选项C符合,故选:C.
【点睛】本题考查了勾股定理、点与圆的位置关系,熟练掌握点与圆的位置关系是解题关键.
2.(2021 嘉兴)已知平面内有⊙O和点A,B,若⊙O半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与⊙O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
【答案】D
题型二、切线的性质与判定
1.(2022·山东泰安)如图,在中,,⊙过点A、C,与交于点D,与相切于点C,若,则__________
【答案】##64度
【分析】根据同弧对应的圆心角是圆周角的2倍计算出,再根据,内错角得到答案.
【详解】如下图所示,连接OC
从图中可以看出,是圆弧对应的圆周角,是圆弧对应的圆心角
得.
∵BC是圆O的切线
∴
∵
∴
∴
∴
故答案为:.
【点睛】本题考查圆的切线的性质,圆周角定理、平行线的判定和性质,解题的关键是熟练掌握圆和平行线的相关知识.
2.(2022·江苏连云港)如图,是⊙的直径,是⊙的切线,为切点,连接,与⊙交于点,连接.若,则_________.
【答案】49
【分析】利用同弧所对的圆周角等于圆心角的一半求得∠B=∠AOD=41°,根据AC是⊙O的切线得到∠BAC=90°,即可求出答案.
【详解】解:∵∠AOD=82°,
∴∠B=∠AOD=41°,
∵AC为圆的切线,A为切点,
∴∠BAC=90°,
∴∠C=90°-41°=49°
故答案为49.
【点睛】此题考查圆周角定理,圆的切线的性质定理,直角三角形两锐角互余,正确理解圆周角定理及切线的性质定理是解题的关键.
3.(2022·内蒙古呼和浩特)已知为⊙的直径且,点是⊙上一点(不与、重合),点在半径上,且,与过点的⊙的切线垂直,垂足为.若,则_____,_______.
【答案】 1
【分析】根据题意作出图形,连接,根据切线的性质,等边对等角,平行线的性质可得,根据,可得,可得,进而证明,根据相似三角形的性质列出方程,解方程即可求解.
【详解】如图,连接,
是⊙的切线,,,
,
,
,
,
,
,
,
,
,
,
,
设,则
解得(舍去)
即
故答案为:.
【点睛】本题考查了切线的性质,等腰三角形的性质与判定,相似三角形的性质与判定,综合运用以上知识结合图形求解是解题的关键.
4.(2022·浙江宁波·中考真题)如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A,D是BC边上的动点,当△ACD为直角三角形时,AD的长为___________.
【答案】或
【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可.
【详解】解:连接OA,
①当D点与O点重合时,∠CAD为90°,设圆的半径=r,∴OA=r,OC=4-r,
∵AC=4,在Rt△AOC中,根据勾股定理可得:r2+4=(4-r)2,解得:r=,即AD=AO=;
②当∠ADC=90°时,过点A作AD⊥BC于点D,
∵AO AC=OC AD,∴AD=,∵AO=,AC=2,OC=4-r=,∴AD=,
综上所述,AD的长为或,故答案为:或.
【点睛】本题主要考查了切线的性质和勾股定理,熟练掌握这些性质定理是解决本题的关键.
5.(2022·湖北武汉)如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是_________________.
【答案】①②④
【分析】根据点AB为CD的垂直平分线,得出BD=BC,AD=AC,根据等边对等角得出∠BDC=∠BCD,利用平行线性质可判断①正确;利用△ADB≌△ACB(SSS)得出∠EAB=∠CAB,利用圆周角弧与弦关系可判断②正确;根据等弧所对的圆周角相等可得∠AEF≠∠ABE,从而可得△AEF与△ABE不相似,即可判断③;连结OB,利用垂径定理得出OB⊥CE,利用平行线性质得出OB⊥BD,即可判断④正确.
【详解】解:∵点C是上一点,与点D关于对称,
∴AB为CD的垂直平分线,
∴BD=BC,AD=AC,
∴∠BDC=∠BCD,
∵,
∴∠ECD=∠CDB,
∴∠ECD=∠BCD,
∴CD平分∠BCE,故①正确;
在△ADB和△ACB中,
∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB(SSS),
∴∠EAB=∠CAB,
∴,
∴BE=BC=BD,故②正确;
∵AC≠AE,
∴≠,
∴∠AEF≠∠ABE,
∴△AEF与△ABE不相似,故③错误;
连结OB,
∵,CE为弦,
∴OB⊥CE,
∵,
∴OB⊥BD,
∴BD为的切线.故④正确,
∴其中所有正确结论的序号是①②④.
故答案为①②④.
.
【点睛】本题考查轴对称性质,线段垂直平分线性质,角平分线判定,三角形全等判断于性质,垂径定理,切线判断,掌握轴对称性质,线段垂直平分线性质,角平分线判定,三角形全等判断于性质,垂径定理,切线判断是解题关键.
6.(2022·湖北恩施)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)求证:∠ADE=∠PAE.(2)若∠ADE=30°,求证:AE=PE.(3)若PE=4,CD=6,求CE的长.
【答案】(1)见解析(2)见解析(3)CE的长为2.
【分析】(1)连接OA,根据切线的性质得到∠OAE+∠PAE=90°,根据圆周角定理得到∠OAE+∠DAO=90°,据此即可证明∠ADE=∠PAE;
(2)由(1)得∠ADE=∠PAE =30°,∠AED =60°,利用三角形外角的性质得到∠APE=∠AED-∠PAE =30°,再根据等角对等边即可证明AE=PE;
(3)证明Rt△EAC∽Rt△ADC,Rt△OAC∽Rt△APC,推出DC×CE=OC×PC,设CE=x,据此列方程求解即可.
(1)证明:连接OA,
∵PA为⊙O的切线,
∴OA⊥PA,即∠OAP=90°,
∴∠OAE+∠PAE=90°,
∵DE为⊙O的直径,
∴∠DAE=90°,即∠OAE+∠DAO=90°,
∴∠DAO=∠PAE,
∵OA=OD,
∴∠DAO=∠ADE,
∴∠ADE=∠PAE;
(2)证明:∵∠ADE=30°,
由(1)得∠ADE=∠PAE =30°,∠AED=90°-∠ADE=60°,
∴∠APE=∠AED-∠PAE =30°,
∴∠APE=∠PAE =30°,
∴AE=PE;
(3)解:∵PA、PB为⊙O的切线,切点分别为A、B,直线PO交AB于点C.
∴AB⊥PD,
∵∠DAE=90°,∠OAP=90°,
∴∠DAC+∠CAE=90°,∠OAC+∠PAC=90°,
∵∠DAC+∠D=90°,∠OAC+∠AOC=90°,
∴∠CAE=∠D,∠PAC=∠AOC,
∴Rt△EAC∽Rt△ADC,Rt△OAC∽Rt△APC,
∴AC2=DC×CE,AC2=OC×PC,
即DC×CE=OC×PC,
设CE=x,则DE=6+x,OE=3+,OC=3+-x=3-,PC=4+x,
∴6x=(3-)( 4+x),
整理得:x2+10x-24=0,
解得:x=2(负值已舍).
∴CE的长为2.
【点睛】本题考查了切线的性质,相似三角形的判定和性质,圆周角定理,解题的关键是学会利用参数构建方程解决问题.
7.(2022·山东聊城)如图,点O是的边AC上一点,以点O为圆心,OA为半径作,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,.
(1)连接AF,求证:AF是的切线;(2)若,,求FD的长.
【答案】(1)见解析(2)FD的长为
【分析】(1)根据SAS证△AOF≌△EOF,得出∠OAF=∠OEF=90°,即可得出结论;
(2)根据勾股定理求出AF,证△OEC∽△FAC,设圆O的半径为r,根据线段比例关系列方程求出r,利用勾股定理求出OF,最后根据FD=OF﹣OD求出即可.
(1)证明:在△AOF和△EOF中,
,
∴△AOF≌△EOF(SAS),
∴∠OAF=∠OEF,
∵BC与相切,
∴OE⊥FC,
∴∠OAF=∠OEF=90°,
即OA⊥AF,
∵OA是的半径,
∴AF是的切线;
(2)
解:在中,∠CAF=90°,FC=10,AC=6,
∴,
∵BC与相切,AF是的切线
∴∠OEC=∠FAC=∠90°,
∵∠OCE=∠FCA,
∴△OEC∽△FAC,
∴,
设的半径为r,则,
解得,
在Rt△FAO中,∠FAO=90°,AF=8,,
∴,
∴,
即FD的长为.
【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,熟练掌握切线的判定和性质是解题的关键.
8.(2022·四川宜宾)如图,点C是以AB为直径的上一点,点D是AB的延长线上一点,在OA上取一点F,过点F作AB的垂线交AC于点G,交DC的延长线于点E,且.
(1)求证:DE是的切线;
(2)若点F是OA的中点,,,求EC的长.
【答案】(1)见解析
(2)
【分析】(1)连结OC,利用等腰三角形的性质和圆周角定理证,即可由切线的判定定理得出结论;
(2)解,求出,从而求得,则可求得,再证,得,即可求得,即可由求解.
(1)
证明:如图,连结OC,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,即,
∴,
∴DE是的切线;
(2)
解:在中,,,
∴,
∴,
∴,
∴,
又∵点F为AO中点,
∴,
∴,
∵,
∴,
∴,即,
∴,
∴.
【点睛】本题考查切线的判定,圆周角定理,等腰三角形的性质,解直角三角形,相似三角形的判定与性质,熟练掌握相关性质与判定是解题的关键.
9.(2022·湖北十堰)如图,中,,为上一点,以为直径的与相切于点,交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,设,,根据已知条件以及直径所对的圆周角相等,证明,进而求得,即可证明是的切线;
(2)根据已知条件结合(1)的结论可得四边形是正方形,进而求得的长,根据,,即可求解.
(1)
如图,连接,
,
则,
设,,
,
,
为的直径,
,
,
即,
,
,
,
,
,
,
,
为的半径,
是的切线;
(2)
如图,连接,
是的切线,则,又,
四边形是矩形,
,
四边形是正方形,
,
在中,,,
,
,
由(1)可得,
,
,
,
解得 .
【点睛】本题考查了切线的性质与判定,正方形的性质与判定,等腰三角形的性质,正弦的定义,掌握切线的性质与判定是解题的关键.
10.(2022·湖南郴州)如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
【答案】(1)见解析
(2)3
【分析】(1)连接AD、OD,根据等腰三角形的性质可证得,根据平行线的判定与性质可证得,然后根据切线的判定即可证得结论;
(2)根据含30°角的直角三角形的性质求得CD、CE 即可.
(1)
证明:连接AD、OD,记,,
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴,
∴,
∴,
又∵OD是⊙O的半径,
∴直线PE是⊙O的切线.
(2)
连接AD,
∵AB是直径,
∴,
∴.
又∵,
∴,
∵,,
∴,
又∵,
∴为等边三角形,
∴,,
∴,
在中,∵,
∴.
【点睛】本题考查等腰三角形的性质、平行线的判定与性质、切线的判定、等边三角形的判定与性质、解直角三角形,难度适中,熟练掌握相关知识的联系与运用是解答的关键.
11.(2022·四川雅安)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.
(1)求证:AB是⊙O的切线;
(2)连接CE,求证:△ACE∽△ADC;
(3)若=,⊙O的半径为6,求tan∠OAC.
【答案】(1)证明见解析
(2)证明见解析
(3)tan∠OAC
【分析】(1)如图,过作于证明 即可得到结论;
(2)证明 再结合 从而可得结论;
(3)由相似三角形的性质可得 设 则 而 从而建立方程求解x,从而可得答案.
(1)
证明:如图,过作于
∠ACB=90°,AO是△ABC的角平分线,
O为圆心,OC为半径,
是⊙O的切线.
(2)
如图,连结CE,
为的直径,
(3)
设 则 而
解得
tan∠OAC
【点睛】本题考查的是切线的判定,相似三角形的判定与性质,求解锐角的正切,证明,利用相似三角形的性质求解是解本题的关键.
12.(2022·广西贵港)图,在中,,点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)求证:是⊙的切线;
(2)若,,求⊙的半径及的长.
【答案】(1)见解析
(2),
【分析】(1)作,垂足为H,连接,先证明是的平分线,然后由切线的判定定理进行证明,即可得到结论成立;
(2)设,由勾股定理可求,设的半径为r,然后证明,结合勾股定理即可求出答案.
(1)
证明:如图,作,垂足为H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴∠BDC=2∠FAC,
∴,即是的平分线,
∵O在上,与相切于点E,
∴,且是的半径,
∵AC平分∠FAB,OH⊥AF,
∴是的半径,
∴是的切线.
(2)
解:如(1)图,∵在中,,
∴可设,
∴,
则,
设的半径为r,则,
∵,
∴,
∴,即,则,
在Rt△AOE中,AO=5,OE=3,
由勾股定理得,又,
∴,
在中,由勾股定理得:.
【点睛】本题考查了三角函数,切线的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行证明.
题型三、切线长定理及其应用
1.(2022·湖北恩施)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
【答案】-
【分析】利用切线长定理求得⊙O的半径,根据S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE列式计算即可求解.
【详解】解:设切点分别为D、E、F,连接OD、OE、OF,
∵⊙O为Rt△ABC的内切圆,
∴AE=AF、BD=BF、CD=CE,OD⊥BC,OE⊥AC,
∵∠C=90°,
∴四边形CDOE为正方形,
∴∠EOF+∠FOD=360°-90°=270°,
设⊙O的半径为x,则CD=CE=x,AE=AF=4-x,BD=BF=3-x,
∴4-x+3-x=5,
解得x=1,
∴S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE
=×3×4-×1×1
=-.
故答案为:-.
【点睛】本题考查了切线长定理,扇形的面积公式,熟记各图形的性质并准确识图是解题的关键.
2.(2022·湖北武汉·中考真题)如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
【答案】B
【分析】如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,据此求解即可.
【详解】解:如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,
∵,∠BAD=90°,
∴△EAD∽△EBC,∠B=90°,
∴,即,
∴,
∴EB=32cm,
∴,
设这个圆的圆心为O,与EB,BC,EC分别相切于F,G,H,
∴OF=OG=OH,
∵,
∴,
∴,
∴,
∴此圆的半径为8cm,
故选B.
【点睛】本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.
3.(2022·山东泰安·中考真题)如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】C
【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是△ACM的中位线即可解决问题.
【详解】解:延长ID到M,使DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,
∵AE=EC,
∴IE是△ACM的中位线,
∴IE=CM=4,故选:C.
【点睛】本题考查三角形的内心、三角形的外接圆、三角形的中位线定理、直角三角形的判定、勾股定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题.
同课章节目录
