2.2.2直线的两点式方程 课件(共31张PPT)
文档属性
| 名称 | 2.2.2直线的两点式方程 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 674.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 14:36:17 | ||
图片预览










文档简介
(共31张PPT)
2.2.2的两点式方程
复习引入
复习引入
直线方程名称 已知条件 直线方程 适用范围
点斜式
斜截式
复习引入
直线方程名称 已知条件 直线方程 适用范围
点斜式
斜截式
点和斜率
斜率, 在轴上的截距
斜率必须存在
斜率不存在时,
复习引入
已知直线经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2 ),因为两点确定一条直线,所以直线是唯一确定的.
复习引入
思考:直线上的任意一点P(x,y),它的坐标与点P1、P2的坐标之间具有唯一确定的关系,那这一关系是什么呢?
已知直线经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2 ),因为两点确定一条直线,所以直线是唯一确定的.
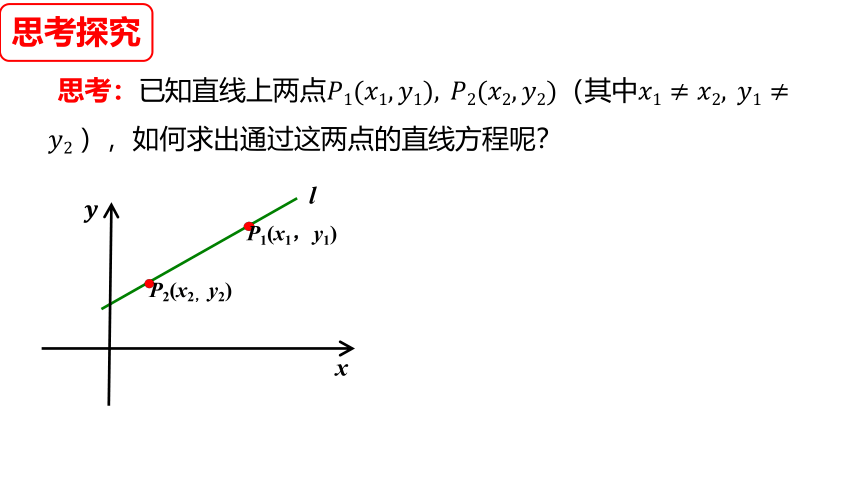
思考:已知直线上两点(其中),如何求出通过这两点的直线方程呢?
思考探究
x
l
P2(x2,y2)
P1(x1,y1)
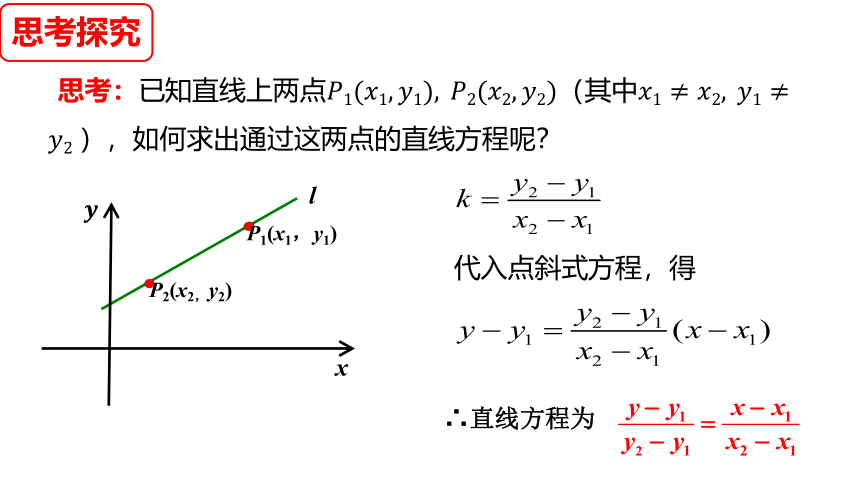
思考:已知直线上两点(其中),如何求出通过这两点的直线方程呢?
x
l
P2(x2,y2)
P1(x1,y1)
代入点斜式方程,得
∴直线方程为
思考探究
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
特点
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
特点
1.两边均是分式形式
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
3.两边的分母全为常数
4.分子,分母中的减数相同
2.左边全为,右边全为
特点
1.两边均是分式形式
新知讲解
直线的两点式方程:
(其中)
思考:是不是任何直线都有两点式方程呢?
不是!
新知讲解
直线的两点式方程:
(其中)
思考:是不是任何直线都有两点式方程呢?
不是!
当时,直线没有两点式程.
(因为时,两点式的分母为零,没有意义)
新知讲解
直线的两点式方程:
(其中)
注意:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
3.当 时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
3.当 时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
巩固训练
练习1.求经过下列两点的直线的两点式方程,再化成斜截式方程.
(1)
(2)
(3)
典例剖析
例1 如图,已知直线与轴的交点为,与轴的交点为,其中求直线的方程.
l
A(a,0)
B(0,b)
典例剖析
例1 如图,已知直线与轴的交点为,与轴的交点为,其中求直线的方程.
l
A(a,0)
B(0,b)
解: 将两点的坐标代入两点式,得:
即
所以直线的方程为:
新知讲解
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
直线在轴上的截距
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
直线在轴上的截距
直线的截距式方程:
思考:是不是任何直线都有截距式方程呢?
不能表示过原点或与坐标轴垂直的直线.
截距式适用于横、纵截距都存在且都不为0的直线.
巩固训练
练习2.
典例剖析
例2⑴过点并且在两个坐标轴上的截距相等的直线有几条 并求其方程.
(2) 过并且在两个坐标轴上的截距的绝对值相等的直线有几条 并求其方程.
典例剖析
例2⑴过点并且在两个坐标轴上的截距相等的直线有几条 并求其方程.
解: ⑴ 两条
所以直线方程为:
解得
把点(1,2)的坐标代入,得:
设直线的方程为:
①当直线不过原点时,
②当直线过原点时,直线方程为:
所以所求直线方程为:.
解:三条
所以直线方程为:或或.
①当直线的两截距相等过原点时,
②当直线的两截距相等不过原点时,
③当直线的两截距互为相反数时,
例2 (2) 过并且在两个坐标轴上的截距的绝对值相等的直线有几条 并求其方程.
典例剖析
巩固训练
练习3.根据下列条件求直线方程
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
课堂小结
名 称 方程
点斜式
斜截式
两点式
截距式
条 件
适用范围
直线方程的四种形式
课堂小结
名 称 方程
点和斜率
点斜式
斜截式
两点式
截距式
斜率, 在轴上的纵截距
在轴上的截距
和在轴上的截距
不垂直于轴的直线
不垂直于轴的直线
不垂直于轴、
轴的直线
不垂直于轴、轴,且不过原点的直线
条 件
适用范围
1.直线方程的四种形式
2.2.2的两点式方程
复习引入
复习引入
直线方程名称 已知条件 直线方程 适用范围
点斜式
斜截式
复习引入
直线方程名称 已知条件 直线方程 适用范围
点斜式
斜截式
点和斜率
斜率, 在轴上的截距
斜率必须存在
斜率不存在时,
复习引入
已知直线经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2 ),因为两点确定一条直线,所以直线是唯一确定的.
复习引入
思考:直线上的任意一点P(x,y),它的坐标与点P1、P2的坐标之间具有唯一确定的关系,那这一关系是什么呢?
已知直线经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2 ),因为两点确定一条直线,所以直线是唯一确定的.
思考:已知直线上两点(其中),如何求出通过这两点的直线方程呢?
思考探究
x
l
P2(x2,y2)
P1(x1,y1)
思考:已知直线上两点(其中),如何求出通过这两点的直线方程呢?
x
l
P2(x2,y2)
P1(x1,y1)
代入点斜式方程,得
∴直线方程为
思考探究
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
特点
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
特点
1.两边均是分式形式
新知讲解
直线的两点式方程:
经过两点(其中)的
直线方程为
我们把它叫做直线的两点式方程,简称两点式.
3.两边的分母全为常数
4.分子,分母中的减数相同
2.左边全为,右边全为
特点
1.两边均是分式形式
新知讲解
直线的两点式方程:
(其中)
思考:是不是任何直线都有两点式方程呢?
不是!
新知讲解
直线的两点式方程:
(其中)
思考:是不是任何直线都有两点式方程呢?
不是!
当时,直线没有两点式程.
(因为时,两点式的分母为零,没有意义)
新知讲解
直线的两点式方程:
(其中)
注意:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
3.当 时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
新知讲解
直线的两点式方程:
(其中)
注意:
2.当时直线与轴垂直,其方程为:
3.当 时直线与轴垂直,其方程为:
1.两点式不能表示平行于坐标轴或与坐标轴重合的直线.
巩固训练
练习1.求经过下列两点的直线的两点式方程,再化成斜截式方程.
(1)
(2)
(3)
典例剖析
例1 如图,已知直线与轴的交点为,与轴的交点为,其中求直线的方程.
l
A(a,0)
B(0,b)
典例剖析
例1 如图,已知直线与轴的交点为,与轴的交点为,其中求直线的方程.
l
A(a,0)
B(0,b)
解: 将两点的坐标代入两点式,得:
即
所以直线的方程为:
新知讲解
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
直线在轴上的截距
观察并思考:方程中的 各有何意义
新知讲解
直线在轴上的截距
直线在轴上的截距
直线的截距式方程:
思考:是不是任何直线都有截距式方程呢?
不能表示过原点或与坐标轴垂直的直线.
截距式适用于横、纵截距都存在且都不为0的直线.
巩固训练
练习2.
典例剖析
例2⑴过点并且在两个坐标轴上的截距相等的直线有几条 并求其方程.
(2) 过并且在两个坐标轴上的截距的绝对值相等的直线有几条 并求其方程.
典例剖析
例2⑴过点并且在两个坐标轴上的截距相等的直线有几条 并求其方程.
解: ⑴ 两条
所以直线方程为:
解得
把点(1,2)的坐标代入,得:
设直线的方程为:
①当直线不过原点时,
②当直线过原点时,直线方程为:
所以所求直线方程为:.
解:三条
所以直线方程为:或或.
①当直线的两截距相等过原点时,
②当直线的两截距相等不过原点时,
③当直线的两截距互为相反数时,
例2 (2) 过并且在两个坐标轴上的截距的绝对值相等的直线有几条 并求其方程.
典例剖析
巩固训练
练习3.根据下列条件求直线方程
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
课堂小结
名 称 方程
点斜式
斜截式
两点式
截距式
条 件
适用范围
直线方程的四种形式
课堂小结
名 称 方程
点和斜率
点斜式
斜截式
两点式
截距式
斜率, 在轴上的纵截距
在轴上的截距
和在轴上的截距
不垂直于轴的直线
不垂直于轴的直线
不垂直于轴、
轴的直线
不垂直于轴、轴,且不过原点的直线
条 件
适用范围
1.直线方程的四种形式
