数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究夹角问题 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究夹角问题 课件(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 16:47:28 | ||
图片预览


文档简介
(共19张PPT)
1.4.2用空间向量研究夹角问题
单位向量:
投影向量:
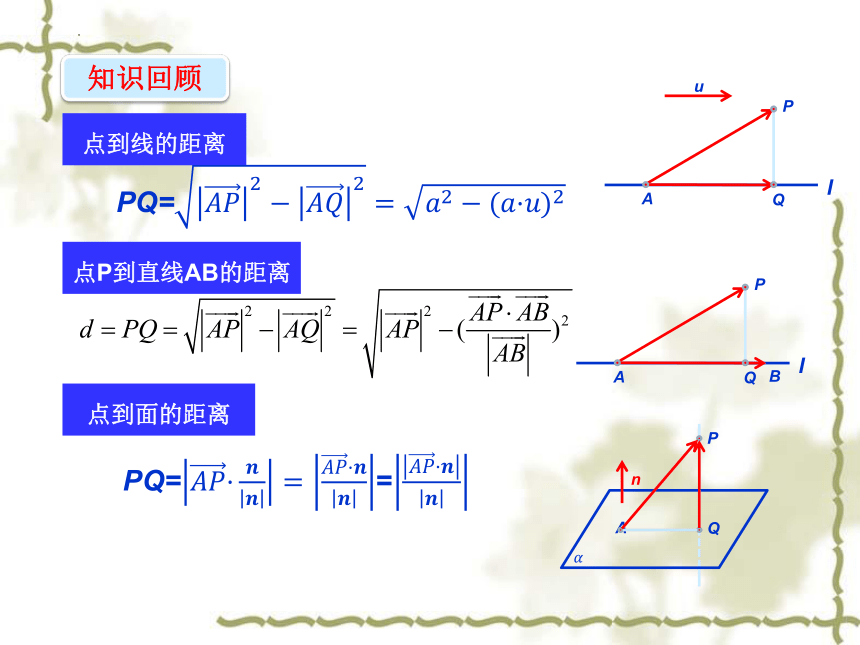
知识回顾
投影:
点到线的距离
点P到直线AB的距离
PQ=
l
A
Q
P
知识回顾
l
A
u
Q
P
B
点到面的距离
PQ==
n
P
A
Q
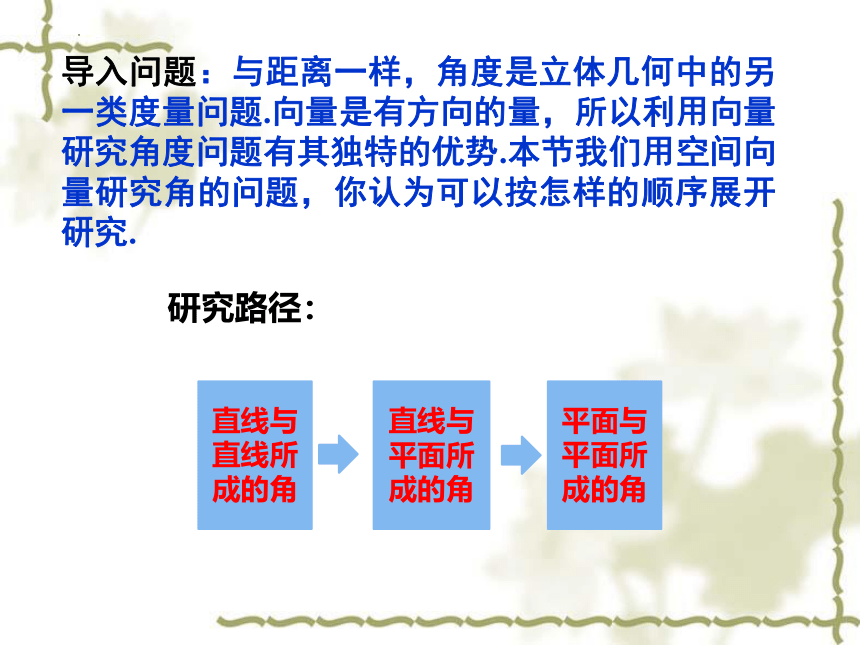
直线与直线所成的角
直线与平面所成的角
平面与平面所成的角
导入问题:与距离一样,角度是立体几何中的另一类度量问题.向量是有方向的量,所以利用向量研究角度问题有其独特的优势.本节我们用空间向量研究角的问题,你认为可以按怎样的顺序展开研究.
研究路径:
直线和夹角的余弦值
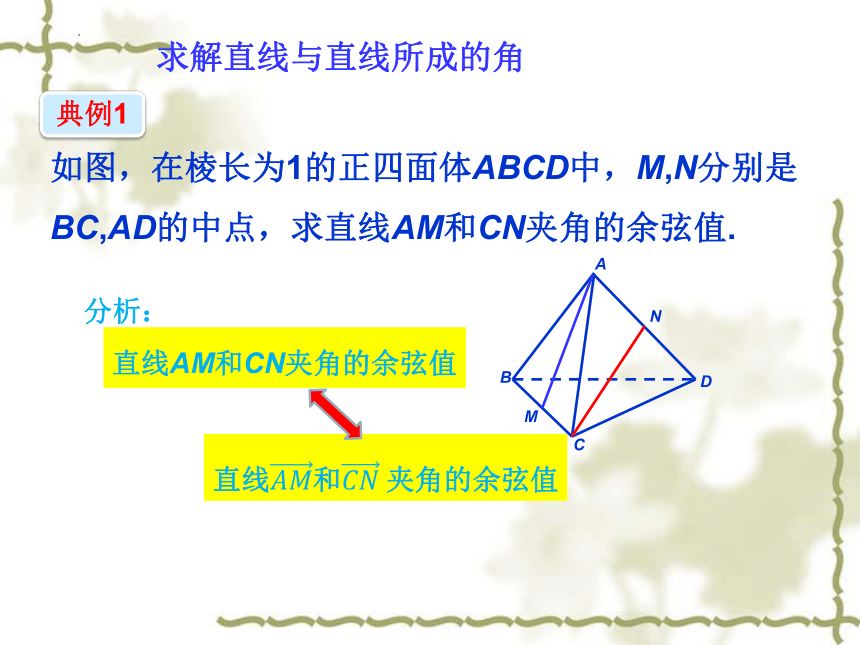
求解直线与直线所成的角
如图,在棱长为1的正四面体ABCD中,M,N分别是BC,AD的中点,求直线AM和CN夹角的余弦值.
A
B
C
D
N
M
分析:
直线AM和CN夹角的余弦值
典例1
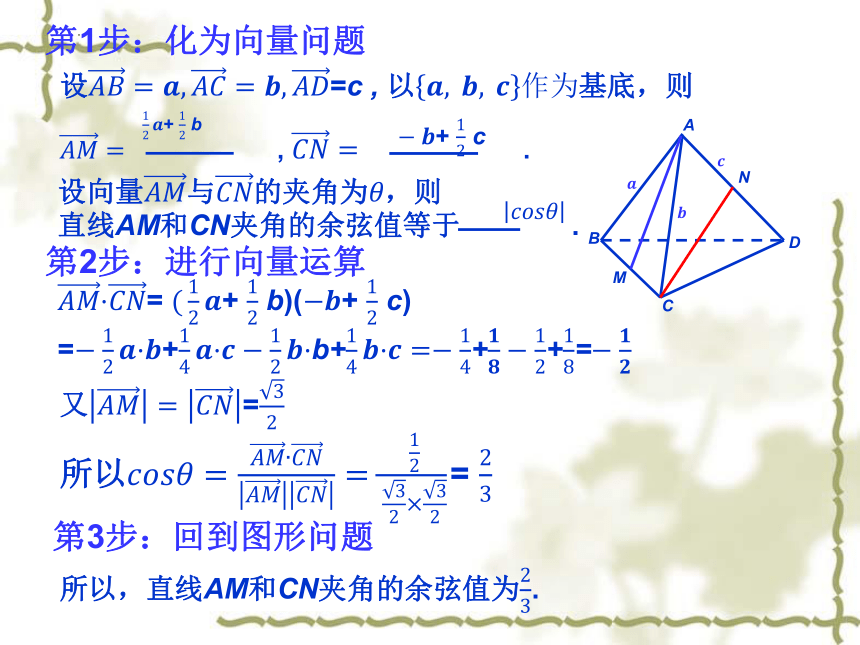
第1步:化为向量问题
第2步:进行向量运算
= + b)(+ c)
=+b+++=
A
B
C
D
N
M
又=
所以=
第3步:回到图形问题
所以,直线AM和CN夹角的余弦值为.
+ b
设=c , 以基底,则
, .
设向量与的夹角为,则
直线AM和CN夹角的余弦值等于 .
+ c
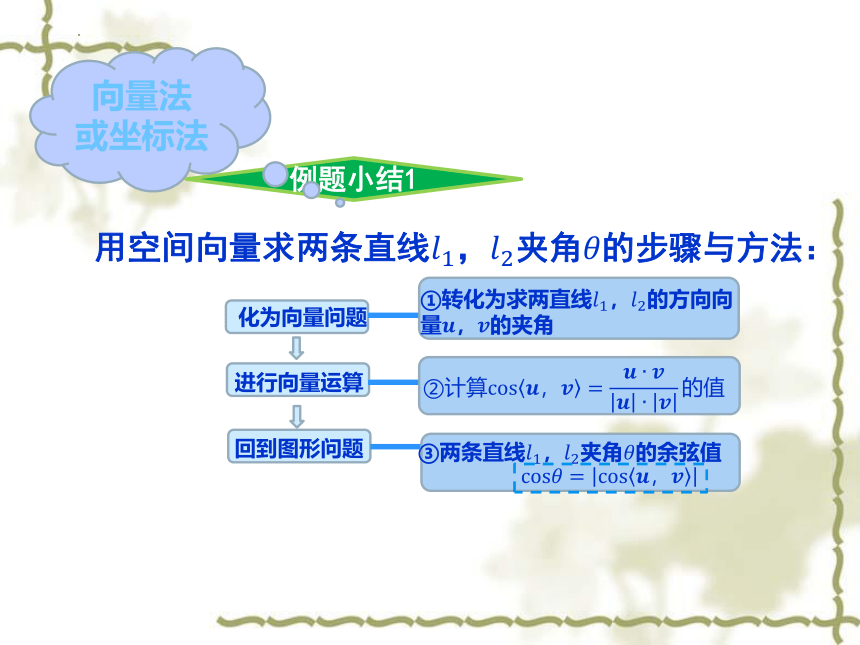
用空间向量求两条直线,夹角的步骤与方法:
例题小结1
化为向量问题
进行向量运算
回到图形问题
①转化为求两直线,的方向向量,的夹角
③两条直线,夹角的余弦值
向量法
或坐标法
解:过A作AO垂直于平面BCD,易知
分别以直线OC,OA,为x,z轴,
建立空间直角坐标系(如右图).
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
用向量方法解决几何问题的基本步骤:
几何问题 向量问题 向量运算 几何解释
归纳总结
问题2你能用向量方法求问题1中的直线AB
与平面BCD所成的角吗?
如何用空间向量求直线与平面所成的角?
追问:这个问题的已知条件是什么?
如何将几何问题转化成向量问题?
直线与平面所成的角,可以转化为
直线的方向向量与平面的法向量的夹角.
若直线AB的方向向量为u,平面的
法向量为n,直线与平面的夹角为,
则
s =
直线AB与平面BCD所成的角的正弦值
问题3:类比已有的直线、平面所成角的定义,你认为应如何合理定义两个平面所成的角?进一步地,如何求平面和平面的夹角?
如图,平面和平面相交,形成四个二面角,我们把这
四个二面角中不大于 的二面角称为和的夹角.
平面与平面所成的角,可以转化为法向量与法向量的夹角.
若平面的法向量分别为n1n2,
cos =
则平面与平面的夹角即为向量n1n2的夹角或其补角.
设平面与平面的夹角为,则
平面与平面的夹角与二面角的区别和联系:
二面角的大小是指其两个半平面的张开程度,可以用其平面角的大小来
定义,它的取值范围是:0
而平面和平面的夹角是指平面和平面相交,形成的四个二面角中
不大于 的二面角.
解:①化为向量问题
②进行向量运算
③回到图形问题
用空间向量解决立体几何问题的“三步曲”:
小结
①建立空间立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体解决问题转化为向量问题;
(化为向量问题)
②通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;(进行向量运算)
③把向量运算的结果“翻译”成相应的几何结论.(回到图形问题)
直线与直线的夹角
直线与平面的夹角
cos =
s =
平面与平面的夹角
cos =
l1
l2
u
v
n
B
A
C
u
n1
n2
(1)这节课主要学习了哪些内容?
(2)研究这些内容主要用了什么方法?
(3)用向量方法解决立体几何问题的一般步骤是什么?
4.归纳小结
教科书习题1.4第9,10题.
5.布置作业
教科书练习第1,2,3,4题.
目标检测设计
谢谢
再见
1.4.2用空间向量研究夹角问题
单位向量:
投影向量:
知识回顾
投影:
点到线的距离
点P到直线AB的距离
PQ=
l
A
Q
P
知识回顾
l
A
u
Q
P
B
点到面的距离
PQ==
n
P
A
Q
直线与直线所成的角
直线与平面所成的角
平面与平面所成的角
导入问题:与距离一样,角度是立体几何中的另一类度量问题.向量是有方向的量,所以利用向量研究角度问题有其独特的优势.本节我们用空间向量研究角的问题,你认为可以按怎样的顺序展开研究.
研究路径:
直线和夹角的余弦值
求解直线与直线所成的角
如图,在棱长为1的正四面体ABCD中,M,N分别是BC,AD的中点,求直线AM和CN夹角的余弦值.
A
B
C
D
N
M
分析:
直线AM和CN夹角的余弦值
典例1
第1步:化为向量问题
第2步:进行向量运算
= + b)(+ c)
=+b+++=
A
B
C
D
N
M
又=
所以=
第3步:回到图形问题
所以,直线AM和CN夹角的余弦值为.
+ b
设=c , 以基底,则
, .
设向量与的夹角为,则
直线AM和CN夹角的余弦值等于 .
+ c
用空间向量求两条直线,夹角的步骤与方法:
例题小结1
化为向量问题
进行向量运算
回到图形问题
①转化为求两直线,的方向向量,的夹角
③两条直线,夹角的余弦值
向量法
或坐标法
解:过A作AO垂直于平面BCD,易知
分别以直线OC,OA,为x,z轴,
建立空间直角坐标系(如右图).
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
用向量方法解决几何问题的基本步骤:
几何问题 向量问题 向量运算 几何解释
归纳总结
问题2你能用向量方法求问题1中的直线AB
与平面BCD所成的角吗?
如何用空间向量求直线与平面所成的角?
追问:这个问题的已知条件是什么?
如何将几何问题转化成向量问题?
直线与平面所成的角,可以转化为
直线的方向向量与平面的法向量的夹角.
若直线AB的方向向量为u,平面的
法向量为n,直线与平面的夹角为,
则
s =
直线AB与平面BCD所成的角的正弦值
问题3:类比已有的直线、平面所成角的定义,你认为应如何合理定义两个平面所成的角?进一步地,如何求平面和平面的夹角?
如图,平面和平面相交,形成四个二面角,我们把这
四个二面角中不大于 的二面角称为和的夹角.
平面与平面所成的角,可以转化为法向量与法向量的夹角.
若平面的法向量分别为n1n2,
cos =
则平面与平面的夹角即为向量n1n2的夹角或其补角.
设平面与平面的夹角为,则
平面与平面的夹角与二面角的区别和联系:
二面角的大小是指其两个半平面的张开程度,可以用其平面角的大小来
定义,它的取值范围是:0
而平面和平面的夹角是指平面和平面相交,形成的四个二面角中
不大于 的二面角.
解:①化为向量问题
②进行向量运算
③回到图形问题
用空间向量解决立体几何问题的“三步曲”:
小结
①建立空间立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体解决问题转化为向量问题;
(化为向量问题)
②通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;(进行向量运算)
③把向量运算的结果“翻译”成相应的几何结论.(回到图形问题)
直线与直线的夹角
直线与平面的夹角
cos =
s =
平面与平面的夹角
cos =
l1
l2
u
v
n
B
A
C
u
n1
n2
(1)这节课主要学习了哪些内容?
(2)研究这些内容主要用了什么方法?
(3)用向量方法解决立体几何问题的一般步骤是什么?
4.归纳小结
教科书习题1.4第9,10题.
5.布置作业
教科书练习第1,2,3,4题.
目标检测设计
谢谢
再见
