6.2.1排列+6.2.2排列数 课件(共21张PPT)
文档属性
| 名称 | 6.2.1排列+6.2.2排列数 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 16:55:53 | ||
图片预览







文档简介
(共21张PPT)
6.2.1 排列6.2.2排列数
人教A版 高中数学选择性必修三第六章
高 二 年 级
情景引入
1.理解排列的概念,能正确写出一些简单问题的所有排列.
2.能够用列举法,树状图、排列数公式求排列数.
1.通过学习排列的概念,体现了数学抽象的素养.
2.能够用列举法,树状图求排列方法种数,培养数学运算的素养.
素养要求
课标要求
教学目标
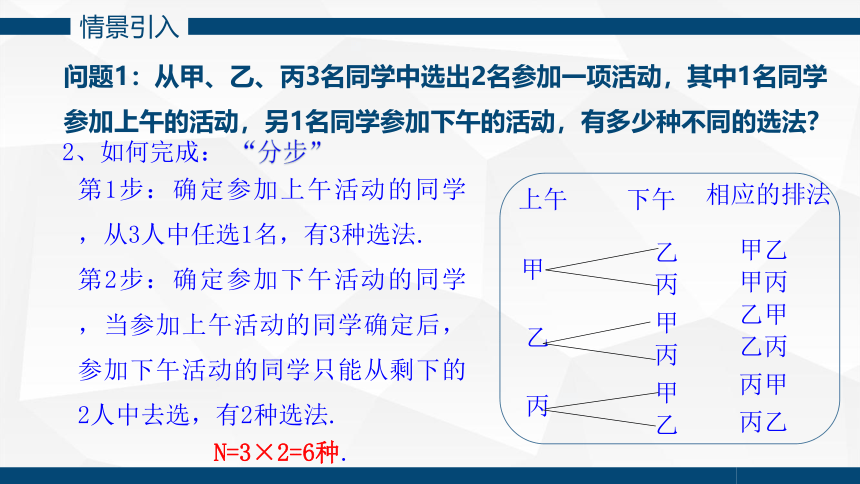
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
情景引入
2.如何完成:
1.“要完成的一件事”:
选1名同学参加上午的活动,另1名同学参加下午的活动
“分步”
分析:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
情景引入
2、如何完成:
第1步:确定参加上午活动的同学,从3人中任选1名,有3种选法.
第2步:确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种选法.
N=3×2=6种.
“分步”
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
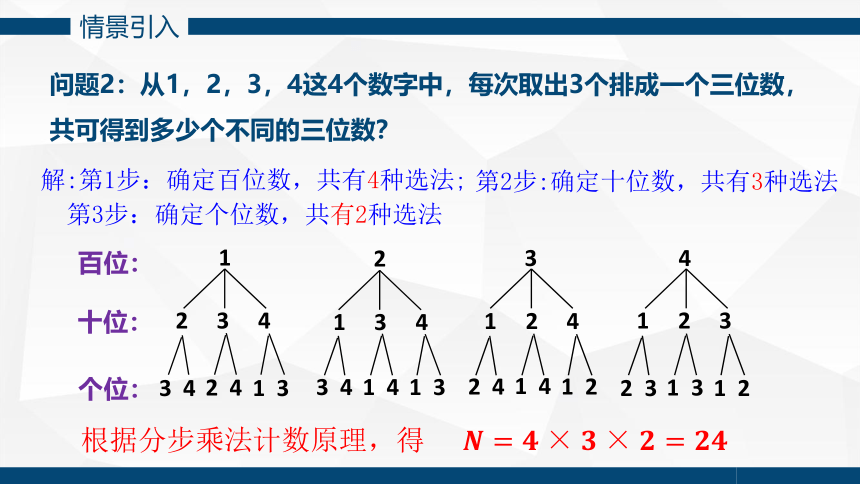
问题2:从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
情景引入
解:第1步:确定百位数,共有4种选法;
第2步:确定十位数,共有3种选法
第3步:确定个位数,共有2种选法
百位:
十位:
个位:
1
2
3
4
2 3 4
1 3 4
1 2 4
1 2 3
3 4
2 4
1 3
3 4
1 4
1 3
2 4
1 4
1 2
2 3
1 3
1 2
根据
问题3:如将问题1、问题2 取出的对象称为元素,那么他们的共同
特点是什么?能否推广到一般情形?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
情景引入
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
两个排列相同的充要条件是:
例如:在问题1中,“甲乙”与“甲丙”是否为同一排列( );
“甲乙”与“乙甲”是否为同一排列( ).
两个排列的元素完全相同,且排列顺序也相同.
新知学习
注:(1) 元素的互异性;
(2) 元素的有序性
(3)是排法,不是数
改变元素位置,结果是否变化
(1)从高二3班全体同学中选5人组成课外数学学习小组;
(2)从高二3班全体同学中选5人分别参加运动会的5个不同的运动项目;
(3)从1,2,3三个数中取2个数相乘,求积的个数;
(4)从1,2,3三个数中取2个数作商,求商的个数.
(5)景曹分校3个校门,从1个校门入校,1个校门出校,出入方式多少种
(6)平面上有3个不共线的点,这三个点可确定多少条直线?多少射线?
例1 判断下列问题是否为排列问题.
例题讲解
√
√
×
×
√
×
√
例2 (1)学校食堂的一个窗户共卖5种菜,甲乙丙3名同学每人从中选一种,共有多少种不同的选法?
(2)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
例题讲解
解:(1)第1步:确定甲同学的菜,共有5种选法;
第2步:确定乙同学的菜,共有5种选法;
第3步:确定丙同学的菜,共有5种选法;
根据分布乘法计数原理 共N=5*5*5=125
不是
是
例2 (1)学校食堂的一个窗户共卖5种菜,甲乙丙3名同学每人从中选一种,共有多少种不同的选法?
(2)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
例题讲解
解:(2)第1步:确定甲同学的菜,共有5种选法;
第2步:确定乙同学的菜,共有4种选法;
第3步:确定丙同学的菜,共有3种选法;
根据分布乘法计数原理 共N=5*4*3=60
排列数的定义:
从个不同的元素中取出个元素的所有不同排列的个数,叫做从个不同的元素中取出个元素的排列数,用符号表示.
从3个不同元素中取出2个元素的排列数,表示为.
从4个不同元素中取出3个元素的排列数,表示为.
=3×2=6
=4×3×2=24
新知学习
第1位
第2位
1. :假定有排好顺序的2个空位
. . .
第1位
第位
第2位
第3位
2. 假定有排好顺序的个空位
思考:,,是多少?
种
种
种
种
种
种
?
同理:
新知学习
1. 排列数公式:
正整数1到的连乘积,叫做的阶乘,用表示,即
2. 全排列的定义:
规定:
把个不同元素全部取出的一个排列,叫做 个元素的一个全排列.这时,
新知学习
排列数公式
新知学习
例3 计算:
解:
例题讲解
例4
例题讲解
3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
(2) 全体站成一排,甲、乙均不在两端;
(4) 全体站成一排,男生站一起;
(3) 全体站成一排,甲不在最左端;
例5 链接高考
例题讲解
2020全国卷II
4名同学到3个小区参加垃圾分类活动,每名同学只能去1个小区,每个小区至少1名同学,则不同的安排有( )种
分析:第一步选出2名同学,作为1个整体;第二步:将这3组同学分配至3个小区;
变式
现有5人排成1排照相,甲乙相邻,则不同的排法( ).
例题讲解
2020全国卷II
4名同学到3个小区参加垃圾分类活动,每名同学只能去1个小区,每个小区至少1名同学,则不同的安排有( )种
分析:第一步选出2名同学,作为1个整体;第二步:将这3组同学分配至3个小区;
解:第一步选出2名同学,共6种;第二步:
例5 链接高考
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
1. 排列的定义:
2. 排列问题的判断方法:
(1) 元素的互异性;(2) 元素的有序性
归纳总结
3. 排列数定义
一般地,从个不同元素中取出个元素所有不同排列的个数,称为排列数.
4. 排列数公式
全 品 导 学 案 p71--p75
课后作业
6.2.1 排列6.2.2排列数
人教A版 高中数学选择性必修三第六章
高 二 年 级
情景引入
1.理解排列的概念,能正确写出一些简单问题的所有排列.
2.能够用列举法,树状图、排列数公式求排列数.
1.通过学习排列的概念,体现了数学抽象的素养.
2.能够用列举法,树状图求排列方法种数,培养数学运算的素养.
素养要求
课标要求
教学目标
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
情景引入
2.如何完成:
1.“要完成的一件事”:
选1名同学参加上午的活动,另1名同学参加下午的活动
“分步”
分析:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
情景引入
2、如何完成:
第1步:确定参加上午活动的同学,从3人中任选1名,有3种选法.
第2步:确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种选法.
N=3×2=6种.
“分步”
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
问题2:从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
情景引入
解:第1步:确定百位数,共有4种选法;
第2步:确定十位数,共有3种选法
第3步:确定个位数,共有2种选法
百位:
十位:
个位:
1
2
3
4
2 3 4
1 3 4
1 2 4
1 2 3
3 4
2 4
1 3
3 4
1 4
1 3
2 4
1 4
1 2
2 3
1 3
1 2
根据
问题3:如将问题1、问题2 取出的对象称为元素,那么他们的共同
特点是什么?能否推广到一般情形?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
情景引入
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
两个排列相同的充要条件是:
例如:在问题1中,“甲乙”与“甲丙”是否为同一排列( );
“甲乙”与“乙甲”是否为同一排列( ).
两个排列的元素完全相同,且排列顺序也相同.
新知学习
注:(1) 元素的互异性;
(2) 元素的有序性
(3)是排法,不是数
改变元素位置,结果是否变化
(1)从高二3班全体同学中选5人组成课外数学学习小组;
(2)从高二3班全体同学中选5人分别参加运动会的5个不同的运动项目;
(3)从1,2,3三个数中取2个数相乘,求积的个数;
(4)从1,2,3三个数中取2个数作商,求商的个数.
(5)景曹分校3个校门,从1个校门入校,1个校门出校,出入方式多少种
(6)平面上有3个不共线的点,这三个点可确定多少条直线?多少射线?
例1 判断下列问题是否为排列问题.
例题讲解
√
√
×
×
√
×
√
例2 (1)学校食堂的一个窗户共卖5种菜,甲乙丙3名同学每人从中选一种,共有多少种不同的选法?
(2)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
例题讲解
解:(1)第1步:确定甲同学的菜,共有5种选法;
第2步:确定乙同学的菜,共有5种选法;
第3步:确定丙同学的菜,共有5种选法;
根据分布乘法计数原理 共N=5*5*5=125
不是
是
例2 (1)学校食堂的一个窗户共卖5种菜,甲乙丙3名同学每人从中选一种,共有多少种不同的选法?
(2)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
例题讲解
解:(2)第1步:确定甲同学的菜,共有5种选法;
第2步:确定乙同学的菜,共有4种选法;
第3步:确定丙同学的菜,共有3种选法;
根据分布乘法计数原理 共N=5*4*3=60
排列数的定义:
从个不同的元素中取出个元素的所有不同排列的个数,叫做从个不同的元素中取出个元素的排列数,用符号表示.
从3个不同元素中取出2个元素的排列数,表示为.
从4个不同元素中取出3个元素的排列数,表示为.
=3×2=6
=4×3×2=24
新知学习
第1位
第2位
1. :假定有排好顺序的2个空位
. . .
第1位
第位
第2位
第3位
2. 假定有排好顺序的个空位
思考:,,是多少?
种
种
种
种
种
种
?
同理:
新知学习
1. 排列数公式:
正整数1到的连乘积,叫做的阶乘,用表示,即
2. 全排列的定义:
规定:
把个不同元素全部取出的一个排列,叫做 个元素的一个全排列.这时,
新知学习
排列数公式
新知学习
例3 计算:
解:
例题讲解
例4
例题讲解
3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
(2) 全体站成一排,甲、乙均不在两端;
(4) 全体站成一排,男生站一起;
(3) 全体站成一排,甲不在最左端;
例5 链接高考
例题讲解
2020全国卷II
4名同学到3个小区参加垃圾分类活动,每名同学只能去1个小区,每个小区至少1名同学,则不同的安排有( )种
分析:第一步选出2名同学,作为1个整体;第二步:将这3组同学分配至3个小区;
变式
现有5人排成1排照相,甲乙相邻,则不同的排法( ).
例题讲解
2020全国卷II
4名同学到3个小区参加垃圾分类活动,每名同学只能去1个小区,每个小区至少1名同学,则不同的安排有( )种
分析:第一步选出2名同学,作为1个整体;第二步:将这3组同学分配至3个小区;
解:第一步选出2名同学,共6种;第二步:
例5 链接高考
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
1. 排列的定义:
2. 排列问题的判断方法:
(1) 元素的互异性;(2) 元素的有序性
归纳总结
3. 排列数定义
一般地,从个不同元素中取出个元素所有不同排列的个数,称为排列数.
4. 排列数公式
全 品 导 学 案 p71--p75
课后作业
