人教版数学九年级下册27.2.1相似三角形的判定 学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册27.2.1相似三角形的判定 学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 20:54:38 | ||
图片预览

文档简介
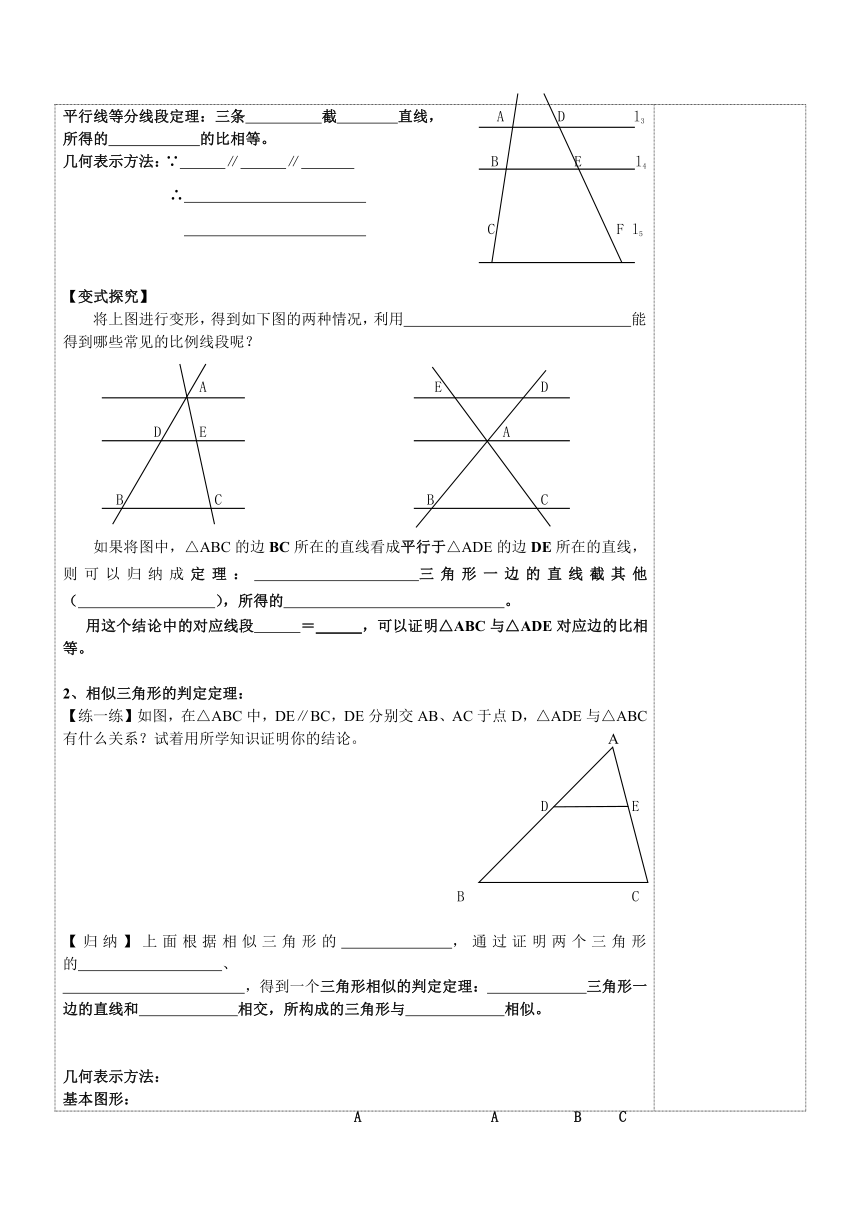
课题:相似三角行的判定(1)学习目标:理解相似三角形的概念及其表示方法2、理解并会应用平行线分线段成比例定理3、理解并会熟练的应用相似三角形的判定定理(平行线法)学习过程:一、预习准备根据“相似图形”的定义和性质,我们可以得到相似三角形的定义和性质。1、相似三角形的定义:如果两个三角形的对应边 ,对应角 ,那么这两个三角形相似。其中 叫做它们的相似比。△A1B1C1与△ABC相似,记作: 。2、相似三角形的性质:∵△ABC ∽ △A1B1C1∴∠A ∠A1 ∠B ∠B1 ∠C ∠C1 = = 3、相似比:将△ABC与△A1B1C1的相似比记为,△A1B1C1与△ABC的相似比记为,则与的关系是 ,当且仅当 时,== ,因此 是三角形相似的特例。 A【练一练】(1)如图,∵△ABC∽△ADE, D ∴∠ABC=∠ADE ∠ =∠ = = E(2)如果△ABC∽△A1B1C1,相似比为(≠1), C B则与的值相等的是( )A. ∠A∶∠A1 B. A1B1∶AB C. ∠B∶∠B1 D. BC∶B1C1(3)三角形三边之比为3∶5∶7,与它相似的三角形最长边是21,另两边之和是 。二、探索新知1、平行线分线段成比例定理及其推论:如图,任意画两条直线,再画三条与相交的平行线,分别度量在上截得的两条线段AB、BC和在上截得的两条线段DE、EF的长度,与相等吗?任意平移,再度量这些线段的长度,刚才所得到的结论仍然成立吗?如果成立,请你用自己的话将这个规律总结出来。 l1 l2平行线等分线段定理:三条 截 直线, A D l3所得的 的比相等。几何表示方法:∵ ∥ ∥ B E l4 ∴ C F l5【变式探究】将上图进行变形,得到如下图的两种情况,利用 能得到哪些常见的比例线段呢? A E D D E A B C B C 如果将图中,△ABC的边BC所在的直线看成平行于△ADE的边DE所在的直线,则可以归纳成定理: 三角形一边的直线截其他 ( ),所得的 。 用这个结论中的对应线段 = ,可以证明△ABC与△ADE对应边的比相等。2、相似三角形的判定定理:【练一练】如图,在△ABC中,DE∥BC,DE分别交AB、AC于点D,△ADE与△ABC有什么关系?试着用所学知识证明你的结论。 A D E B C【归纳】上面根据相似三角形的 ,通过证明两个三角形的 、 ,得到一个三角形相似的判定定理: 三角形一边的直线和 相交,所构成的三角形与 相似。几何表示方法: 基本图形:∵ ∥ ∴△ ∽△ B C D E D E B C E D例1 如图,DE∥BC,EF∥AB,(1)图中相似形三角形有 对,分别是 ;(2)如果AD=5,DB=3,FC=2,则△ADE与△ABC的相似比是 ;(3)求BF的长。 A D E B F C【练一练】如图,D、E分别是△ABC两条边的中点,EG=2GC,DG、BC的延长线交予点F,已知CF的长为1,求BC的长。 A D E G B C F 例2 如图,已知□ABCD中,E为AB延长线上的一点,AB=3BE,DE与BC相交于点F,请你找出图中各对相似三角形,并求出相应的相似比。 E C F B D A【练一练】在□ABCD中,E在BC的延长线上,AE交BD于F,交CD于G,(1)图中相似三角形有 对,分别是 ;(2)若DG∶CG=4∶3,求AF∶FE的值。 A D F G B C E例3 如图,在△ABC中,∠C=90°,AC=3,D为BC边上一点,过D点作DE⊥BC交AB于E,若DE=1,BD=2,求DC的长。 A E C D B例4 如图,在△APM的边AP上任取两点B和C,过点B作AM的平行线交PM于N,过点N作MC的平行线交AP于点D,求证:PA∶PB=PC∶PD。 A B C D P例5 如图,过△ABC的顶点C作任一直线,与边AB及中线AD分别交于点E和F,求证:AF∶FD=2AE∶EB。 A F B D C延伸:1、若D、E分别是边BC、AB的中点,AD、CE相交于点F,求证: ; 2、如图,已知△ABC中,延长BC到点D,使CD=BC,取AB的中点F,连接FD交AC于点E,(1)求的值; (2)若AB=,FB=EC,求AC的长。 F E 二次备课
A
C
B
A
A
M
N
E
A
D
C
B
A
C
B
A
A
M
N
E
A
D
C
B
