新课标北师大版四下数学好玩第1课时《密铺》课件(37张PPT)
文档属性
| 名称 | 新课标北师大版四下数学好玩第1课时《密铺》课件(37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 08:56:26 | ||
图片预览










文档简介
(共37张PPT)
密铺
北师大版四年级下册
教学目标
1.学习目标描述:借助生活中常见的密铺现象,初步理解图形的密铺;通过拼摆各种图形,探索并了解能够进行密铺平面图形的特点。
2.学习内容分析:这是一节数学实践活动,通过学生的动手操作感知密铺图形的形状,理解密铺的特征。了解图形密铺在生活中的应用,增强应用数学的意识通过活动,可以使学生进一步了解有关平面图形
教学目标
的特征,感受数学学习的乐趣,体会数学知识与方法在生活中的广泛应用。
3.学科核心素养分析:能进行简单的密铺设计,积累相关活动经验,培养初步的空间观念,提高解决问题的能力。结合密铺活动感受数学在生活中的广泛应用,发展学生对数学学习的兴趣;结合自我评价发展学生反思能力。
新知导入
浅颜色的是个骑士,深颜色的也是个骑士。
这幅图的奇妙之处就在于大小相同,左右相对的骑士刚刚好紧密地拼接在了一块儿!
新知导入
在装修时经常要在地面或墙面铺上砖,下面是几种瓷砖的铺法。
思考:
请仔细观家这些图案是由哪些围形铺成的?它们有什么共同的特点
新知导入
图形之间没有空隙,也不重叠,是密铺。
什么图形可以密铺?
为什么有的图形可以密铺呢?
新知讲解
学校要在教室的地面铺地砖,现在有如下形状的地砖。
猜一猜哪些可以密铺,哪些不可以密铺。
活动任务
三角形能不能密铺?四边形可不可以?
新知讲解
(1)解决这个问题需要哪些主要步骤?
(2)你想采取怎样的方式解决问题?(独立完成/小组合作),如果是小组合作,怎样进行分工?
(3)把主要步骤,分工写下来。
设计方案
新知讲解
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
活动要求:
1.小组合作,每人选择一种图形铺一铺。
2.想一想铺的过程中要注意什么。
3.将铺的结果在小组里交流。
新知讲解
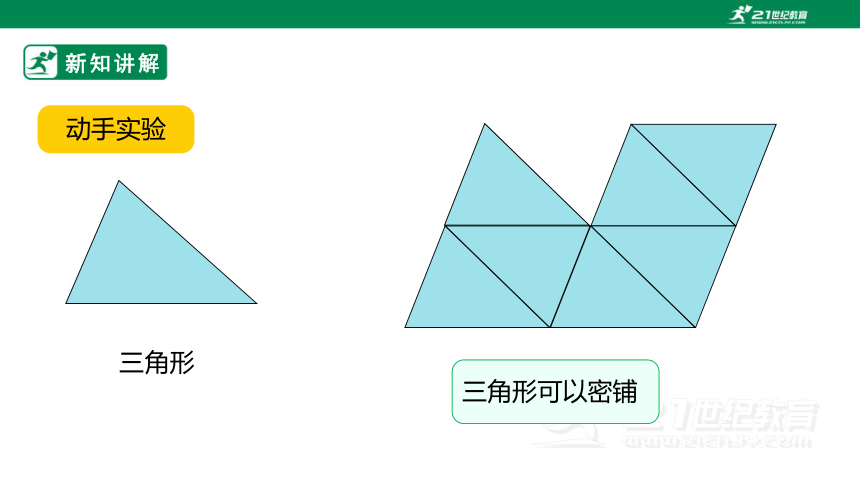
三角形可以密铺
三角形
动手实验
新知讲解
平行四边形可以密铺
平行四边形
新知讲解
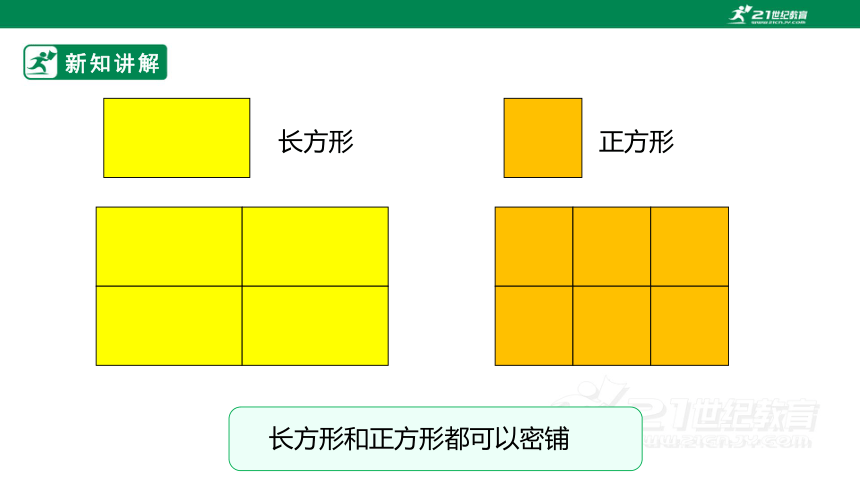
长方形和正方形都可以密铺
长方形 正方形
新知讲解
梯形可以密铺
梯形
新知讲解
任意四边形也可以密铺
任意四边形
新知讲解
三角形和四边形都可以密铺,为什么可以呢?
图形之间没有空隙,也不重叠。
新知讲解
请按照下面的方法试一试,将相同图形的角按序号标好,密铺后你有什么发现?
交流反思
提示:用三角形或四边形密铺的图案中,每个拼接点处有几个角?它们与这个图形的内角有什么关系
新知讲解
在三角形拼接的图案中,每个拼接点处有6个角,分别等于一个三角形的各内角。它们的和为360度,是三角形的内角和180度的2倍。
新知讲解
在四边形的拼接图案中,每一个拼接点处应有4个角,分别等于一个四边形的4个内角,它们的和等于四边形的内角和360度。
新知讲解
符合密铺要求的多边形应该具备什么样的条件?
只用一种多边形进行密铺,就必须使拼凑在每一个顶点处各角度数之和为360°。
新知讲解
在上面的活动中,你有什么收获?还有哪些想要进一步研究的问题呢?
我发现密铺与图形的角有关……
所有平面图形都能密铺吗?
新知讲解
用刚才的方法再试一试。
圆
圆不能密铺
新知讲解
不是所有的平面图形都可以密铺,用正五边形和正六边形试试。
剩下的角比正五边形的角小,放不进去。
正五边形不能密铺。
新知讲解
不是所有的平面图形都可以密铺,用正五边形和正六边形试试。
正六边形能密铺。
新知讲解
正五边形不能密铺,可以借助其他图形。
用同一种平面图形如果不能密铺,可以用两种或两种以上平面图形进行密铺。
新知讲解
看一看下面的密铺图案,想一想它们是如何形成的。
由四边形密铺
由六边形密铺
新知讲解
看一看下面的密铺图案,想一想它们是如何形成的。
由图案密铺
新知讲解
自我评价
在这次活动中,我的表现是(请把每项后面的 涂上颜色,涂满5个为做得最好的):
能设计合理的解决问题的方案。
能够裁剪出所需的图形尝试密铺活动。
能把密铺活动与学过的图形知识相联系。
能与同伴合作交流。
能联系到生活中的密铺现象。
课堂练习
下面哪些图形可以密铺?给可以密铺的图形打“√”。
( ) ( ) ( )
( ) ( ) ( )
√
√
√
√
课堂练习
下面三幅图哪幅是密铺 给是密铺的图形打“√”。
( ) ( ) ( )
√
√
课堂练习
仔细观察下面的图,它们是由哪些基本图形密铺形成的?在下面画出这个基本图形。
课堂练习
拓展应用:(1)算一算,并说说为什么正五边形不能密铺?
正五边形内角和:3×180°=540°
每个角的度数:540°÷5=108°
108°×3=324° 324°<360°
所以正五边形不能密铺。
课堂练习
拓展应用:(2)算一算,并说说为什么正六边形能密铺?
正六边形内角和:4×180°=720°
每个角的度数:720°÷6=120°
120°×3=360°
所以正六边形能密铺。
课堂总结
通过今天的学习,你有哪些收获?
我知道图形之间没有空隙,也不重叠,是密铺。
我还会判断哪些图形可以密铺。
板书设计
密 铺
无空隙 不重叠
三角形、四边形、正六边形可以密铺
圆、正五边形不能密铺
作业布置
利用一种图形或几种图形设计一幅密铺图案。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
密铺
北师大版四年级下册
教学目标
1.学习目标描述:借助生活中常见的密铺现象,初步理解图形的密铺;通过拼摆各种图形,探索并了解能够进行密铺平面图形的特点。
2.学习内容分析:这是一节数学实践活动,通过学生的动手操作感知密铺图形的形状,理解密铺的特征。了解图形密铺在生活中的应用,增强应用数学的意识通过活动,可以使学生进一步了解有关平面图形
教学目标
的特征,感受数学学习的乐趣,体会数学知识与方法在生活中的广泛应用。
3.学科核心素养分析:能进行简单的密铺设计,积累相关活动经验,培养初步的空间观念,提高解决问题的能力。结合密铺活动感受数学在生活中的广泛应用,发展学生对数学学习的兴趣;结合自我评价发展学生反思能力。
新知导入
浅颜色的是个骑士,深颜色的也是个骑士。
这幅图的奇妙之处就在于大小相同,左右相对的骑士刚刚好紧密地拼接在了一块儿!
新知导入
在装修时经常要在地面或墙面铺上砖,下面是几种瓷砖的铺法。
思考:
请仔细观家这些图案是由哪些围形铺成的?它们有什么共同的特点
新知导入
图形之间没有空隙,也不重叠,是密铺。
什么图形可以密铺?
为什么有的图形可以密铺呢?
新知讲解
学校要在教室的地面铺地砖,现在有如下形状的地砖。
猜一猜哪些可以密铺,哪些不可以密铺。
活动任务
三角形能不能密铺?四边形可不可以?
新知讲解
(1)解决这个问题需要哪些主要步骤?
(2)你想采取怎样的方式解决问题?(独立完成/小组合作),如果是小组合作,怎样进行分工?
(3)把主要步骤,分工写下来。
设计方案
新知讲解
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
活动要求:
1.小组合作,每人选择一种图形铺一铺。
2.想一想铺的过程中要注意什么。
3.将铺的结果在小组里交流。
新知讲解
三角形可以密铺
三角形
动手实验
新知讲解
平行四边形可以密铺
平行四边形
新知讲解
长方形和正方形都可以密铺
长方形 正方形
新知讲解
梯形可以密铺
梯形
新知讲解
任意四边形也可以密铺
任意四边形
新知讲解
三角形和四边形都可以密铺,为什么可以呢?
图形之间没有空隙,也不重叠。
新知讲解
请按照下面的方法试一试,将相同图形的角按序号标好,密铺后你有什么发现?
交流反思
提示:用三角形或四边形密铺的图案中,每个拼接点处有几个角?它们与这个图形的内角有什么关系
新知讲解
在三角形拼接的图案中,每个拼接点处有6个角,分别等于一个三角形的各内角。它们的和为360度,是三角形的内角和180度的2倍。
新知讲解
在四边形的拼接图案中,每一个拼接点处应有4个角,分别等于一个四边形的4个内角,它们的和等于四边形的内角和360度。
新知讲解
符合密铺要求的多边形应该具备什么样的条件?
只用一种多边形进行密铺,就必须使拼凑在每一个顶点处各角度数之和为360°。
新知讲解
在上面的活动中,你有什么收获?还有哪些想要进一步研究的问题呢?
我发现密铺与图形的角有关……
所有平面图形都能密铺吗?
新知讲解
用刚才的方法再试一试。
圆
圆不能密铺
新知讲解
不是所有的平面图形都可以密铺,用正五边形和正六边形试试。
剩下的角比正五边形的角小,放不进去。
正五边形不能密铺。
新知讲解
不是所有的平面图形都可以密铺,用正五边形和正六边形试试。
正六边形能密铺。
新知讲解
正五边形不能密铺,可以借助其他图形。
用同一种平面图形如果不能密铺,可以用两种或两种以上平面图形进行密铺。
新知讲解
看一看下面的密铺图案,想一想它们是如何形成的。
由四边形密铺
由六边形密铺
新知讲解
看一看下面的密铺图案,想一想它们是如何形成的。
由图案密铺
新知讲解
自我评价
在这次活动中,我的表现是(请把每项后面的 涂上颜色,涂满5个为做得最好的):
能设计合理的解决问题的方案。
能够裁剪出所需的图形尝试密铺活动。
能把密铺活动与学过的图形知识相联系。
能与同伴合作交流。
能联系到生活中的密铺现象。
课堂练习
下面哪些图形可以密铺?给可以密铺的图形打“√”。
( ) ( ) ( )
( ) ( ) ( )
√
√
√
√
课堂练习
下面三幅图哪幅是密铺 给是密铺的图形打“√”。
( ) ( ) ( )
√
√
课堂练习
仔细观察下面的图,它们是由哪些基本图形密铺形成的?在下面画出这个基本图形。
课堂练习
拓展应用:(1)算一算,并说说为什么正五边形不能密铺?
正五边形内角和:3×180°=540°
每个角的度数:540°÷5=108°
108°×3=324° 324°<360°
所以正五边形不能密铺。
课堂练习
拓展应用:(2)算一算,并说说为什么正六边形能密铺?
正六边形内角和:4×180°=720°
每个角的度数:720°÷6=120°
120°×3=360°
所以正六边形能密铺。
课堂总结
通过今天的学习,你有哪些收获?
我知道图形之间没有空隙,也不重叠,是密铺。
我还会判断哪些图形可以密铺。
板书设计
密 铺
无空隙 不重叠
三角形、四边形、正六边形可以密铺
圆、正五边形不能密铺
作业布置
利用一种图形或几种图形设计一幅密铺图案。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
