人教版数学八年级上册15.1.1 从分数到分式 课件(21张ppt)
文档属性
| 名称 | 人教版数学八年级上册15.1.1 从分数到分式 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 454.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 21:04:03 | ||
图片预览







文档简介
(共21张PPT)
15.1.1从分数到分式
学习目标
1.理解并掌握分式的概念,会判断一个代数式是否为分式.
2.理解分式有意义的条件及分式值为零的条件.
3.能熟练地求出分式有意义的条件及分式的值为零 的条件.
(1)如果乐乐的速度是13米/秒,那么她所用的时间是( )秒;
(2)如果乐乐的速度是a米/秒,那么她所用的时间是( )秒;
(3)如果乐乐原来的速度是a米/秒,经过训练她的速度每秒增加
了1米,那么她现在所用的时间是( )秒.
填空:乐乐同学参加百米赛跑,
情境导入
(4)若把体积为200 cm3的水倒入底面积为33 cm2的圆柱形保温桶中,水面高度为( )cm;若把体积为V 的水倒入底面积为S 的圆柱形容器中,水面高度为( ).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,
合计为 元.
(8a+b)
情境导入
问题1:请将上面问题中得到的式子分分类:
单项式:
多项式:
8a+b
整
式
探索新知
问题2 请大家观察式子
它们与分数( )有什么相同点和不同点?
都具有 的形式
相同点
(从形式看)
不同点
(观察分母分子)
分数的分子A与分母B都是整数;
而这些式子分子A与分母B都是整式,并且分母B中都含有字母
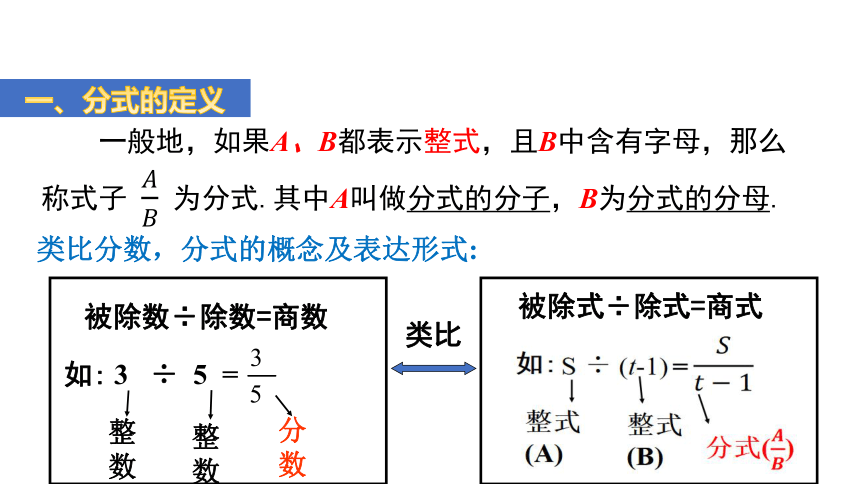
类比分数,分式的概念及表达形式:
整数
整数
分数
类比
3 ÷ 5 =
被除数÷除数=商数
如:
一般地,如果A、B都表示整式,且B中含有字母,那么称式子 为分式.其中A叫做分式的分子,B为分式的分母.
一、分式的定义
被除式÷除式=商式
认识分式
分式比分数更具有一般性,
也是不同于整式的另一类式子。
观察下列一组数的规律,表示出第n个数是多少?
, , , ,……,
(n为正整数)
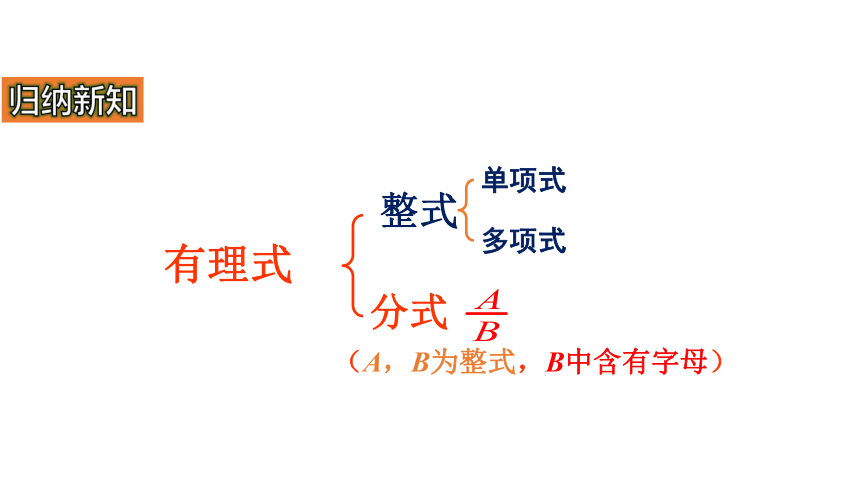
单项式
多项式
有理式
(A,B为整式,B中含有字母)
分式
整式
归纳新知
1.下列各式哪些是分式?
分式
分式
分式
分式
针对练习
分式
在分式 中,
知识精讲
二、分式有(无)意义的条件:
对于分式 ,
当_______时分式有意义;
当_______时分式无意义.
B≠0
B=0
分母B的值不能是0,
如果分母的值是0,分式没有意义。
例1 下列分式中x取什么值,分式有意义?
解:(1)分母 ,即 ;
典例解析
(2)分母 ,即 ;
(3)分母 ,即 .
例2 已知分式 有意义,则x应满足的条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠-2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
典例解析
(1)
(2)
(3)
(5)
(4)
针对练习
2.下列各式中,x为何值时,该分式有意义
想一想:分式 的值为零应满足什么条件?
当A=0而 B≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
三、分式值为零的条件
分析:当分子等于零而分母不等于零时,分式的值为零.
例3 当x为何值时,分式 的值为零
典例解析
3.当分式 的值为零时,求x的值。
针对练习
小结梳理
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
巩固提高
2.当x为任意实数时,下列分式一定有意义的是( )
A
4.已知,当x=5时,分式 的值等于零,则k .
=-10
5.若分式 的值为零,则x的值为多少?
6.当x 时,分式
巩固提高
3.当x=-3时分式中没有意义的是( )
C
15.1.1从分数到分式
学习目标
1.理解并掌握分式的概念,会判断一个代数式是否为分式.
2.理解分式有意义的条件及分式值为零的条件.
3.能熟练地求出分式有意义的条件及分式的值为零 的条件.
(1)如果乐乐的速度是13米/秒,那么她所用的时间是( )秒;
(2)如果乐乐的速度是a米/秒,那么她所用的时间是( )秒;
(3)如果乐乐原来的速度是a米/秒,经过训练她的速度每秒增加
了1米,那么她现在所用的时间是( )秒.
填空:乐乐同学参加百米赛跑,
情境导入
(4)若把体积为200 cm3的水倒入底面积为33 cm2的圆柱形保温桶中,水面高度为( )cm;若把体积为V 的水倒入底面积为S 的圆柱形容器中,水面高度为( ).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,
合计为 元.
(8a+b)
情境导入
问题1:请将上面问题中得到的式子分分类:
单项式:
多项式:
8a+b
整
式
探索新知
问题2 请大家观察式子
它们与分数( )有什么相同点和不同点?
都具有 的形式
相同点
(从形式看)
不同点
(观察分母分子)
分数的分子A与分母B都是整数;
而这些式子分子A与分母B都是整式,并且分母B中都含有字母
类比分数,分式的概念及表达形式:
整数
整数
分数
类比
3 ÷ 5 =
被除数÷除数=商数
如:
一般地,如果A、B都表示整式,且B中含有字母,那么称式子 为分式.其中A叫做分式的分子,B为分式的分母.
一、分式的定义
被除式÷除式=商式
认识分式
分式比分数更具有一般性,
也是不同于整式的另一类式子。
观察下列一组数的规律,表示出第n个数是多少?
, , , ,……,
(n为正整数)
单项式
多项式
有理式
(A,B为整式,B中含有字母)
分式
整式
归纳新知
1.下列各式哪些是分式?
分式
分式
分式
分式
针对练习
分式
在分式 中,
知识精讲
二、分式有(无)意义的条件:
对于分式 ,
当_______时分式有意义;
当_______时分式无意义.
B≠0
B=0
分母B的值不能是0,
如果分母的值是0,分式没有意义。
例1 下列分式中x取什么值,分式有意义?
解:(1)分母 ,即 ;
典例解析
(2)分母 ,即 ;
(3)分母 ,即 .
例2 已知分式 有意义,则x应满足的条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠-2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
典例解析
(1)
(2)
(3)
(5)
(4)
针对练习
2.下列各式中,x为何值时,该分式有意义
想一想:分式 的值为零应满足什么条件?
当A=0而 B≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
三、分式值为零的条件
分析:当分子等于零而分母不等于零时,分式的值为零.
例3 当x为何值时,分式 的值为零
典例解析
3.当分式 的值为零时,求x的值。
针对练习
小结梳理
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
巩固提高
2.当x为任意实数时,下列分式一定有意义的是( )
A
4.已知,当x=5时,分式 的值等于零,则k .
=-10
5.若分式 的值为零,则x的值为多少?
6.当x 时,分式
巩固提高
3.当x=-3时分式中没有意义的是( )
C
