人教版数学八年级下册18.1.1 平行四边形的性质 同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的性质 同步练习(含解析) | 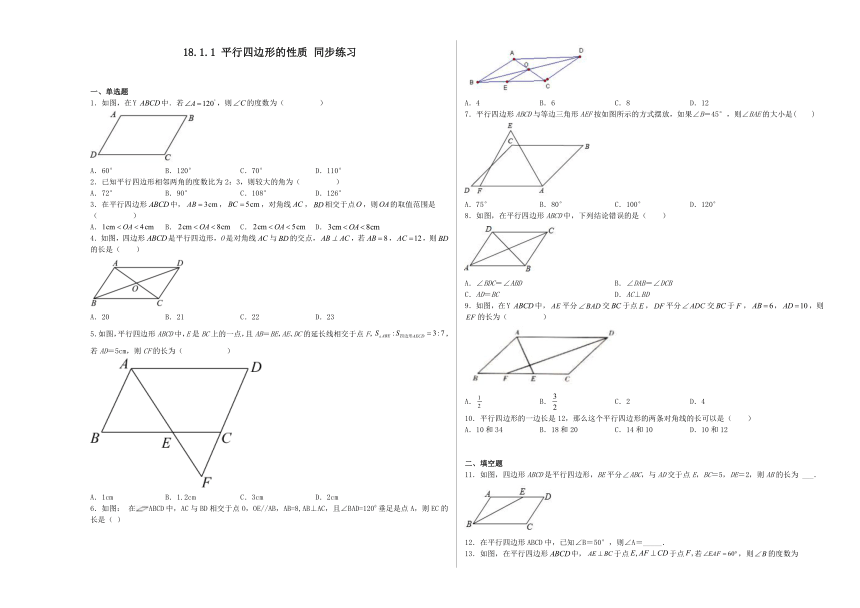 | |
| 格式 | zip | ||
| 文件大小 | 361.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 21:11:01 | ||
图片预览




文档简介
18.1.1 平行四边形的性质 同步练习
一、单选题
1.如图,在中.若,则的度数为( )
A.60° B.120° C.70° D.110°
2.已知平行四边形相邻两角的度数比为2:3,则较大的角为( )
A.72° B.90° C.108° D.126°
3.在平行四边形中,,,对角线,相交于点,则的取值范围是( )
A. B. C. D.
4.如图,四边形是平行四边形,O是对角线与的交点,,若,,则的长是( )
A.20 B.21 C.22 D.23
5.如图,平行四边形ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,,若AD=5cm,则CF的长为( )
A.1cm B.1.2cm C.3cm D.2cm
6.如图: 在ABCD中,AC与BD相交于点O,OE//AB,AB=8,AB⊥AC,且∠BAD=1200 垂足是点A,则EC的长是( )
A.4 B.6 C.8 D.12
7.平行四边形ABCD与等边三角形AEF按如图所示的方式摆放,如果∠B=45°,则∠BAE的大小是( )
A.75° B.80° C.100° D.120°
8.如图,在平行四边形ABCD中,下列结论错误的是( )
A.∠BDC=∠ABD B.∠DAB=∠DCB
C.AD=BC D.AC⊥BD
9.如图,在中,平分交于点,平分交于,,,则的长为( )
A. B. C.2 D.4
10.平行四边形的一边长是12,那么这个平行四边形的两条对角线的长可以是( )
A.10和34 B.18和20 C.14和10 D.10和12
二、填空题
11.如图,四边形ABCD是平行四边形,BE平分∠ABC,与AD交于点E,BC=5,DE=2,则AB的长为 ___.
12.在平行四边形ABCD中,已知∠B=50°,则∠A=_____.
13.如图,在平行四边形中,于点于点若,则的度数为_____________________.
14.如图,点E为平行四边形ABCD内一点,连接EA,EB,EC,AC,已知△BCE的面积为2,△ABE的面积为3,△CED的面积为10,则△ADE的面积为 ___,阴影部分的面积为 ___.
15.如图,在中,为边的中点,联结,与对角线相交于点,则与四边形的面积比为_______.
三、解答题
16.已知:中,,AE平分交BC于E点.
(1)求的度数;
(2)求的度数.
17.如图,AC是平行四边形ABCD的对角线.
(1)尺规作图:作线段AC的垂直平分线EG,分别交AB,AC,CD于点E,F,G.(不写作法,保留作图痕迹);
(2)在(1)的条件下,猜想DG与BE存在的数量关系,并证明你猜想的结论.
18.如图,已知平行四边形ABCD.
(1)用直尺和圆规作出∠ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
参考答案
1.B
【详解】解:∵四边形 是平行四边形,
∴ ,
∵,
∴ .
故选:B.
2.C
【详解】解:四边形是平行四边形,
,
,
,
,
故选:C.
3.A
【详解】解:∵AB=3cm,BC=5cm,
∴2cm<AC<8cm,
∵四边形ABCD是平行四边形,
∴AO=AC,
∴1cm<OA<4cm,
故选:A.
4.A
【详解】解:∵四边形是平行四边形,,
∴,
∵,,
∴,
∴.
故选:A.
5.D
【详解】解:连接AC,
在平行四边形ABCD中,
∴S△ABC=S△ADC,AD=BC,AB=CD,AB∥CD,
∵S△ABE:S四边形AECD=3:7,即S△ABE:S四边形ABCD=3:10,
∴S△ABE:S△ABC=3:5,
∴BE:BC=3:5,
∵AD=5cm,
∴AD=BC=5cm,
∴BE=3cm,EC=BC-BE=2(cm),
∵AB=BE,AB∥CD,
∴∠BAE=∠BEA,∠BAE=∠F,
又∠CEF=∠BEA,
∴∠CEF=∠F,
∴CE=CF=2(cm),
故选:D.
6.C
【详解】试题分析:因为OE//AB,AB=8,O为AC的中点,所以OE为△ABC的中位线,故OE=4,AB⊥AC,所以∠EOC=∠BAC=90°,又因为∠BAD=120°,所以∠DAC=30°,AD∥BC,所以
∠BCA=∠DAC=30°,所以CE=2OE=8.故选C.
7.A
【详解】解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠BAD=180°-∠B=180°-45°=135°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠BAE=∠BAD-∠EAF=75°.
故选:A.
8.D
【详解】∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BDC=∠ABD,故选项A正确;
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,故选项B正确;
∵四边形ABCD是平行四边形,
∴AD=BC,故选项C正确;
由四边形ABCD是平行四边形,不一定得出AC⊥BD,
故选D.
9.C
【详解】∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=6,BC=AD=10,
∴∠DAE=∠AEB,∠ADF=∠CFD,
∵AE、DF分别平分∠BAD、∠ADC,
∴∠DAE=∠BAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CDF=∠CFD,
∴AB=BE,CD=CF,
∴BE=CF=6;
∴EF=BE+CF-BC=6+6-10=2.
故选:C
10.B
【详解】解:如图,作CE∥BD,交AB的延长线于点E,
∵AB=CD,DC∥AB
∴四边形BECD是平行四边形,
∴CE=BD,BE=CD=AB,
∴在△ACE中,AE=2AB=24<AC+CE,
∴四个选项中只有A,B符合条件,但是10,34,24不符合三边关系,
故选:B.
11.
【详解】解:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
∵,BE平分,
∴,,
∴,
∴,
故答案为:3.
12.
【详解】解:∵在 ABCD中∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故答案为:130°.
13.
【详解】解:∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
在四边形AECF中,∠C=360°﹣∠EAF﹣∠AEC﹣∠AFC=360°﹣60°﹣90°﹣90°=120°,
在 ABCD中,∠B=180°﹣∠C=180°﹣120°=60°.
故答案为:60°.
14.
【详解】解:∵四边形ABCD是平行四边形,
∴,
∴△ADE的面积为=3+10-2=11;
∴=2+3+10+11=26,
∴阴影部分的面积为,
故答案为:11,8.
15.
【详解】解:设的面积为S,
在中,AD=BC,AD//BC,
为边的中点,
故答案为:.
16.
(1)
解:∵ABCD是平行四边形,
∴AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=52°,
∴∠BAD=180°-52°=128°,
(2)
解:∵AE平分∠BAD,
∴∠BAE=∠DAE=∠BAD=64°;
∵AD∥BC,
∴∠DAE+∠AEC=180°,
∴∠AEC=180°-64°=116°;
17.
(1)
解:如图,直线l为所作;
(2)
DG=BE,理由如下:
∵EG垂直平分AC,
∴FA=FC,
∵四边形ABCD为平行四边形,
∴CD∥AB,CD=AB,
∴∠DCA=∠BAC,
在△CFG和△AFE中,
,
∴△CFG≌△AFE(ASA),
∴CG=AE,
∴CD-CG=AB-AE,
即DG=BE.
18.
【详解】(1)解:如图所示,即为所求;
(2)解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠CBF=∠E,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠E,
∴AE=AB,
∴△ABE是等腰三角形;
(3)解:由(2)得∠ABF=∠CFB=∠CBF,∠E=∠ABF,
∴CF=CB,
∴△CBF是等腰三角形;
∵∠EFD=∠CFB,
∴∠E=∠EFD,
∴DE=DF,
∴△DEF是等腰三角形
一、单选题
1.如图,在中.若,则的度数为( )
A.60° B.120° C.70° D.110°
2.已知平行四边形相邻两角的度数比为2:3,则较大的角为( )
A.72° B.90° C.108° D.126°
3.在平行四边形中,,,对角线,相交于点,则的取值范围是( )
A. B. C. D.
4.如图,四边形是平行四边形,O是对角线与的交点,,若,,则的长是( )
A.20 B.21 C.22 D.23
5.如图,平行四边形ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,,若AD=5cm,则CF的长为( )
A.1cm B.1.2cm C.3cm D.2cm
6.如图: 在ABCD中,AC与BD相交于点O,OE//AB,AB=8,AB⊥AC,且∠BAD=1200 垂足是点A,则EC的长是( )
A.4 B.6 C.8 D.12
7.平行四边形ABCD与等边三角形AEF按如图所示的方式摆放,如果∠B=45°,则∠BAE的大小是( )
A.75° B.80° C.100° D.120°
8.如图,在平行四边形ABCD中,下列结论错误的是( )
A.∠BDC=∠ABD B.∠DAB=∠DCB
C.AD=BC D.AC⊥BD
9.如图,在中,平分交于点,平分交于,,,则的长为( )
A. B. C.2 D.4
10.平行四边形的一边长是12,那么这个平行四边形的两条对角线的长可以是( )
A.10和34 B.18和20 C.14和10 D.10和12
二、填空题
11.如图,四边形ABCD是平行四边形,BE平分∠ABC,与AD交于点E,BC=5,DE=2,则AB的长为 ___.
12.在平行四边形ABCD中,已知∠B=50°,则∠A=_____.
13.如图,在平行四边形中,于点于点若,则的度数为_____________________.
14.如图,点E为平行四边形ABCD内一点,连接EA,EB,EC,AC,已知△BCE的面积为2,△ABE的面积为3,△CED的面积为10,则△ADE的面积为 ___,阴影部分的面积为 ___.
15.如图,在中,为边的中点,联结,与对角线相交于点,则与四边形的面积比为_______.
三、解答题
16.已知:中,,AE平分交BC于E点.
(1)求的度数;
(2)求的度数.
17.如图,AC是平行四边形ABCD的对角线.
(1)尺规作图:作线段AC的垂直平分线EG,分别交AB,AC,CD于点E,F,G.(不写作法,保留作图痕迹);
(2)在(1)的条件下,猜想DG与BE存在的数量关系,并证明你猜想的结论.
18.如图,已知平行四边形ABCD.
(1)用直尺和圆规作出∠ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
参考答案
1.B
【详解】解:∵四边形 是平行四边形,
∴ ,
∵,
∴ .
故选:B.
2.C
【详解】解:四边形是平行四边形,
,
,
,
,
故选:C.
3.A
【详解】解:∵AB=3cm,BC=5cm,
∴2cm<AC<8cm,
∵四边形ABCD是平行四边形,
∴AO=AC,
∴1cm<OA<4cm,
故选:A.
4.A
【详解】解:∵四边形是平行四边形,,
∴,
∵,,
∴,
∴.
故选:A.
5.D
【详解】解:连接AC,
在平行四边形ABCD中,
∴S△ABC=S△ADC,AD=BC,AB=CD,AB∥CD,
∵S△ABE:S四边形AECD=3:7,即S△ABE:S四边形ABCD=3:10,
∴S△ABE:S△ABC=3:5,
∴BE:BC=3:5,
∵AD=5cm,
∴AD=BC=5cm,
∴BE=3cm,EC=BC-BE=2(cm),
∵AB=BE,AB∥CD,
∴∠BAE=∠BEA,∠BAE=∠F,
又∠CEF=∠BEA,
∴∠CEF=∠F,
∴CE=CF=2(cm),
故选:D.
6.C
【详解】试题分析:因为OE//AB,AB=8,O为AC的中点,所以OE为△ABC的中位线,故OE=4,AB⊥AC,所以∠EOC=∠BAC=90°,又因为∠BAD=120°,所以∠DAC=30°,AD∥BC,所以
∠BCA=∠DAC=30°,所以CE=2OE=8.故选C.
7.A
【详解】解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠BAD=180°-∠B=180°-45°=135°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠BAE=∠BAD-∠EAF=75°.
故选:A.
8.D
【详解】∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BDC=∠ABD,故选项A正确;
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,故选项B正确;
∵四边形ABCD是平行四边形,
∴AD=BC,故选项C正确;
由四边形ABCD是平行四边形,不一定得出AC⊥BD,
故选D.
9.C
【详解】∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=6,BC=AD=10,
∴∠DAE=∠AEB,∠ADF=∠CFD,
∵AE、DF分别平分∠BAD、∠ADC,
∴∠DAE=∠BAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CDF=∠CFD,
∴AB=BE,CD=CF,
∴BE=CF=6;
∴EF=BE+CF-BC=6+6-10=2.
故选:C
10.B
【详解】解:如图,作CE∥BD,交AB的延长线于点E,
∵AB=CD,DC∥AB
∴四边形BECD是平行四边形,
∴CE=BD,BE=CD=AB,
∴在△ACE中,AE=2AB=24<AC+CE,
∴四个选项中只有A,B符合条件,但是10,34,24不符合三边关系,
故选:B.
11.
【详解】解:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
∵,BE平分,
∴,,
∴,
∴,
故答案为:3.
12.
【详解】解:∵在 ABCD中∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故答案为:130°.
13.
【详解】解:∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
在四边形AECF中,∠C=360°﹣∠EAF﹣∠AEC﹣∠AFC=360°﹣60°﹣90°﹣90°=120°,
在 ABCD中,∠B=180°﹣∠C=180°﹣120°=60°.
故答案为:60°.
14.
【详解】解:∵四边形ABCD是平行四边形,
∴,
∴△ADE的面积为=3+10-2=11;
∴=2+3+10+11=26,
∴阴影部分的面积为,
故答案为:11,8.
15.
【详解】解:设的面积为S,
在中,AD=BC,AD//BC,
为边的中点,
故答案为:.
16.
(1)
解:∵ABCD是平行四边形,
∴AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=52°,
∴∠BAD=180°-52°=128°,
(2)
解:∵AE平分∠BAD,
∴∠BAE=∠DAE=∠BAD=64°;
∵AD∥BC,
∴∠DAE+∠AEC=180°,
∴∠AEC=180°-64°=116°;
17.
(1)
解:如图,直线l为所作;
(2)
DG=BE,理由如下:
∵EG垂直平分AC,
∴FA=FC,
∵四边形ABCD为平行四边形,
∴CD∥AB,CD=AB,
∴∠DCA=∠BAC,
在△CFG和△AFE中,
,
∴△CFG≌△AFE(ASA),
∴CG=AE,
∴CD-CG=AB-AE,
即DG=BE.
18.
【详解】(1)解:如图所示,即为所求;
(2)解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠CBF=∠E,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠E,
∴AE=AB,
∴△ABE是等腰三角形;
(3)解:由(2)得∠ABF=∠CFB=∠CBF,∠E=∠ABF,
∴CF=CB,
∴△CBF是等腰三角形;
∵∠EFD=∠CFB,
∴∠E=∠EFD,
∴DE=DF,
∴△DEF是等腰三角形
