第七章 平面直角坐标系单元质量检测试卷A(含答案)
文档属性
| 名称 | 第七章 平面直角坐标系单元质量检测试卷A(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:27:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2022-20203年七年级(下)第七章平面直角坐标系检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如果把电影票上 排 座记作 ,那么 表示
A. 排 座 B. 排 座 C. 排 座 D. 排 座
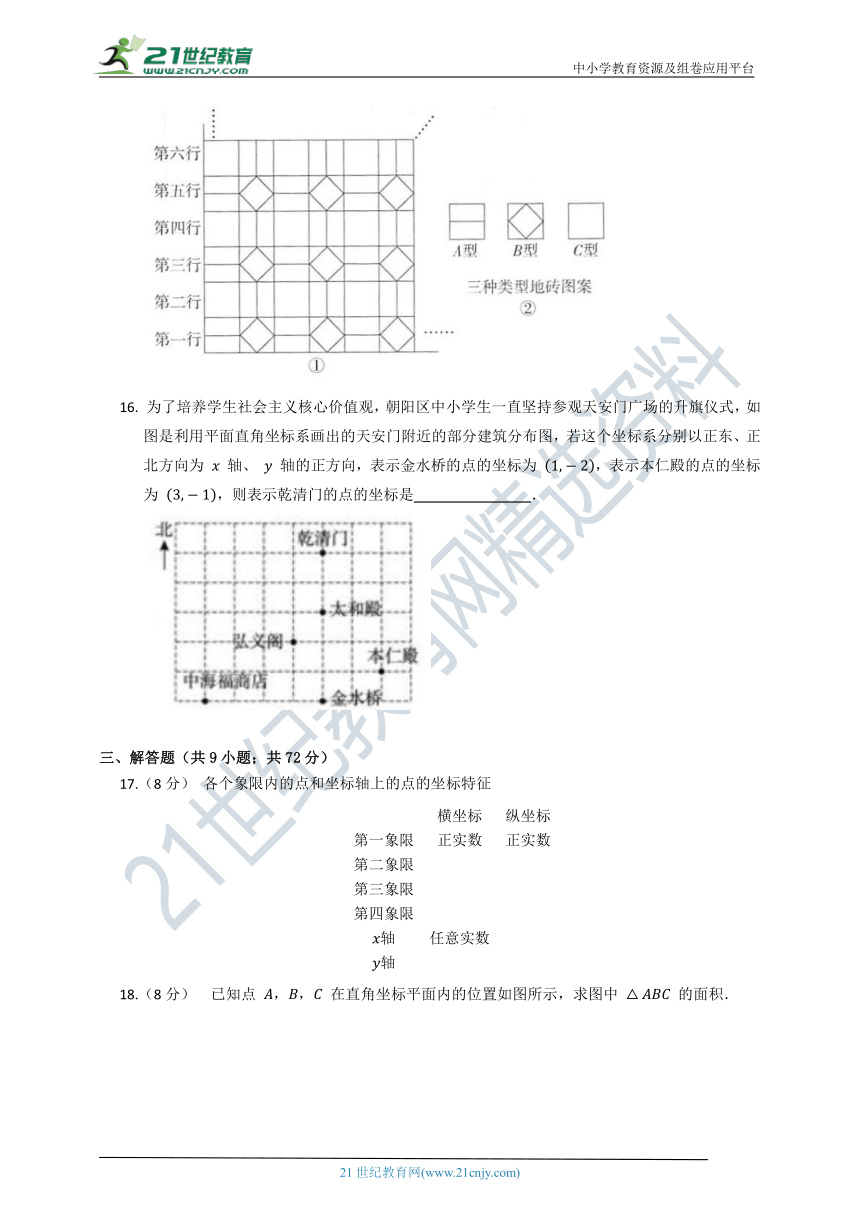
2. 如图,,,,,, 按此规律,点 的坐标为
A. B.
C. D.
3. 如图,在平面直角坐标系中,线段 的两个端点是 ,.将线段 沿某一方向平移后,若点 的对应点 的坐标为 ,则点 的对应点 的坐标为
A. B. C. D.
4. 在平面直角坐标系中,点 满足 ,则 的位置是
A. 轴 B. 原点 C. 轴 D. 坐标轴
5. 过点 且垂直于 轴的直线交 轴于点 ,则点 的坐标为
A. B. C. D.
6. 将点 沿 轴向左平移 个单位长度得到点 ,点 的坐标为
A. B. C. D.
7. 已知:点 ,, 为坐标原点,则 的面积为
A. B. C. D.
8. 经过点 垂直于 轴的直线可以表示为
A. 直线 B. 直线 C. 直线 D. 直线
9. 点 向下平移 个单位到点 ,若 在 轴上,则点 的坐标是
A. B. C. D.
10. 如图所示,雷达探测器测得六个目标 ,,,,, 出现,按照规定的目标表示法,目标 , 的位置分别表 ,.按照此方法表示目标 ,,, 的位置,不正确的是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 将点 向左平移 个单位,再向下平移 个单位后得到对应点的坐标是 .
12. 一个点从 沿 轴正方向平移 个单位,然后沿着 轴平行的方向向下平移 个单位到达点 ,那么点 的坐标是 .
13. 某学校的教学大楼的教室是按一定规律编号的,如果教室 是指该教学楼中第 层第 个教室,那么第 层第 个教室的编号是 .
14. 描述一个平移的要素是 和 .
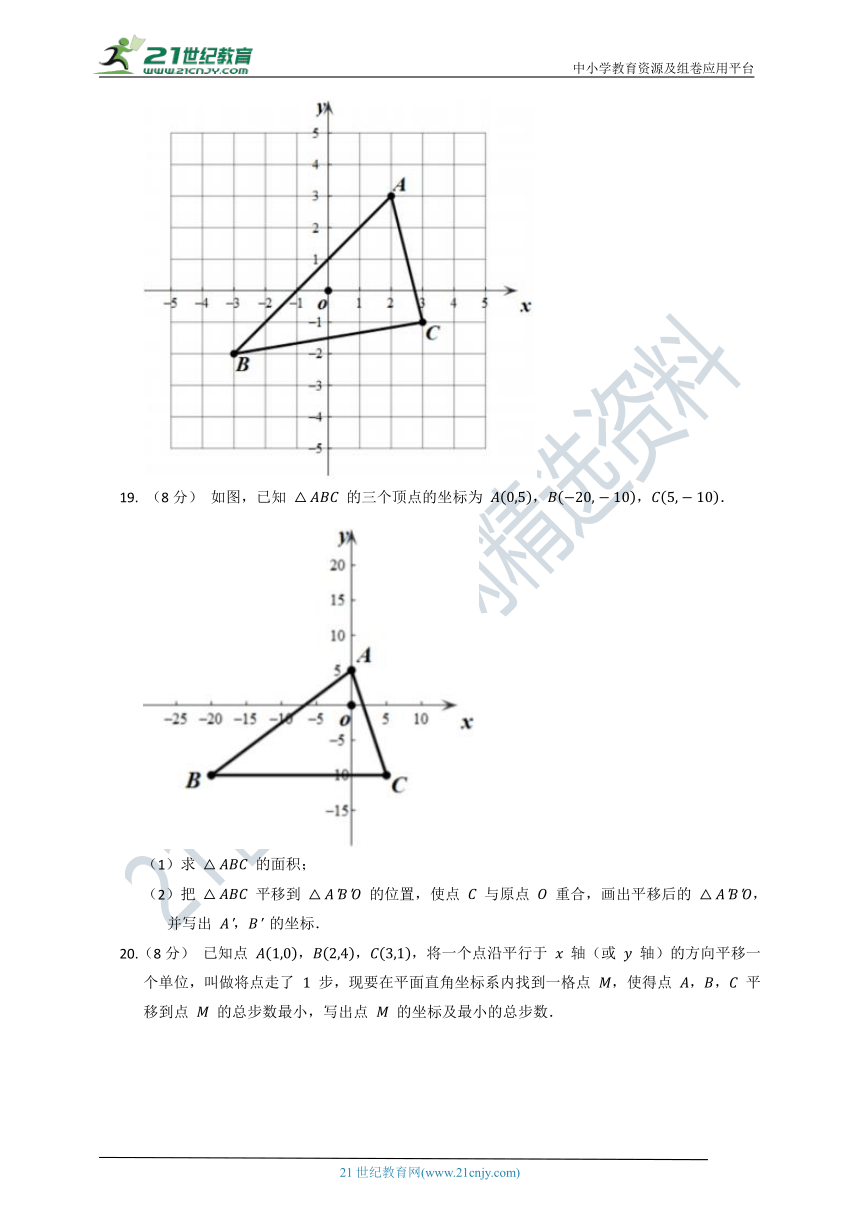
15. 如图①,某广场地面是用 ,, 三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块( 型)地砖的位置记作 ,第二块( 型)地砖的位置记作 ,,若 位置恰好为 型地砖,则正整数 , 须满足的条件是 .
16. 为了培养学生社会主义核心价值观,朝阳区中小学生一直坚持参观天安门广场的升旗仪式,如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示金水桥的点的坐标为 ,表示本仁殿的点的坐标为 ,则表示乾清门的点的坐标是 .
三、解答题(共9小题;共72分)
17.(8分) 各个象限内的点和坐标轴上的点的坐标特征
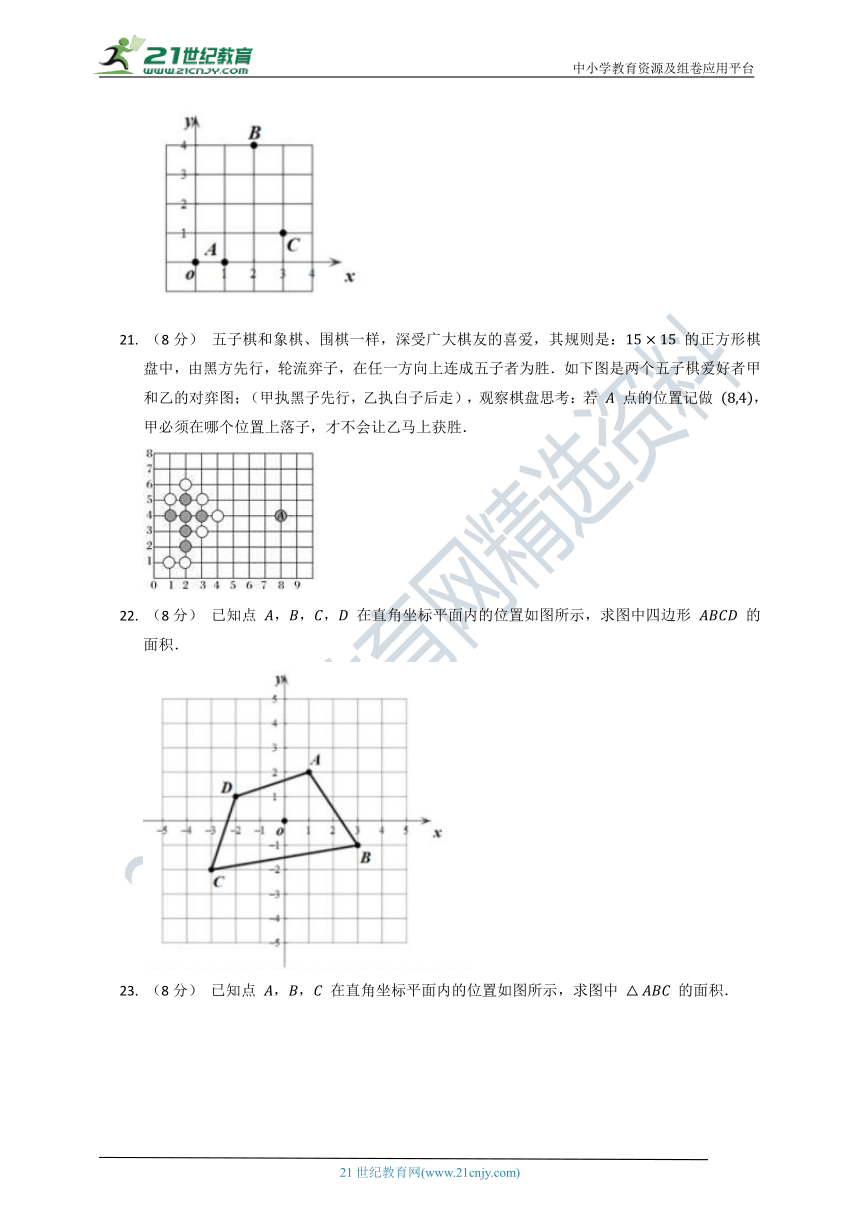
18.(8分) 已知点 ,, 在直角坐标平面内的位置如图所示,求图中 的面积.
19. (8分) 如图,已知 的三个顶点的坐标为 ,,.
(1)求 的面积;
(2)把 平移到 的位置,使点 与原点 重合,画出平移后的 ,并写出 , 的坐标.
20.(8分) 已知点 ,,,将一个点沿平行于 轴(或 轴)的方向平移一个单位,叫做将点走了 步,现要在平面直角坐标系内找到一格点 ,使得点 ,, 平移到点 的总步数最小,写出点 的坐标及最小的总步数.
21. (8分) 五子棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是: 的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如下图是两个五子棋爱好者甲和乙的对弈图;(甲执黑子先行,乙执白子后走),观察棋盘思考:若 点的位置记做 ,甲必须在哪个位置上落子,才不会让乙马上获胜.
22. (8分) 已知点 ,,, 在直角坐标平面内的位置如图所示,求图中四边形 的面积.
23. (8分) 已知点 ,, 在直角坐标平面内的位置如图所示,求图中 的面积.
24. (8分) 直线 轴,直线 轴,已知点 ,,,且点 的横坐标比纵坐标小 ,求 ,, 各点坐标.
25. (8分) 如图是某市区的平面图, 地的坐标是 .
(1)在平面图上画出直角坐标系;
(2)写出 地、 地、 地、 地的坐标;
(3)标出坐标为 的地点 .
答案
一
1. C
【解析】在电影票上,“ 排 座”记作 ,则那么 表示“ 排 座”.
故选:C.
2. B
【解析】由题可知:
第一象限的点:,, 角标除以 余数为 ;
第二象限的点:,, 角标除以 余数为 ;
第三象限的点:,, 角标除以 余数为 ;
第四象限的点:,, 角标除以 余数为 ;
由上规律可知:,
所以点 在第四象限,纵坐标为 ,横坐标为 ,
所以 的坐标是 .
3. C
4. D
【解析】 点 且 ,
或 ,
如果 ,点 在 轴上;
如果 ,点 在 轴上;
如果 ,,则点在坐标原点.
所以点 在坐标轴上.
故选:D.
5. C
【解析】如图所示:
过点 且垂直于 轴的直线交 轴于点 ,故点 的坐标为:.
故选:C.
6. D
7. C
8. C
【解析】经过点 且垂直于 轴的直线可以表示为直线 .
故选:C.
9. C
10. D
二
11.
12.
13.
14. 距离大小,方向
15. , 同为奇数或 , 同为偶数
【解析】观察题图, 型地砖在列数为奇数,行数也为奇数的位置上或列数为偶数,行数也为偶数的位置上,若 位置恰好为 型地砖,则正整数 , 须满足的条件为 , 同为奇数或 , 同为偶数.
16.
三
17.
18. 画出梯形 ,点 ,,,, 的坐标分别为 ,,,,,
因此 ,,,,,所以 的面积 .
19. (1) .
(2) ,.
20. ; 步
21. 白棋已经有三个在一条直线上,
甲必须在 或 位置上落子,才不会让乙马上获胜.
22.
23. 过 作 ,点 ,,, 的坐标分别为 ,,,,因此 ,,所以 的面积 .
24. ,,.
25. (1) 坐标系如图所示.
(2) ,,,.
(3) 地点 如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2022-20203年七年级(下)第七章平面直角坐标系检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如果把电影票上 排 座记作 ,那么 表示
A. 排 座 B. 排 座 C. 排 座 D. 排 座
2. 如图,,,,,, 按此规律,点 的坐标为
A. B.
C. D.
3. 如图,在平面直角坐标系中,线段 的两个端点是 ,.将线段 沿某一方向平移后,若点 的对应点 的坐标为 ,则点 的对应点 的坐标为
A. B. C. D.
4. 在平面直角坐标系中,点 满足 ,则 的位置是
A. 轴 B. 原点 C. 轴 D. 坐标轴
5. 过点 且垂直于 轴的直线交 轴于点 ,则点 的坐标为
A. B. C. D.
6. 将点 沿 轴向左平移 个单位长度得到点 ,点 的坐标为
A. B. C. D.
7. 已知:点 ,, 为坐标原点,则 的面积为
A. B. C. D.
8. 经过点 垂直于 轴的直线可以表示为
A. 直线 B. 直线 C. 直线 D. 直线
9. 点 向下平移 个单位到点 ,若 在 轴上,则点 的坐标是
A. B. C. D.
10. 如图所示,雷达探测器测得六个目标 ,,,,, 出现,按照规定的目标表示法,目标 , 的位置分别表 ,.按照此方法表示目标 ,,, 的位置,不正确的是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 将点 向左平移 个单位,再向下平移 个单位后得到对应点的坐标是 .
12. 一个点从 沿 轴正方向平移 个单位,然后沿着 轴平行的方向向下平移 个单位到达点 ,那么点 的坐标是 .
13. 某学校的教学大楼的教室是按一定规律编号的,如果教室 是指该教学楼中第 层第 个教室,那么第 层第 个教室的编号是 .
14. 描述一个平移的要素是 和 .
15. 如图①,某广场地面是用 ,, 三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块( 型)地砖的位置记作 ,第二块( 型)地砖的位置记作 ,,若 位置恰好为 型地砖,则正整数 , 须满足的条件是 .
16. 为了培养学生社会主义核心价值观,朝阳区中小学生一直坚持参观天安门广场的升旗仪式,如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示金水桥的点的坐标为 ,表示本仁殿的点的坐标为 ,则表示乾清门的点的坐标是 .
三、解答题(共9小题;共72分)
17.(8分) 各个象限内的点和坐标轴上的点的坐标特征
18.(8分) 已知点 ,, 在直角坐标平面内的位置如图所示,求图中 的面积.
19. (8分) 如图,已知 的三个顶点的坐标为 ,,.
(1)求 的面积;
(2)把 平移到 的位置,使点 与原点 重合,画出平移后的 ,并写出 , 的坐标.
20.(8分) 已知点 ,,,将一个点沿平行于 轴(或 轴)的方向平移一个单位,叫做将点走了 步,现要在平面直角坐标系内找到一格点 ,使得点 ,, 平移到点 的总步数最小,写出点 的坐标及最小的总步数.
21. (8分) 五子棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是: 的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如下图是两个五子棋爱好者甲和乙的对弈图;(甲执黑子先行,乙执白子后走),观察棋盘思考:若 点的位置记做 ,甲必须在哪个位置上落子,才不会让乙马上获胜.
22. (8分) 已知点 ,,, 在直角坐标平面内的位置如图所示,求图中四边形 的面积.
23. (8分) 已知点 ,, 在直角坐标平面内的位置如图所示,求图中 的面积.
24. (8分) 直线 轴,直线 轴,已知点 ,,,且点 的横坐标比纵坐标小 ,求 ,, 各点坐标.
25. (8分) 如图是某市区的平面图, 地的坐标是 .
(1)在平面图上画出直角坐标系;
(2)写出 地、 地、 地、 地的坐标;
(3)标出坐标为 的地点 .
答案
一
1. C
【解析】在电影票上,“ 排 座”记作 ,则那么 表示“ 排 座”.
故选:C.
2. B
【解析】由题可知:
第一象限的点:,, 角标除以 余数为 ;
第二象限的点:,, 角标除以 余数为 ;
第三象限的点:,, 角标除以 余数为 ;
第四象限的点:,, 角标除以 余数为 ;
由上规律可知:,
所以点 在第四象限,纵坐标为 ,横坐标为 ,
所以 的坐标是 .
3. C
4. D
【解析】 点 且 ,
或 ,
如果 ,点 在 轴上;
如果 ,点 在 轴上;
如果 ,,则点在坐标原点.
所以点 在坐标轴上.
故选:D.
5. C
【解析】如图所示:
过点 且垂直于 轴的直线交 轴于点 ,故点 的坐标为:.
故选:C.
6. D
7. C
8. C
【解析】经过点 且垂直于 轴的直线可以表示为直线 .
故选:C.
9. C
10. D
二
11.
12.
13.
14. 距离大小,方向
15. , 同为奇数或 , 同为偶数
【解析】观察题图, 型地砖在列数为奇数,行数也为奇数的位置上或列数为偶数,行数也为偶数的位置上,若 位置恰好为 型地砖,则正整数 , 须满足的条件为 , 同为奇数或 , 同为偶数.
16.
三
17.
18. 画出梯形 ,点 ,,,, 的坐标分别为 ,,,,,
因此 ,,,,,所以 的面积 .
19. (1) .
(2) ,.
20. ; 步
21. 白棋已经有三个在一条直线上,
甲必须在 或 位置上落子,才不会让乙马上获胜.
22.
23. 过 作 ,点 ,,, 的坐标分别为 ,,,,因此 ,,所以 的面积 .
24. ,,.
25. (1) 坐标系如图所示.
(2) ,,,.
(3) 地点 如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
