第七章 平面直角坐标系单元质量检测试卷C(含答案)
文档属性
| 名称 | 第七章 平面直角坐标系单元质量检测试卷C(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 19:28:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2022-2023学年七年级(下)第七章平面直角坐标系检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 直角坐标平面上的点 通过上下平移不能与之重合的是
A. B. C. D.
2. 对于任何实数 ,点 一定不在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、 正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是
A. 滑雪大跳台 B. 五一剧场
C. 冬奥组委会 D. 全民畅读艺术书店
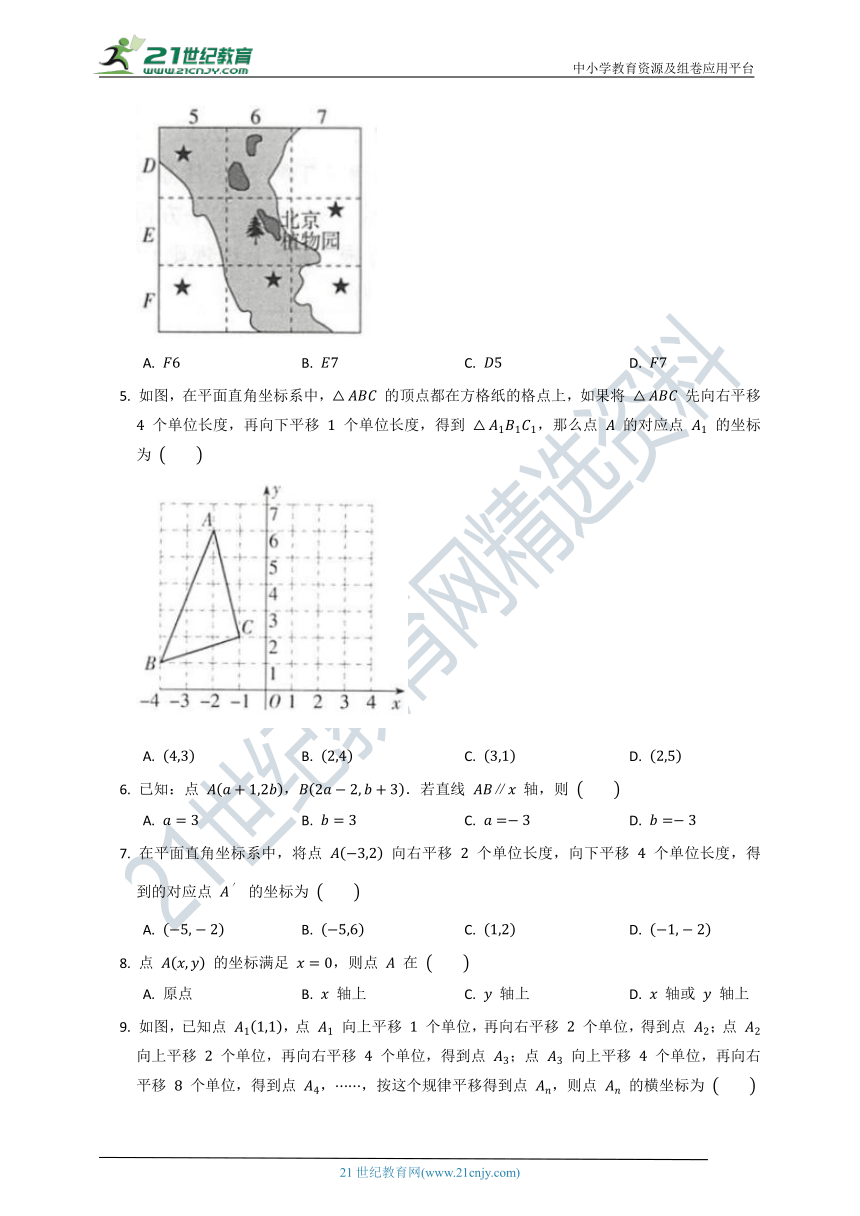
4. 共享单车方便了人们的出行,小白同学在北京植物园打开某共享单车 ,如图,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是
A. B. C. D.
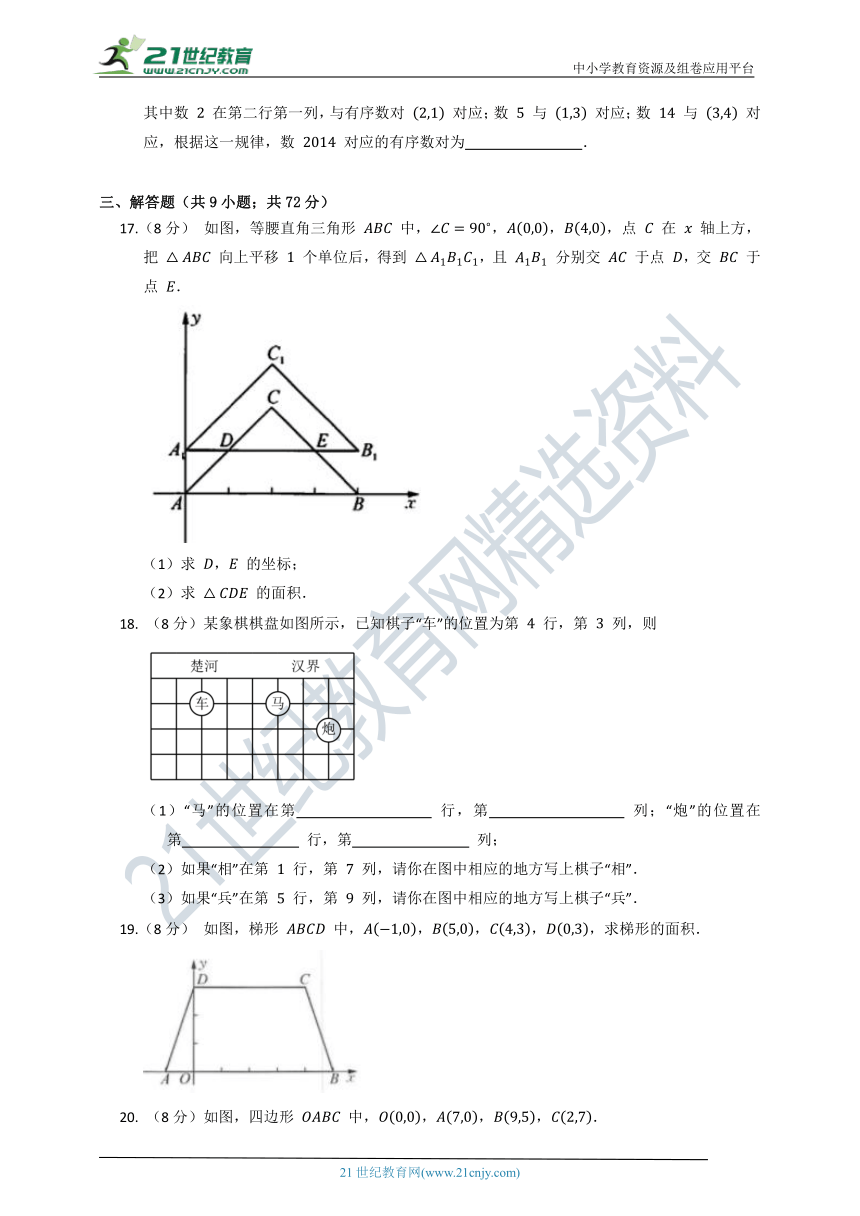
5. 如图,在平面直角坐标系中, 的顶点都在方格纸的格点上,如果将 先向右平移 个单位长度,再向下平移 个单位长度,得到 ,那么点 的对应点 的坐标为
A. B. C. D.
6. 已知:点 ,.若直线 轴,则
A. B. C. D.
7. 在平面直角坐标系中,将点 向右平移 个单位长度,向下平移 个单位长度,得到的对应点 的坐标为
A. B. C. D.
8. 点 的坐标满足 ,则点 在
A. 原点 B. 轴上 C. 轴上 D. 轴或 轴上
9. 如图,已知点 ,点 向上平移 个单位,再向右平移 个单位,得到点 ;点 向上平移 个单位,再向右平移 个单位,得到点 ;点 向上平移 个单位,再向右平移 个单位,得到点 ,,按这个规律平移得到点 ,则点 的横坐标为
A. B. C. D.
10. 已知点 ,,点 在 轴上,且 的面积为 ,则点 的坐标为
A. B.
C. 或 D. 无法确定
二、填空题(共6小题;每小题3分,共18分)
11. 已知线段 由线段 平移得到,点 的对应点为 ,那么点 的对应点点 的坐标为 .
12. 已知点 ,点 ,点 ,如果 的面积为 ,那么 的值为 .
13. 平面直角坐标系的两条坐标轴把平面分成四个区域,这四个区域依次叫做 , , , ,同时规定 轴、 轴 任何象限.
14. 点 向上平移 个单位后的对应点 的坐标是 ,它落在第 象限.
15. 如图所示的东莞地图,若在图中建立平面直角坐标系,使“虎门”的坐标是 ,则“东城”的坐标为 .
16. 将正整数按如图所示的规律排列:
其中数 在第二行第一列,与有序数对 对应;数 与 对应;数 与 对应,根据这一规律,数 对应的有序数对为 .
三、解答题(共9小题;共72分)
17.(8分) 如图,等腰直角三角形 中,,,,点 在 轴上方,把 向上平移 个单位后,得到 ,且 分别交 于点 ,交 于点 .
(1)求 , 的坐标;
(2)求 的面积.
18. (8分)某象棋棋盘如图所示,已知棋子“车”的位置为第 行,第 列,则
(1)“马”的位置在第 行,第 列;“炮”的位置在第 行,第 列;
(2)如果“相”在第 行,第 列,请你在图中相应的地方写上棋子“相”.
(3)如果“兵”在第 行,第 列,请你在图中相应的地方写上棋子“兵”.
19.(8分) 如图,梯形 中,,,,,求梯形的面积.
20. (8分)如图,四边形 中,,,,.
(1)求此四边形面积;
(2)在 轴上能否找到一点 ,使 面积等于 若有,求出点 的坐标,若没有,请说明理由.
21.(8分) 如图,已知 ,,,,求四边形 的面积.
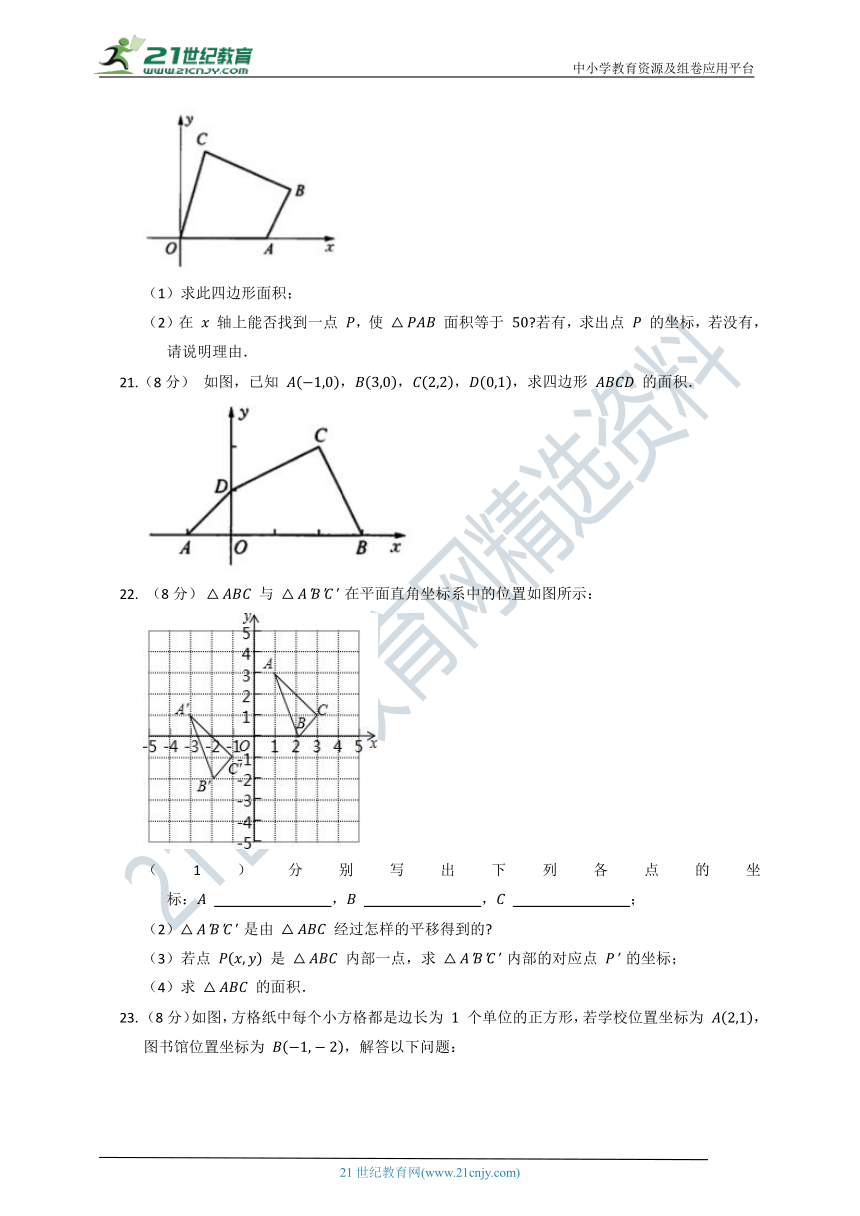
22. 与 在平面直角坐标系中的位置如图所示:
(1)分别写出下列各点的坐标: , , ;
(2) 是由 经过怎样的平移得到的
(3)若点 是 内部一点,求 内部的对应点 的坐标;
(4)求 的面积.
23. (8分)如图,方格纸中每个小方格都是边长为 个单位的正方形,若学校位置坐标为 ,图书馆位置坐标为 ,解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为 ,请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到,求的面积.
24.(8分) 如图,在平面直角坐标系中,对正方形 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘同一个实数 ,将得到的点先向右平移 个单位,再向上平移 个单位(,),得到正方形 及其内部的点,其中点 , 的对应点分别为点 ,,已知正方形 内部的一个点 经过上述操作后得到的对应点 与点 重合,求点 的坐标.
25.(8分) 如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 .
(1)观察每次变换前后的三角形的变化规律,若将 变换成 ,则 的坐标是 , 的坐标是 .
(2)若按第()题找到的规律将 进行 次变换,得到 ,比较每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是 .
答案
一
1. B
2. B
3. A
4. A
【解析】观察题图可知,离小白最近的是 ,故选A.
5. D
【解析】由题图可得 ,将 先向右平移 个单位长度,再向下平移 个单位长度,则点 的对应点 的坐标为 ,即 ,故选D.
6. B
7. D
8. C
9. C
【解析】由题意知,点 的横坐标为 ,点 的横坐标为 ,点 的横坐标为 ,点 的横坐标为 ,,按这个规律平移得到点 ,则点 的横坐标为 .
10. C
【解析】,,点 在 轴上,
边上的高为 ,
又 的面积为 ,
,
易知点 在点 的左边或者右边,
点 的坐标为 或 .
故选C.
二
11.
12. 或
13. 第一象限,第二象限,第三象限,第四象限,不属于
14. ,一
15.
16.
【解析】观察:
可发现:第奇数行第一列的数等于该行行数的平方,第偶数列的第一行等于该列列数的平方.
因为 ,第 行前 列的数向右依次减小,
又 ,
所以数 在第 行第 列,即数 对应的有序数对为 .
三
17. (1) ,.
(2) .
18. (1) ;;;;
(2) 所作图形如下:
(3) 所作图形如下:
19. .
20. (1) .
(2) 或 (提示:设 ,解 得 ).
21. .
22. (1) ;;
(2) 先向左平移 个单位,再向下平移 个单位;
或:先向下平移 个单位,再向左平移 个单位.
(3) 由题意可得:.
(4)
23. (1) 如图,点 即为原点.
(2) 如图,点 即为所求.
(3)
24. 设 ,
由题意得
解得
因为点 与点 重合,
所以 ,
则
解得
所以 .
25. (1) ;
(2) ;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2022-2023学年七年级(下)第七章平面直角坐标系检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 直角坐标平面上的点 通过上下平移不能与之重合的是
A. B. C. D.
2. 对于任何实数 ,点 一定不在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、 正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是
A. 滑雪大跳台 B. 五一剧场
C. 冬奥组委会 D. 全民畅读艺术书店
4. 共享单车方便了人们的出行,小白同学在北京植物园打开某共享单车 ,如图,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是
A. B. C. D.
5. 如图,在平面直角坐标系中, 的顶点都在方格纸的格点上,如果将 先向右平移 个单位长度,再向下平移 个单位长度,得到 ,那么点 的对应点 的坐标为
A. B. C. D.
6. 已知:点 ,.若直线 轴,则
A. B. C. D.
7. 在平面直角坐标系中,将点 向右平移 个单位长度,向下平移 个单位长度,得到的对应点 的坐标为
A. B. C. D.
8. 点 的坐标满足 ,则点 在
A. 原点 B. 轴上 C. 轴上 D. 轴或 轴上
9. 如图,已知点 ,点 向上平移 个单位,再向右平移 个单位,得到点 ;点 向上平移 个单位,再向右平移 个单位,得到点 ;点 向上平移 个单位,再向右平移 个单位,得到点 ,,按这个规律平移得到点 ,则点 的横坐标为
A. B. C. D.
10. 已知点 ,,点 在 轴上,且 的面积为 ,则点 的坐标为
A. B.
C. 或 D. 无法确定
二、填空题(共6小题;每小题3分,共18分)
11. 已知线段 由线段 平移得到,点 的对应点为 ,那么点 的对应点点 的坐标为 .
12. 已知点 ,点 ,点 ,如果 的面积为 ,那么 的值为 .
13. 平面直角坐标系的两条坐标轴把平面分成四个区域,这四个区域依次叫做 , , , ,同时规定 轴、 轴 任何象限.
14. 点 向上平移 个单位后的对应点 的坐标是 ,它落在第 象限.
15. 如图所示的东莞地图,若在图中建立平面直角坐标系,使“虎门”的坐标是 ,则“东城”的坐标为 .
16. 将正整数按如图所示的规律排列:
其中数 在第二行第一列,与有序数对 对应;数 与 对应;数 与 对应,根据这一规律,数 对应的有序数对为 .
三、解答题(共9小题;共72分)
17.(8分) 如图,等腰直角三角形 中,,,,点 在 轴上方,把 向上平移 个单位后,得到 ,且 分别交 于点 ,交 于点 .
(1)求 , 的坐标;
(2)求 的面积.
18. (8分)某象棋棋盘如图所示,已知棋子“车”的位置为第 行,第 列,则
(1)“马”的位置在第 行,第 列;“炮”的位置在第 行,第 列;
(2)如果“相”在第 行,第 列,请你在图中相应的地方写上棋子“相”.
(3)如果“兵”在第 行,第 列,请你在图中相应的地方写上棋子“兵”.
19.(8分) 如图,梯形 中,,,,,求梯形的面积.
20. (8分)如图,四边形 中,,,,.
(1)求此四边形面积;
(2)在 轴上能否找到一点 ,使 面积等于 若有,求出点 的坐标,若没有,请说明理由.
21.(8分) 如图,已知 ,,,,求四边形 的面积.
22. 与 在平面直角坐标系中的位置如图所示:
(1)分别写出下列各点的坐标: , , ;
(2) 是由 经过怎样的平移得到的
(3)若点 是 内部一点,求 内部的对应点 的坐标;
(4)求 的面积.
23. (8分)如图,方格纸中每个小方格都是边长为 个单位的正方形,若学校位置坐标为 ,图书馆位置坐标为 ,解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为 ,请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到,求的面积.
24.(8分) 如图,在平面直角坐标系中,对正方形 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘同一个实数 ,将得到的点先向右平移 个单位,再向上平移 个单位(,),得到正方形 及其内部的点,其中点 , 的对应点分别为点 ,,已知正方形 内部的一个点 经过上述操作后得到的对应点 与点 重合,求点 的坐标.
25.(8分) 如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 .
(1)观察每次变换前后的三角形的变化规律,若将 变换成 ,则 的坐标是 , 的坐标是 .
(2)若按第()题找到的规律将 进行 次变换,得到 ,比较每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是 .
答案
一
1. B
2. B
3. A
4. A
【解析】观察题图可知,离小白最近的是 ,故选A.
5. D
【解析】由题图可得 ,将 先向右平移 个单位长度,再向下平移 个单位长度,则点 的对应点 的坐标为 ,即 ,故选D.
6. B
7. D
8. C
9. C
【解析】由题意知,点 的横坐标为 ,点 的横坐标为 ,点 的横坐标为 ,点 的横坐标为 ,,按这个规律平移得到点 ,则点 的横坐标为 .
10. C
【解析】,,点 在 轴上,
边上的高为 ,
又 的面积为 ,
,
易知点 在点 的左边或者右边,
点 的坐标为 或 .
故选C.
二
11.
12. 或
13. 第一象限,第二象限,第三象限,第四象限,不属于
14. ,一
15.
16.
【解析】观察:
可发现:第奇数行第一列的数等于该行行数的平方,第偶数列的第一行等于该列列数的平方.
因为 ,第 行前 列的数向右依次减小,
又 ,
所以数 在第 行第 列,即数 对应的有序数对为 .
三
17. (1) ,.
(2) .
18. (1) ;;;;
(2) 所作图形如下:
(3) 所作图形如下:
19. .
20. (1) .
(2) 或 (提示:设 ,解 得 ).
21. .
22. (1) ;;
(2) 先向左平移 个单位,再向下平移 个单位;
或:先向下平移 个单位,再向左平移 个单位.
(3) 由题意可得:.
(4)
23. (1) 如图,点 即为原点.
(2) 如图,点 即为所求.
(3)
24. 设 ,
由题意得
解得
因为点 与点 重合,
所以 ,
则
解得
所以 .
25. (1) ;
(2) ;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
