7.4 专题 “双星”和“多星”问题 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共12张PPT)
文档属性
| 名称 | 7.4 专题 “双星”和“多星”问题 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1010.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-22 20:36:28 | ||
图片预览




文档简介
(共12张PPT)
“双星”和“多星”问题
m1
m2
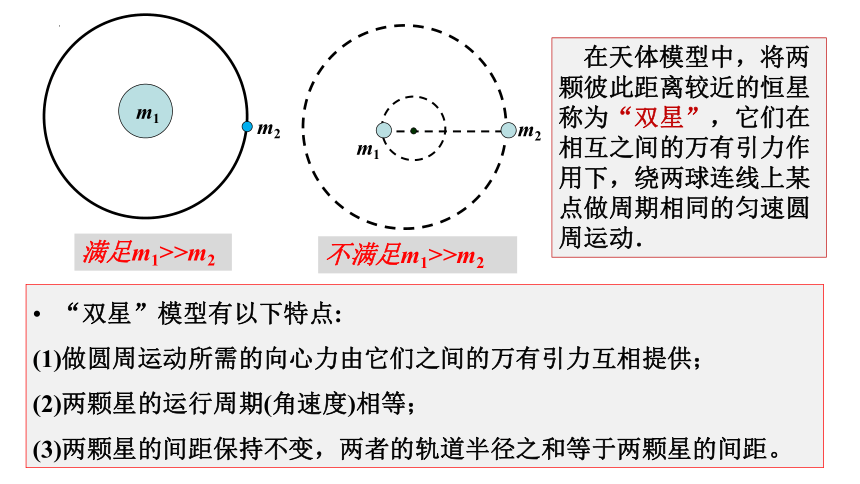
满足m1>>m2
m1
m2
不满足m1>>m2
在天体模型中,将两颗彼此距离较近的恒星称为“双星”,它们在相互之间的万有引力作用下,绕两球连线上某点做周期相同的匀速圆周运动.
“双星”模型有以下特点:
(1)做圆周运动所需的向心力由它们之间的万有引力互相提供;
(2)两颗星的运行周期(角速度)相等;
(3)两颗星的间距保持不变,两者的轨道半径之和等于两颗星的间距。
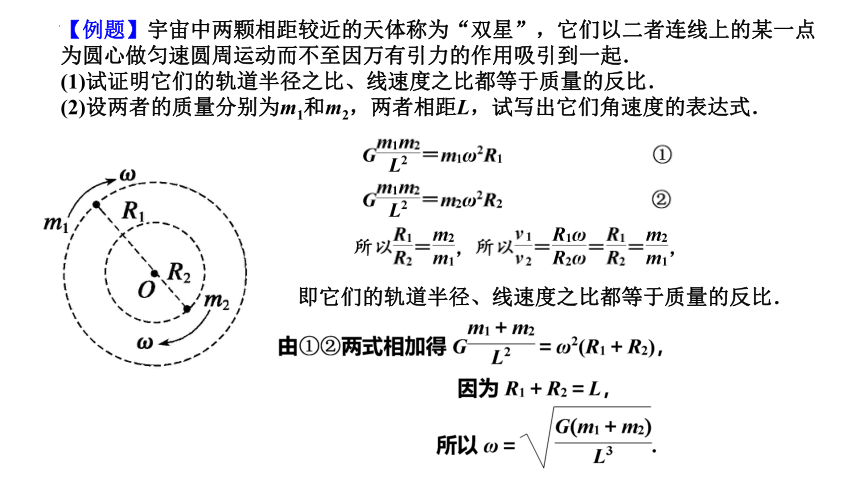
【例题】宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动而不至因万有引力的作用吸引到一起.
(1)试证明它们的轨道半径之比、线速度之比都等于质量的反比.
(2)设两者的质量分别为m1和m2,两者相距L,试写出它们角速度的表达式.
即它们的轨道半径、线速度之比都等于质量的反比.
1.(2012重庆)冥王星与其附近的星体卡戎可视为双星系统,质量比约为7:1,同时绕它们连线上某点O做匀速圆周运动。由此可知冥王星绕O点运动的( )
A.轨道半径约为卡戎的1/7
B.角速度大小约为卡戎的1/7
C.线度大小约为卡戎的7倍
D.向心力大小约为卡戎的7倍
2.月球与地球质量之比约为1∶80,有研究者认为月球和地球可视为一个由两质点构成的双星系统,它们都围绕月地连线上某点O做匀速圆周运动.据此观点,可知月球与地球绕O点运动的线速度大小之比约为( ).
A.1∶6 400 B.1∶80 C.80∶1 D.6 400∶1
3.(2018全国1)2017年,人类第一次直接探测到来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈,将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
4.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,双星之间的距离变为原来的n倍,则此时圆周运动的周期为 。
“三星”模型 “四星”模型
由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式,三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动,图为A、B、C三颗星体质量不相同时的一般情况。
5.如图所示,A、B、C三颗行星组成一个独立的三星系统,在相互的万有引力作用下,绕一个共同的圆心O做角速度相等的圆周运动,已知A、B两星的质量均为m,C星的质量为2m,等边三角形的每边长为L,则( )
x
y
Fx合
Fy合
(1)运动天体的向心力由其他天体的万有引力的合力提供;
方法概述
解决此类双星、三星、四星等多星天体的运动问题,要注意:
(2)运动天体的角速度相等;
(3)天体运动的轨道半径不是天体间的距离,要利用几何知识,寻找两者之间的关系。
“双星”和“多星”问题
m1
m2
满足m1>>m2
m1
m2
不满足m1>>m2
在天体模型中,将两颗彼此距离较近的恒星称为“双星”,它们在相互之间的万有引力作用下,绕两球连线上某点做周期相同的匀速圆周运动.
“双星”模型有以下特点:
(1)做圆周运动所需的向心力由它们之间的万有引力互相提供;
(2)两颗星的运行周期(角速度)相等;
(3)两颗星的间距保持不变,两者的轨道半径之和等于两颗星的间距。
【例题】宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动而不至因万有引力的作用吸引到一起.
(1)试证明它们的轨道半径之比、线速度之比都等于质量的反比.
(2)设两者的质量分别为m1和m2,两者相距L,试写出它们角速度的表达式.
即它们的轨道半径、线速度之比都等于质量的反比.
1.(2012重庆)冥王星与其附近的星体卡戎可视为双星系统,质量比约为7:1,同时绕它们连线上某点O做匀速圆周运动。由此可知冥王星绕O点运动的( )
A.轨道半径约为卡戎的1/7
B.角速度大小约为卡戎的1/7
C.线度大小约为卡戎的7倍
D.向心力大小约为卡戎的7倍
2.月球与地球质量之比约为1∶80,有研究者认为月球和地球可视为一个由两质点构成的双星系统,它们都围绕月地连线上某点O做匀速圆周运动.据此观点,可知月球与地球绕O点运动的线速度大小之比约为( ).
A.1∶6 400 B.1∶80 C.80∶1 D.6 400∶1
3.(2018全国1)2017年,人类第一次直接探测到来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈,将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
4.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,双星之间的距离变为原来的n倍,则此时圆周运动的周期为 。
“三星”模型 “四星”模型
由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式,三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动,图为A、B、C三颗星体质量不相同时的一般情况。
5.如图所示,A、B、C三颗行星组成一个独立的三星系统,在相互的万有引力作用下,绕一个共同的圆心O做角速度相等的圆周运动,已知A、B两星的质量均为m,C星的质量为2m,等边三角形的每边长为L,则( )
x
y
Fx合
Fy合
(1)运动天体的向心力由其他天体的万有引力的合力提供;
方法概述
解决此类双星、三星、四星等多星天体的运动问题,要注意:
(2)运动天体的角速度相等;
(3)天体运动的轨道半径不是天体间的距离,要利用几何知识,寻找两者之间的关系。
