人教版数学八年级下册18.2.1 矩形 同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.2.1 矩形 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 21:47:57 | ||
图片预览



文档简介
18.2.1 矩形 同步练习
一、单选题
1.在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为( )
A.1 B.2 C.1.5 D.
2.直角三角形的两条直角边长为3和4,则它斜边上的中线长为( )
A.5 B.2 C.2.5 D.1.5
3.关于矩形的性质,以下说法不正确的是( )
A.对边平行且相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
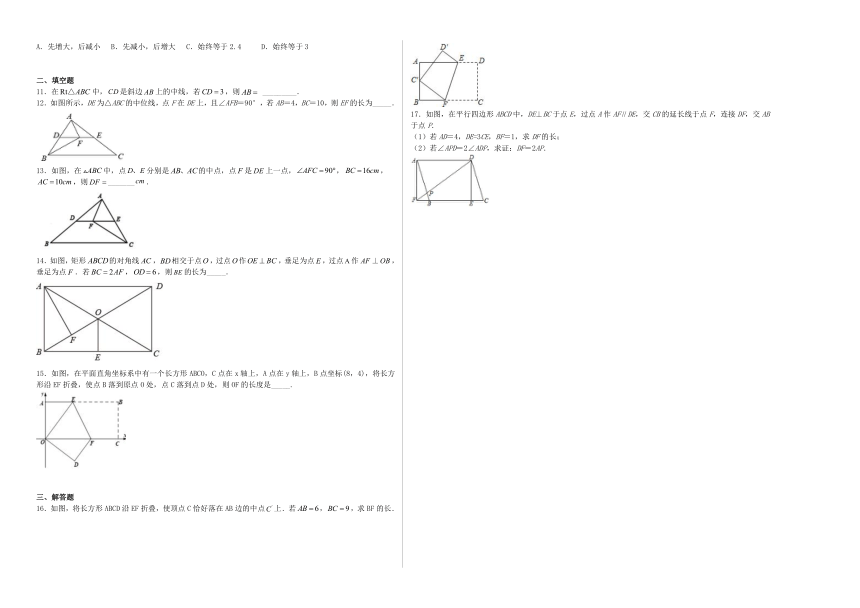
4.如图,在中,平分交于点为的中点,连结,则的周长是( )
A.23 B.25 C. D.22
5.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
A. B. C.3 D.4
6.如图,矩形的对角线,交于点,且,以为斜边作等腰直角三角形,连接,则的度数为( )
A. B. C. D.
7.如图,矩形的边,E为上一点,且,F为边上的一个动点,连接,若以为边向右侧作等腰直角三角形,连接,则的最小值为( )
A. B. C.3 D.
8.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①AE=AD;②∠AED=∠CED;③BH=HF;④CF=DF;⑤BC﹣CF=2HE,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
9.如图,在平面直角坐标系中,矩形的边在轴上,顶点, ,连接,按下列方法作图:
(1)以点为圆心,适当长为半径画弧,分别交、于点,;
(2)分别以点,为圆心,大于的长为半径画弧两弧交于点;
(3)作射线交于点,则点的横坐标为( )
A. B. C.1 D.
10.如图,矩形ABCD的对角线AC、BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F,已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是( )
A.先增大,后减小 B.先减小,后增大 C.始终等于2.4 D.始终等于3
二、填空题
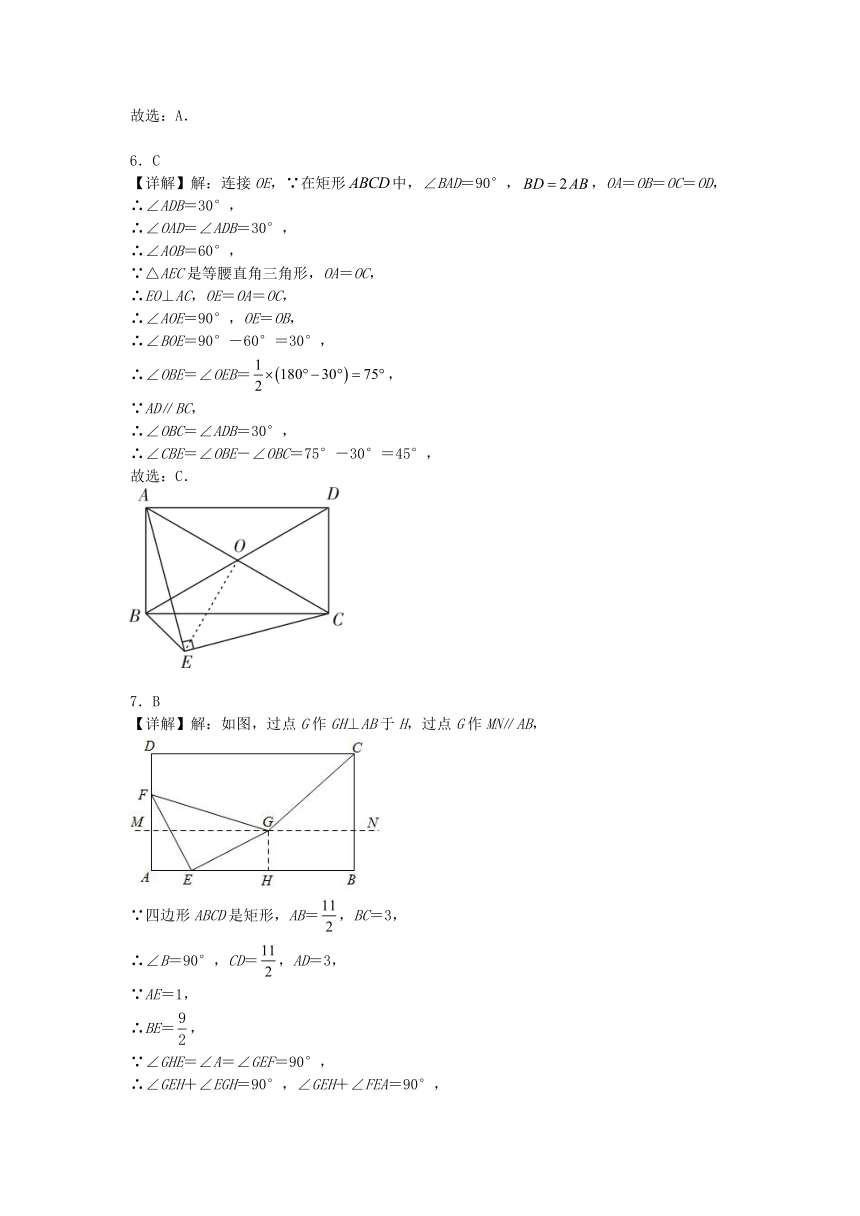
11.在中,是斜边上的中线,若,则 _________.
12.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为_____.
13.如图,在中,点分别是的中点,点是上一点,,,,则_______.
14.如图,矩形的对角线,相交于点,过点作,垂足为点,过点作,垂足为点.若,,则的长为_____.
15.如图,在平面直角坐标系中有一个长方形ABCO,C点在x轴上,A点在y轴上,B点坐标(8,4),将长方形沿EF折叠,使点B落到原点O处,点C落到点D处,则OF的长度是_____.
三、解答题
16.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.若,,求BF的长.
17.如图,在平行四边形ABCD中,DE⊥BC于点E,过点A作AFDE,交CB的延长线于点F,连接DF,交AB于点P.
(1)若AD=4,DE=3CE,BF=1,求DF的长;
(2)若∠APD=2∠ADP,求证:DF=2AP.
参考答案
1.A
【详解】∵∠ACB=90°,∠A=30°,BC=1,
∴AB=2BC=2×1=2,
∴AB边上的中线长= AB=.
故选A.
2.C
【详解】解:由勾股定理得,斜边=,
所以,斜边上中线长.
故选C.
3.C
【详解】矩形是特殊的平行四边形,矩形的对边平行且相等,对角线相等,是轴对称图形,故A,B,D选项正确,不符合题意,
对角线互相垂直是菱形的性质,故C不正确,符合题意.
故选C.
4.B
【详解】解:∵AB=AC,AE平分∠BAC交BC于点E,
∴BE=CE=5,AE⊥BC.
∴在直角△ABE中,由勾股定理知,AE==12,
又∵D为AB的中点,
∴DE=AD=AB=,
∴△ADE的周长=++12=25,
故选:B.
5.A
【详解】解:∵AB=12,BC=5,
∴AD=5,
∴BD==13,
根据折叠可得:AD=A′D=5,
∴A′B=13-5=8,
设AE=x,则A′E=x,BE=12-x,
在Rt△A′EB中:(12-x)2=x2+82,
解得:x=.
故选:A.
6.C
【详解】解:连接OE,∵在矩形中,∠BAD=90°,,OA=OB=OC=OD,
∴∠ADB=30°,
∴∠OAD=∠ADB=30°,
∴∠AOB=60°,
∵△AEC是等腰直角三角形,OA=OC,
∴EO⊥AC,OE=OA=OC,
∴∠AOE=90°,OE=OB,
∴∠BOE=90°-60°=30°,
∴∠OBE=∠OEB=,
∵AD∥BC,
∴∠OBC=∠ADB=30°,
∴∠CBE=∠OBE-∠OBC=75°-30°=45°,
故选:C.
7.B
【详解】解:如图,过点G作GH⊥AB于H,过点G作MN∥AB,
∵四边形ABCD是矩形,AB=,BC=3,
∴∠B=90°,CD=,AD=3,
∵AE=1,
∴BE=,
∵∠GHE=∠A=∠GEF=90°,
∴∠GEH+∠EGH=90°,∠GEH+∠FEA=90°,
∴∠EGH=∠FEA,
又∵GE=EF,
∴△GEH≌△EFA(AAS),
∴GH=AE=1,
∴点G在平行AB且到AB距离为1的直线MN上运动,
∴当F与D重合时,CG有最小值,此时AF=EH=3,
∴CG的最小值=,
故选B.
8.A
【详解】解:①设AB=a,则AD=,
∵AE平分∠BAD,
∴∠BAE=45°,
∴BA=BE.
∴在Rt△ABE中,AB=BE=a,
∴AE=,
∴AE=AD,故①正确;
②∵DH⊥AH,∠DAE=45°,AD=,
∴DH=AH=a,
∴DH=DC,
∴ED平分∠AEC,
∴∠AED=∠CED,故②正确;
③∵AH=AB=a,
∴∠ABH=∠AHB,
∵AB∥CD,
∴∠ABF+∠DFB=180°,
又∠AHB+∠BHE=180°,
∴∠BHE=∠HFD,
在△DHF和△EBH中,,
∴△DHF≌△EBH(AAS),
∴BH=HF,故③正确;
④∵△BHE≌△HFD,
∴HE=DF,
∵HE=AE AH=,
∴DF=,
∵CD=a,
∴CF=,
∴CF=DF,故④正确;
⑤∵BC=AD=,CF=,HE=,
∴BC CF=,
∴BC﹣CF=2HE,故⑤正确;
故选:A.
9.A
【详解】解:过点作于,如图,
由作法得平分,
,
矩形的顶点的坐标为, 点坐标为,
,,
在中,,
在和中,
,
∴,
,
,
设,则,,
在中,,
解得,
即,
点的横坐标为.
故选:A.
10.C
【详解】解:连接PO,如下图:
∵在矩形ABCD中,AB=3,AD=4,
∴,
,,,
,
∴,
,
,
∴;
故选C.
11.
【详解】解:∵是中的斜边,是斜边上的中线,
∴,
故答案为:6.
12.
【详解】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=2,
∴EF=DE﹣DF=3.
故答案为3.
13.
【详解】解:∵点分别是的中点,
∴DE是△ABC的中位线,
∴DE=,
又∵,,
∴,
∴DF=DE-EF=8-5=3cm
故答案为:3.
14.
【详解】解:∵在矩形中,
∴AO=CO=BO=DO=6,
∵,
∴BC=2BE,
∵,
∴BE=AF,
∵∠OBE+∠ABF=∠ABF+∠BAF =90°,
∴∠OBE=∠BAF,
∵
又∵∠AFB=∠BEO=90°,
∴,
∴AB=BO,
∴AB=BO=AO,
∴是等边三角形,
∴∠ABO=60°,
∴∠OBE=30°,
∴OE=3 ,,
故答案是:.
15.
【详解】连接,如图所示:
设
根据翻折原理可得:
∵B点坐标(8,4)
∴
∴
∵长方形ABCO
∴
∴
∴
解得:,即
∴OF的长度是
故填:5.
16.
【详解】解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC'=AB=3,CF=C'F
在Rt△BC'F中,C'F2=BF2+C'B2,
∴CF2=(9-CF)2+9
∴CF=5
∴BF=4.
17.
【详解】(1)∵四边形ABCD是平行四边形
∴ADBC,AD=BC
∵AFDE
∴四边形ADEF是平行四边形
∴AD=EF
∴BC=EF
∴BF=CE
∵BF=1
∴CE=1
∵DE=3CE
∴DE=3
∵DE⊥BC
∴在Rt△DEF中 =+=9+16=25
∴DF=5
(2)证明:连接AE交DF于点O
∵四边形ADEF为平行四边形且DE⊥BC
∴四边形ADEF为矩形
∴AE=DF,AE与DF互相平分
∴AO=DO
∴∠ADO=∠DAO
在△AOD中,∠AOP是外角
∴∠AOP=∠ADP+∠DAO=2∠ADP
∵∠APD=2∠ADP
∴∠AOP=∠APD
∴AO=AP
∵DF=AE=2AO
∴DF=2AP.
一、单选题
1.在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为( )
A.1 B.2 C.1.5 D.
2.直角三角形的两条直角边长为3和4,则它斜边上的中线长为( )
A.5 B.2 C.2.5 D.1.5
3.关于矩形的性质,以下说法不正确的是( )
A.对边平行且相等 B.对角线相等 C.对角线互相垂直 D.是轴对称图形
4.如图,在中,平分交于点为的中点,连结,则的周长是( )
A.23 B.25 C. D.22
5.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
A. B. C.3 D.4
6.如图,矩形的对角线,交于点,且,以为斜边作等腰直角三角形,连接,则的度数为( )
A. B. C. D.
7.如图,矩形的边,E为上一点,且,F为边上的一个动点,连接,若以为边向右侧作等腰直角三角形,连接,则的最小值为( )
A. B. C.3 D.
8.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①AE=AD;②∠AED=∠CED;③BH=HF;④CF=DF;⑤BC﹣CF=2HE,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
9.如图,在平面直角坐标系中,矩形的边在轴上,顶点, ,连接,按下列方法作图:
(1)以点为圆心,适当长为半径画弧,分别交、于点,;
(2)分别以点,为圆心,大于的长为半径画弧两弧交于点;
(3)作射线交于点,则点的横坐标为( )
A. B. C.1 D.
10.如图,矩形ABCD的对角线AC、BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F,已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是( )
A.先增大,后减小 B.先减小,后增大 C.始终等于2.4 D.始终等于3
二、填空题
11.在中,是斜边上的中线,若,则 _________.
12.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为_____.
13.如图,在中,点分别是的中点,点是上一点,,,,则_______.
14.如图,矩形的对角线,相交于点,过点作,垂足为点,过点作,垂足为点.若,,则的长为_____.
15.如图,在平面直角坐标系中有一个长方形ABCO,C点在x轴上,A点在y轴上,B点坐标(8,4),将长方形沿EF折叠,使点B落到原点O处,点C落到点D处,则OF的长度是_____.
三、解答题
16.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.若,,求BF的长.
17.如图,在平行四边形ABCD中,DE⊥BC于点E,过点A作AFDE,交CB的延长线于点F,连接DF,交AB于点P.
(1)若AD=4,DE=3CE,BF=1,求DF的长;
(2)若∠APD=2∠ADP,求证:DF=2AP.
参考答案
1.A
【详解】∵∠ACB=90°,∠A=30°,BC=1,
∴AB=2BC=2×1=2,
∴AB边上的中线长= AB=.
故选A.
2.C
【详解】解:由勾股定理得,斜边=,
所以,斜边上中线长.
故选C.
3.C
【详解】矩形是特殊的平行四边形,矩形的对边平行且相等,对角线相等,是轴对称图形,故A,B,D选项正确,不符合题意,
对角线互相垂直是菱形的性质,故C不正确,符合题意.
故选C.
4.B
【详解】解:∵AB=AC,AE平分∠BAC交BC于点E,
∴BE=CE=5,AE⊥BC.
∴在直角△ABE中,由勾股定理知,AE==12,
又∵D为AB的中点,
∴DE=AD=AB=,
∴△ADE的周长=++12=25,
故选:B.
5.A
【详解】解:∵AB=12,BC=5,
∴AD=5,
∴BD==13,
根据折叠可得:AD=A′D=5,
∴A′B=13-5=8,
设AE=x,则A′E=x,BE=12-x,
在Rt△A′EB中:(12-x)2=x2+82,
解得:x=.
故选:A.
6.C
【详解】解:连接OE,∵在矩形中,∠BAD=90°,,OA=OB=OC=OD,
∴∠ADB=30°,
∴∠OAD=∠ADB=30°,
∴∠AOB=60°,
∵△AEC是等腰直角三角形,OA=OC,
∴EO⊥AC,OE=OA=OC,
∴∠AOE=90°,OE=OB,
∴∠BOE=90°-60°=30°,
∴∠OBE=∠OEB=,
∵AD∥BC,
∴∠OBC=∠ADB=30°,
∴∠CBE=∠OBE-∠OBC=75°-30°=45°,
故选:C.
7.B
【详解】解:如图,过点G作GH⊥AB于H,过点G作MN∥AB,
∵四边形ABCD是矩形,AB=,BC=3,
∴∠B=90°,CD=,AD=3,
∵AE=1,
∴BE=,
∵∠GHE=∠A=∠GEF=90°,
∴∠GEH+∠EGH=90°,∠GEH+∠FEA=90°,
∴∠EGH=∠FEA,
又∵GE=EF,
∴△GEH≌△EFA(AAS),
∴GH=AE=1,
∴点G在平行AB且到AB距离为1的直线MN上运动,
∴当F与D重合时,CG有最小值,此时AF=EH=3,
∴CG的最小值=,
故选B.
8.A
【详解】解:①设AB=a,则AD=,
∵AE平分∠BAD,
∴∠BAE=45°,
∴BA=BE.
∴在Rt△ABE中,AB=BE=a,
∴AE=,
∴AE=AD,故①正确;
②∵DH⊥AH,∠DAE=45°,AD=,
∴DH=AH=a,
∴DH=DC,
∴ED平分∠AEC,
∴∠AED=∠CED,故②正确;
③∵AH=AB=a,
∴∠ABH=∠AHB,
∵AB∥CD,
∴∠ABF+∠DFB=180°,
又∠AHB+∠BHE=180°,
∴∠BHE=∠HFD,
在△DHF和△EBH中,,
∴△DHF≌△EBH(AAS),
∴BH=HF,故③正确;
④∵△BHE≌△HFD,
∴HE=DF,
∵HE=AE AH=,
∴DF=,
∵CD=a,
∴CF=,
∴CF=DF,故④正确;
⑤∵BC=AD=,CF=,HE=,
∴BC CF=,
∴BC﹣CF=2HE,故⑤正确;
故选:A.
9.A
【详解】解:过点作于,如图,
由作法得平分,
,
矩形的顶点的坐标为, 点坐标为,
,,
在中,,
在和中,
,
∴,
,
,
设,则,,
在中,,
解得,
即,
点的横坐标为.
故选:A.
10.C
【详解】解:连接PO,如下图:
∵在矩形ABCD中,AB=3,AD=4,
∴,
,,,
,
∴,
,
,
∴;
故选C.
11.
【详解】解:∵是中的斜边,是斜边上的中线,
∴,
故答案为:6.
12.
【详解】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=2,
∴EF=DE﹣DF=3.
故答案为3.
13.
【详解】解:∵点分别是的中点,
∴DE是△ABC的中位线,
∴DE=,
又∵,,
∴,
∴DF=DE-EF=8-5=3cm
故答案为:3.
14.
【详解】解:∵在矩形中,
∴AO=CO=BO=DO=6,
∵,
∴BC=2BE,
∵,
∴BE=AF,
∵∠OBE+∠ABF=∠ABF+∠BAF =90°,
∴∠OBE=∠BAF,
∵
又∵∠AFB=∠BEO=90°,
∴,
∴AB=BO,
∴AB=BO=AO,
∴是等边三角形,
∴∠ABO=60°,
∴∠OBE=30°,
∴OE=3 ,,
故答案是:.
15.
【详解】连接,如图所示:
设
根据翻折原理可得:
∵B点坐标(8,4)
∴
∴
∵长方形ABCO
∴
∴
∴
解得:,即
∴OF的长度是
故填:5.
16.
【详解】解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC'=AB=3,CF=C'F
在Rt△BC'F中,C'F2=BF2+C'B2,
∴CF2=(9-CF)2+9
∴CF=5
∴BF=4.
17.
【详解】(1)∵四边形ABCD是平行四边形
∴ADBC,AD=BC
∵AFDE
∴四边形ADEF是平行四边形
∴AD=EF
∴BC=EF
∴BF=CE
∵BF=1
∴CE=1
∵DE=3CE
∴DE=3
∵DE⊥BC
∴在Rt△DEF中 =+=9+16=25
∴DF=5
(2)证明:连接AE交DF于点O
∵四边形ADEF为平行四边形且DE⊥BC
∴四边形ADEF为矩形
∴AE=DF,AE与DF互相平分
∴AO=DO
∴∠ADO=∠DAO
在△AOD中,∠AOP是外角
∴∠AOP=∠ADP+∠DAO=2∠ADP
∵∠APD=2∠ADP
∴∠AOP=∠APD
∴AO=AP
∵DF=AE=2AO
∴DF=2AP.
