人教版数学八年级下册18.2.3 正方形 同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.2.3 正方形 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 21:35:29 | ||
图片预览




文档简介
18.2.3 正方形 同步练习
一、单选题
1.七巧板是我国古代的一种拼板玩具,它已经有两千五百多年的历史了.如图所示的七巧板中,若平行四边形BEFG的周长等于10,则△BCD的周长等于( )
A.10 B.15 C.20 D.25
2.如图,三个边长均为4的正方形重叠在一起,,是其中两个正方形的对角线交点,则阴影部分面积是( )
A.2 B.4 C.6 D.8
3.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.由两个全等的三角形拼成的四边形是矩形
C.四个角都是直角的平行四边形是正方形
D.对角线相等且互相平分的四边形是矩形
4.下列说法正确的是( )
A.对角线相等的四边形是平行四边形 B.对角线互相垂直的四边形是正方形
C.矩形的对角线一定互相垂直 D.四条边相等的四边形是菱形
5.如图,在正方形中,是上任一点,,,点、分别是垂足,,则的值是( )
A. B. C. D.
6.如图所示,正方形的面积为9,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A.4.5 B.9 C.2.5 D.3
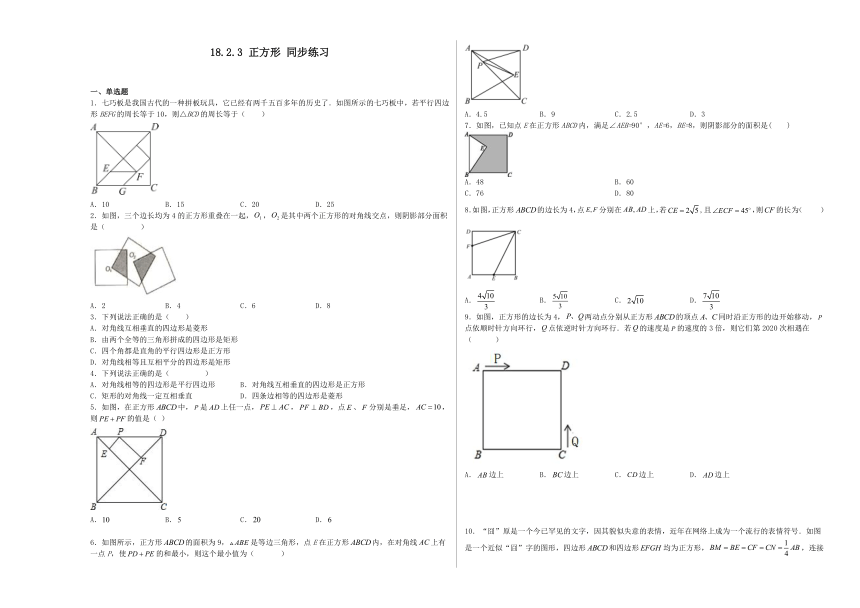
7.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
8.如图,正方形的边长为4,点分别在上,若,且,则的长为( )
A. B. C. D.
9.如图,正方形的边长为4,两动点分别从正方形的顶点同时沿正方形的边开始移动,点依顺时针方向环行,点依逆时针方向环行.若的速度是的速度的3倍,则它们第2020次相遇在( )
A.边上 B.边上 C.边上 D.边上
10.“囧”原是一个今已罕见的文字,因其貌似失意的表情,近年在网络上成为一个流行的表情符号.如图是一个近似“囧”字的图形,四边形和四边形均为正方形,,连接并延长,交的延长线于点P,则三角形的面积是正方形面积的( )
A. B. C. D.
二、填空题
11.边长为5的正方形的对角线长是_____________ .
12.如图,、分别是正方形边、的中点,分别以、为折痕,使点、点落在的点处,则是_______________三角形.
13.如图所示,在平面直角坐标系中有两个边长均为的正方形和正方形,边与边与轴重合,连接,点关于的对称点为点,连接,与边相交于点,则点的坐标是________.
14.正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为______.
15.如图 ,正方形 ABCD 中,AC 、BD 交于O ,EOF 90 ,已知 AE 3, CF 4 ,则 EF的长为_____.
三、解答题
16.如图,在四边形AECF中,.CE、CF分别是△ABC的内,外角平分线.
(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
17.如图,正方形ABCD的右侧作等边△ABE,连接DE、AC交于点F,连接BF,
(1)求证:
(2)求证:∠AFE=60°
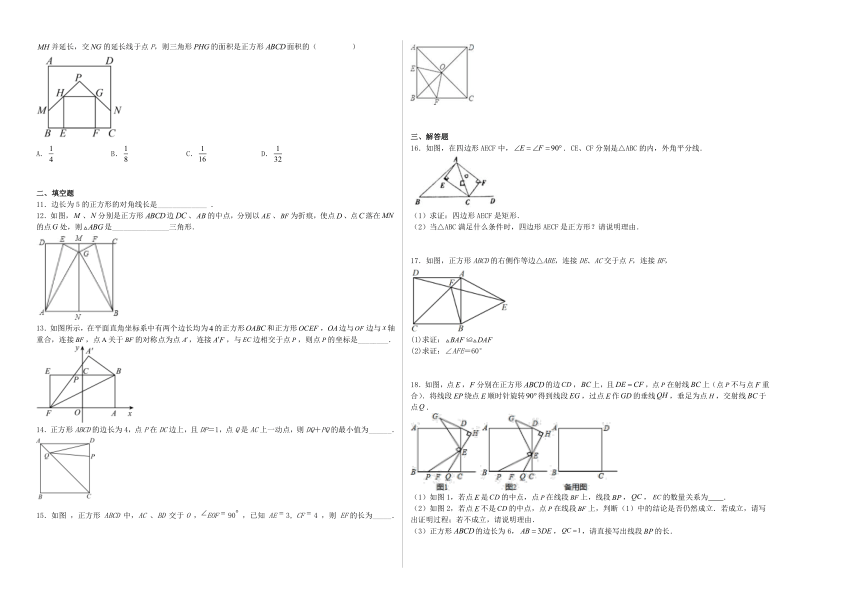
18.如图,点,分别在正方形的边,上,且,点在射线上(点不与点重合).将线段绕点顺时针旋转得到线段,过点作的垂线,垂足为点,交射线于点.
(1)如图1,若点是的中点,点在线段上,线段,,的数量关系为 .
(2)如图2,若点不是的中点,点在线段上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形的边长为6,,,请直接写出线段的长.
参考答案
1.C
【详解】解:∵平行四边形BGFE是七巧板中的平行四边形,
∴BC=2BG,BD=4BE,BC=CD,
∵平行四边形BEFG的周长等于10,
∴2(BE+BG)=10,
∴△BCD的周长=BC+CD+BD=2BG+2BG+4BE=4(BE+BG)=20,
故选:C.
2.D
【详解】连接O1B,O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中
,
∴△O1BF≌△O1CG(ASA),
∴O1、O2两个正方形阴影部分的面积是S正方形,
同理另外两个正方形阴影部分的面积也是S正方形,
∴S阴影=S正方形=8.
故选D.
3.D
【详解】解:A.对角线互相垂直平分的四边形是菱形,故A错误;
B.由两个全等的直角三角形拼成的四边形是矩形,故B错误;
C.四个角都是直角的菱形是正方形,故C错误;
D.对角线相等且互相平分的四边形是矩形,正确;
故选:D.
4.D
【详解】解:、对角线互相平分的四边形是平行四边形,故选项说法错误,不符合题意;
、对角线相等,互相垂直平分的四边形是正方形,故选项说法错误,不符合题意;
、矩形的对角线相等,故选项说法错误,不符合题意;
、四条边相等的四边形是菱形,说法正确,
故选:D.
5.B
【详解】解:如图所示:
∵四边形ABCD是正方形,
∴∠PAE=45°,OA=AC=5,AC⊥BD,
∴∠AOD=90°,
∵PE⊥AC,PF⊥BD,
∴∠PEA=∠PEO=∠PFO=90°,
∴四边形OEPF是矩形,△PAE是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA=5;
故选B.
6.D
【详解】解:设BE与交于点,连接,,
∵点B与D关于对称,
∴,
∴最小.
∵正方形的面积为9,
∴,
又∵是等边三角形,
∴.
故选:D
7.C
【详解】解:∵∠AEB=90°,AE=6,BE=8,
∴AB=
∴S阴影部分=S正方形ABCD-SRt△ABE=102-
=100-24
=76.
故选:C.
8.A
【详解】解: 正方形,
把绕点C逆时针旋转90°得,
此时E,B,三点共线,则,连接EF.
∴,
∵,∠ECF=45°,
∴
∵CE=CE,
∴(SAS),
∴.
在Rt中,
∴AE=AB-BE=2.
设DF=x,则AF=4-x.
∵
∴,
在Rt中,
∴
解得:.
在Rt中,
∴
解得:
故选:A.
9.A
【详解】正方形的边长为4,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
①第一次相遇甲乙行的路程和为8,甲行的路程为8×=2,乙行的路程为8 2=6,在AD边相遇;
②第二次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在DC边相遇;
③第三次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在CB边相遇;
④第四次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在AB边相遇;
…
∵2020=505×4,
∴甲、乙第2017次相遇在边AB上.
故选:A.
10.C
【详解】解:连接MN,MN分别交HE,GF于点L,K,如图,
设正方形ABCD的边长为a,
∵四边形ABCD为正方形,
∴∠B=∠C=90°,BM∥CN,
∵BM=CN,
∴四边形MBCN为矩形,
∴MN=BC=a.
∵四边形ABCD为正方形,BM=BE=CF=CN=AB=a,
∴四边形MBEL和四边形KFCN为正方形,
∴ML=LE=KF=KN=a.
∴EF=EH=HG=BC-BE-CF=a.
∴HL=HE-LE=a,
∴ML=HL,
∴△MHL为等腰直角三角形,
同理:△KNG为等腰直角三角形,
∴∠MHL=∠NGK=45°,
∵∠EHG=∠HGF=90°,
∴∠PHG=∠PGH=45°,
∴△PHG为等腰直角三角形,
∴PH=PG=HG=a,
∴S△PGH=×PH PG=a2,
∵S正方形ABCD=a2,
∴三角形PHG的面积是正方形ABCD面积的,
故选:C.
11.
【详解】如图所示:
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=5,AC=BD,
∴BD=AC===5.
12.
【详解】解:四边形是正方形,
AD=AB=BC,
以、为折痕,使点、点落在的点处,
AG=AD,BG=BC,
AG=AB=BG,
△ABG是等边三角形;
故答案为等边.
13.
【详解】解:∵正方形和正方形的边长为4,
∴EF=AB=BC=4, ,
∴ , ,
∵点关于的对称点为点,
∴ ,
∴,
∴ ,
设 ,则 , ,
在 中,由勾股定理得
,
解得: ,
∴PB=5,
∴PC=1,
∴点的坐标是(-1,4).
故答案为:.
14.
【详解】解:如图,连接BP,
由正方形ABCD的性质可知点B和点D关于直线AC对称,
∴QB=QD,
则BP就是DQ+PQ的最小值,
∵正方形ABCD的边长是4,DP=1,
∴CP=3,
∴BP=,
∴DQ+PQ的最小值是5.
故答案为5.
15.
【详解】解:如图所示,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵AC,BD为正方形的对角线,
∴∠OAE=∠OBF,OA=OB,
在△AOE和△BOF中,
,
△AOE≌△BOF,
∴AE=BF=3, 同理可证:△BOE≌△COF, 即CF=BE=4,
∴EF= =5. 故答案为5.
16.
【详解】(1)证明:∵CE、CF分别是的内、外角平分线,
,.
,即.
,
∴四边形AECF是矩形.
(2)解:当满足时,四边形AECF是正方形.
理由:
..
∵四边形AECF是矩形,∴四边形AECF是正方形.
故答案为(1)见解析;(2)当满足时,四边形AECF是正方形,见解析.
17.
(1)
证明:在正方形ABCD中,DA=BA,∠DAF=∠BAF=45°,
在△BAF与△DAF中,
∵,
∴(SAS);
(2)
∵△ABE是等边三角形,
∴AD=AB=AE,∠BAE=60°,
∴∠DAE=∠DAB+∠BAE=90°+60°=150°,
∴∠ADF=,
∵∠DAC=45°,
∴∠AFE=∠ADF+∠DAC=15°+45°=60°.
18.
【详解】(1);理由如下:
四边形是正方形,
,,
由旋转的性质得:,,
,
,
,,
,
又,,
,
在和中,,
,
,
,即;
故答案为;
(2)(1)中的结论仍然成立,理由如下:
由题意得:,,
,
,
,,
,
四边形是正方形,
,,
,
,
,
在和中,,
,
,
,即;
(3)分两种情况:
①当点在线段上时,点在线段上,
由(2)可知:,
,
,,
;
②当点在射线上时,点在线段的延长线上,如图3所示:
同(2)可得:,
,
,,
,
;
综上所述,线段的长为3或5.
一、单选题
1.七巧板是我国古代的一种拼板玩具,它已经有两千五百多年的历史了.如图所示的七巧板中,若平行四边形BEFG的周长等于10,则△BCD的周长等于( )
A.10 B.15 C.20 D.25
2.如图,三个边长均为4的正方形重叠在一起,,是其中两个正方形的对角线交点,则阴影部分面积是( )
A.2 B.4 C.6 D.8
3.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.由两个全等的三角形拼成的四边形是矩形
C.四个角都是直角的平行四边形是正方形
D.对角线相等且互相平分的四边形是矩形
4.下列说法正确的是( )
A.对角线相等的四边形是平行四边形 B.对角线互相垂直的四边形是正方形
C.矩形的对角线一定互相垂直 D.四条边相等的四边形是菱形
5.如图,在正方形中,是上任一点,,,点、分别是垂足,,则的值是( )
A. B. C. D.
6.如图所示,正方形的面积为9,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A.4.5 B.9 C.2.5 D.3
7.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
8.如图,正方形的边长为4,点分别在上,若,且,则的长为( )
A. B. C. D.
9.如图,正方形的边长为4,两动点分别从正方形的顶点同时沿正方形的边开始移动,点依顺时针方向环行,点依逆时针方向环行.若的速度是的速度的3倍,则它们第2020次相遇在( )
A.边上 B.边上 C.边上 D.边上
10.“囧”原是一个今已罕见的文字,因其貌似失意的表情,近年在网络上成为一个流行的表情符号.如图是一个近似“囧”字的图形,四边形和四边形均为正方形,,连接并延长,交的延长线于点P,则三角形的面积是正方形面积的( )
A. B. C. D.
二、填空题
11.边长为5的正方形的对角线长是_____________ .
12.如图,、分别是正方形边、的中点,分别以、为折痕,使点、点落在的点处,则是_______________三角形.
13.如图所示,在平面直角坐标系中有两个边长均为的正方形和正方形,边与边与轴重合,连接,点关于的对称点为点,连接,与边相交于点,则点的坐标是________.
14.正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为______.
15.如图 ,正方形 ABCD 中,AC 、BD 交于O ,EOF 90 ,已知 AE 3, CF 4 ,则 EF的长为_____.
三、解答题
16.如图,在四边形AECF中,.CE、CF分别是△ABC的内,外角平分线.
(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
17.如图,正方形ABCD的右侧作等边△ABE,连接DE、AC交于点F,连接BF,
(1)求证:
(2)求证:∠AFE=60°
18.如图,点,分别在正方形的边,上,且,点在射线上(点不与点重合).将线段绕点顺时针旋转得到线段,过点作的垂线,垂足为点,交射线于点.
(1)如图1,若点是的中点,点在线段上,线段,,的数量关系为 .
(2)如图2,若点不是的中点,点在线段上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形的边长为6,,,请直接写出线段的长.
参考答案
1.C
【详解】解:∵平行四边形BGFE是七巧板中的平行四边形,
∴BC=2BG,BD=4BE,BC=CD,
∵平行四边形BEFG的周长等于10,
∴2(BE+BG)=10,
∴△BCD的周长=BC+CD+BD=2BG+2BG+4BE=4(BE+BG)=20,
故选:C.
2.D
【详解】连接O1B,O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中
,
∴△O1BF≌△O1CG(ASA),
∴O1、O2两个正方形阴影部分的面积是S正方形,
同理另外两个正方形阴影部分的面积也是S正方形,
∴S阴影=S正方形=8.
故选D.
3.D
【详解】解:A.对角线互相垂直平分的四边形是菱形,故A错误;
B.由两个全等的直角三角形拼成的四边形是矩形,故B错误;
C.四个角都是直角的菱形是正方形,故C错误;
D.对角线相等且互相平分的四边形是矩形,正确;
故选:D.
4.D
【详解】解:、对角线互相平分的四边形是平行四边形,故选项说法错误,不符合题意;
、对角线相等,互相垂直平分的四边形是正方形,故选项说法错误,不符合题意;
、矩形的对角线相等,故选项说法错误,不符合题意;
、四条边相等的四边形是菱形,说法正确,
故选:D.
5.B
【详解】解:如图所示:
∵四边形ABCD是正方形,
∴∠PAE=45°,OA=AC=5,AC⊥BD,
∴∠AOD=90°,
∵PE⊥AC,PF⊥BD,
∴∠PEA=∠PEO=∠PFO=90°,
∴四边形OEPF是矩形,△PAE是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA=5;
故选B.
6.D
【详解】解:设BE与交于点,连接,,
∵点B与D关于对称,
∴,
∴最小.
∵正方形的面积为9,
∴,
又∵是等边三角形,
∴.
故选:D
7.C
【详解】解:∵∠AEB=90°,AE=6,BE=8,
∴AB=
∴S阴影部分=S正方形ABCD-SRt△ABE=102-
=100-24
=76.
故选:C.
8.A
【详解】解: 正方形,
把绕点C逆时针旋转90°得,
此时E,B,三点共线,则,连接EF.
∴,
∵,∠ECF=45°,
∴
∵CE=CE,
∴(SAS),
∴.
在Rt中,
∴AE=AB-BE=2.
设DF=x,则AF=4-x.
∵
∴,
在Rt中,
∴
解得:.
在Rt中,
∴
解得:
故选:A.
9.A
【详解】正方形的边长为4,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
①第一次相遇甲乙行的路程和为8,甲行的路程为8×=2,乙行的路程为8 2=6,在AD边相遇;
②第二次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在DC边相遇;
③第三次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在CB边相遇;
④第四次相遇甲乙行的路程和为16,甲行的路程为16×=4,乙行的路程为16 4=12,在AB边相遇;
…
∵2020=505×4,
∴甲、乙第2017次相遇在边AB上.
故选:A.
10.C
【详解】解:连接MN,MN分别交HE,GF于点L,K,如图,
设正方形ABCD的边长为a,
∵四边形ABCD为正方形,
∴∠B=∠C=90°,BM∥CN,
∵BM=CN,
∴四边形MBCN为矩形,
∴MN=BC=a.
∵四边形ABCD为正方形,BM=BE=CF=CN=AB=a,
∴四边形MBEL和四边形KFCN为正方形,
∴ML=LE=KF=KN=a.
∴EF=EH=HG=BC-BE-CF=a.
∴HL=HE-LE=a,
∴ML=HL,
∴△MHL为等腰直角三角形,
同理:△KNG为等腰直角三角形,
∴∠MHL=∠NGK=45°,
∵∠EHG=∠HGF=90°,
∴∠PHG=∠PGH=45°,
∴△PHG为等腰直角三角形,
∴PH=PG=HG=a,
∴S△PGH=×PH PG=a2,
∵S正方形ABCD=a2,
∴三角形PHG的面积是正方形ABCD面积的,
故选:C.
11.
【详解】如图所示:
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=5,AC=BD,
∴BD=AC===5.
12.
【详解】解:四边形是正方形,
AD=AB=BC,
以、为折痕,使点、点落在的点处,
AG=AD,BG=BC,
AG=AB=BG,
△ABG是等边三角形;
故答案为等边.
13.
【详解】解:∵正方形和正方形的边长为4,
∴EF=AB=BC=4, ,
∴ , ,
∵点关于的对称点为点,
∴ ,
∴,
∴ ,
设 ,则 , ,
在 中,由勾股定理得
,
解得: ,
∴PB=5,
∴PC=1,
∴点的坐标是(-1,4).
故答案为:.
14.
【详解】解:如图,连接BP,
由正方形ABCD的性质可知点B和点D关于直线AC对称,
∴QB=QD,
则BP就是DQ+PQ的最小值,
∵正方形ABCD的边长是4,DP=1,
∴CP=3,
∴BP=,
∴DQ+PQ的最小值是5.
故答案为5.
15.
【详解】解:如图所示,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵AC,BD为正方形的对角线,
∴∠OAE=∠OBF,OA=OB,
在△AOE和△BOF中,
,
△AOE≌△BOF,
∴AE=BF=3, 同理可证:△BOE≌△COF, 即CF=BE=4,
∴EF= =5. 故答案为5.
16.
【详解】(1)证明:∵CE、CF分别是的内、外角平分线,
,.
,即.
,
∴四边形AECF是矩形.
(2)解:当满足时,四边形AECF是正方形.
理由:
..
∵四边形AECF是矩形,∴四边形AECF是正方形.
故答案为(1)见解析;(2)当满足时,四边形AECF是正方形,见解析.
17.
(1)
证明:在正方形ABCD中,DA=BA,∠DAF=∠BAF=45°,
在△BAF与△DAF中,
∵,
∴(SAS);
(2)
∵△ABE是等边三角形,
∴AD=AB=AE,∠BAE=60°,
∴∠DAE=∠DAB+∠BAE=90°+60°=150°,
∴∠ADF=,
∵∠DAC=45°,
∴∠AFE=∠ADF+∠DAC=15°+45°=60°.
18.
【详解】(1);理由如下:
四边形是正方形,
,,
由旋转的性质得:,,
,
,
,,
,
又,,
,
在和中,,
,
,
,即;
故答案为;
(2)(1)中的结论仍然成立,理由如下:
由题意得:,,
,
,
,,
,
四边形是正方形,
,,
,
,
,
在和中,,
,
,
,即;
(3)分两种情况:
①当点在线段上时,点在线段上,
由(2)可知:,
,
,,
;
②当点在射线上时,点在线段的延长线上,如图3所示:
同(2)可得:,
,
,,
,
;
综上所述,线段的长为3或5.
