20.1.1 平均数的意义 课件(共27张PPT)
文档属性
| 名称 | 20.1.1 平均数的意义 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 07:38:25 | ||
图片预览






文档简介
(共27张PPT)
20.1.1 平均数的意义
华师大版 八年级 下册
教学目标
教学目标:1. 掌握平均数的概念,会求一组数据的平均数.
2.能用平均数解决实际生活中的问题.
教学重点:算术平均数的意义和计算方法.
教学难点:体会平均数在不同情境中的应用.
新知导入
情境引入
当你听到“小亮的学习成绩比王明的成绩更好”,“A篮球队队员比B队更年轻”等诸如此类的说法时,你思考过这些话的含义吗?你知道人们是如何作出这些判断的吗?
新知讲解
合作学习
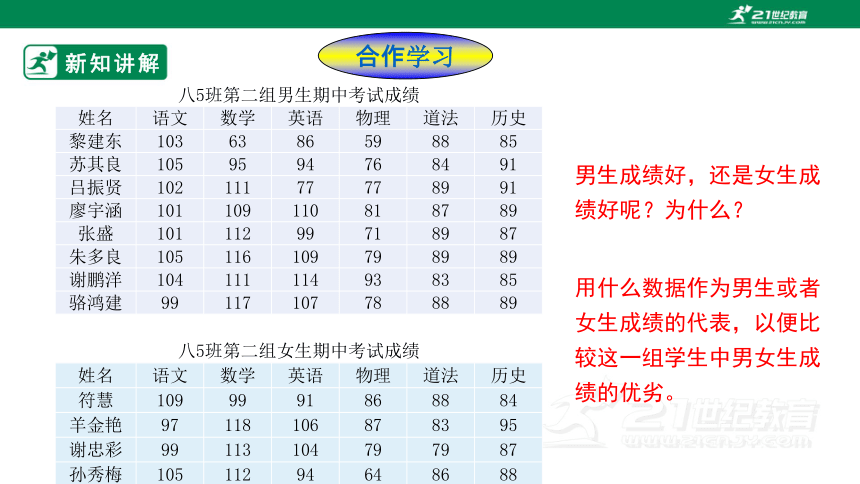
八5班第二组男生期中考试成绩 姓名 语文 数学 英语 物理 道法 历史
黎建东 103 63 86 59 88 85
苏其良 105 95 94 76 84 91
吕振贤 102 111 77 77 89 91
廖宇涵 101 109 110 81 87 89
张盛 101 112 99 71 89 87
朱多良 105 116 109 79 89 89
谢鹏洋 104 111 114 93 83 85
骆鸿建 99 117 107 78 88 89
八5班第二组女生期中考试成绩 姓名 语文 数学 英语 物理 道法 历史
符慧 109 99 91 86 88 84
羊金艳 97 118 106 87 83 95
谢忠彩 99 113 104 79 79 87
孙秀梅 105 112 94 64 86 88
男生成绩好,还是女生成绩好呢?为什么?
用什么数据作为男生或者女生成绩的代表,以便比较这一组学生中男女生成绩的优劣。
算一算:下表给出了某户居民 2010 年全年的水费缴纳情况(每两个月计费一次),请你帮这户居民算一算:平均每月缴纳多少水费?
某户居民 2010 年缴纳水费统计表
月份 2 4 6 8 10 12
水费(元) 50. 60 34. 60 41. 40 46. 00 39. 20 27. 60
平均每月水费=
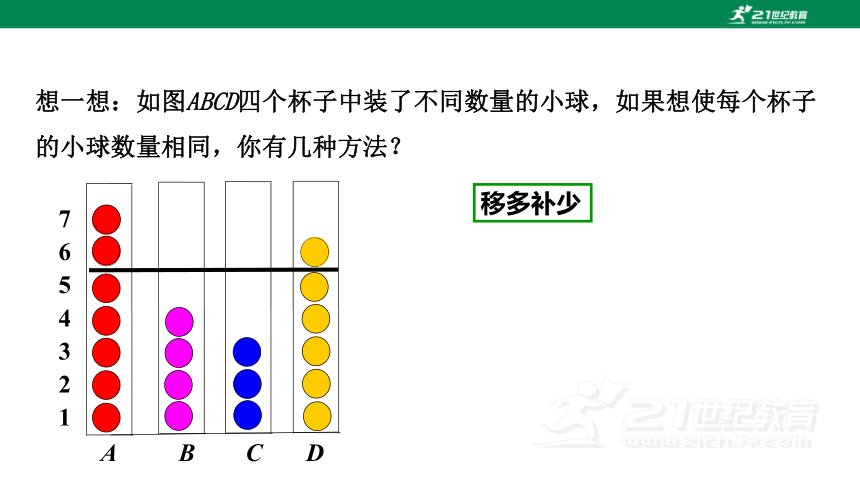
移多补少
想一想:如图ABCD四个杯子中装了不同数量的小球,如果想使每个杯子的小球数量相同,你有几种方法?
7
6
5
4
3
2
1
A B C D
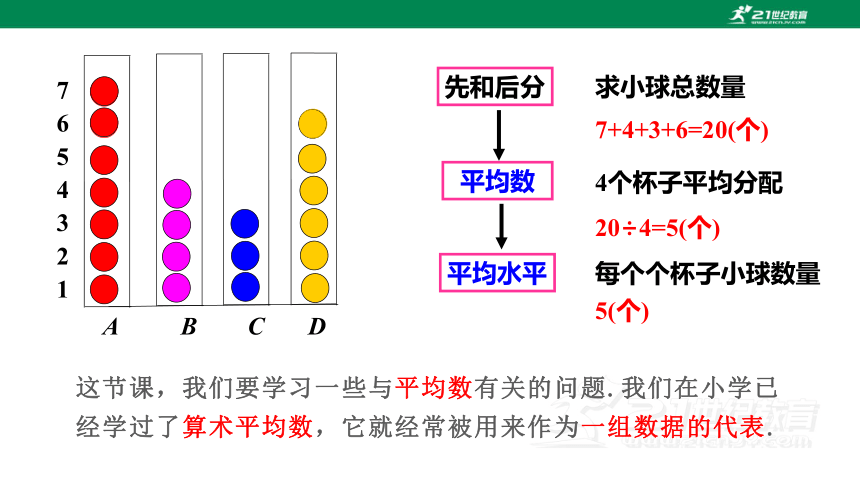
平均数
先和后分
平均水平
7
6
5
4
3
2
1
A B C D
求小球总数量
4个杯子平均分配
每个个杯子小球数量
7+4+3+6=20(个)
20÷4=5(个)
5(个)
这节课,我们要学习一些与平均数有关的问题.我们在小学已经学过了算术平均数,它就经常被用来作为一组数据的代表.
提炼概念
2.一般地,如果有 n 个数据 x1,x2,…,xn,我们把 表示这组数据的平均数,用“ ” 表示 ,即
1.日常生活中,我们常用平均数表示一组数据的“平均水平”.
典例精讲
例1 植树节到了,某单位组织职工开展植树竞赛,如图2反映的是植树量与人数之间的关系.
图1
图2
请根据图中信息计算:
(1) 总共有多少人参加了本次活动
(2) 总共植树多少棵
(3) 平均每人植树多少棵
解:参加本次活动的总人数是 1 + 8 + 1 +10 +8 + 3 + 1 = 32(人)
总共植树 3 × 8 + 4 × 1 + 5 × 10 + 6 × 8 + 7 ×3 + 8 × 1 =155(棵)
平均每人植树=
思考
你发现了植树总量、植树量的平均数和人数这三者之间的数量关系吗 你能解释“平均每人植树 4. 8 棵”的含义吗
植树总量=植树量的平均数×人数
平均每人植树 4. 8 棵意味着,有的人植树多于4.8棵,有的人植树少于4.8棵,多的人把多出4.8棵的部分给了少的人,最后每个人植树相同的棵数就是4.8棵.
例2 丁丁所在的八年级(1) 班共有学生 40 人.如图 是该校八年级各班学生人数分布情况
(1) 班
(2) 班
(3) 班
(4) 班
(5) 班
某校八年级各班学生人数分布图
利用扇形的大小来表示部分占总体的百分比大小的统计图叫做扇形统计图.
(1) 请计算该校八年级每班平均学生人数;
(2) 请计算各班学生人数,并绘制条形统计图
八年级(2) 班: 200 × 23% = 46(人);
八年级(3) 班: 200 × 20% = 40(人);
八年级(4) 班: 200 × 18% = 36(人);
八年级(5) 班: 200 × 19% = 38(人)
解:该校八年级学生总数为 40 ÷ 20% =200(人)
每班平均学生人数为 200 ÷ 5 = 40(人)
0
5
10
15
20
25
30
35
40
45
50
班级 初二1 初二2 初二3 初二4 初二5
人数 40 46 40 36 38
根据表格数据制作各班人数的条形统计图.
人
数
40
班级
1班
2班
3班
4班
5班
46
40
36
38
超出平均线的数量和
与
低于平均线的数量和
相 等
分析:先画坐标系,再画各个班级的条形图。
思考:左图中水平红色虚线代表平均人数40的水平线。想一想,水平线上方超出部分之和与下方不足部分之和在数量上有什么关系?
归纳概念
(1)一组数据的平均数是唯一的,它不一定是数据中的某个数据;
(2)平均数是反映数据集中趋势的一个统计量,是反映数据的平均水平(或中等水平)的一个特征量;
(3)一般情况下,平均数能体现一组数据的整体性质.
课堂练习
1.有m个数的平均数是x,n个数的平均数是y,则这(m+n)个数的平均数为( )
B.
C. D.
C
2.若x1,x2,…, xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,… ,10xn 的平均数为 .
a+3
10a
3.王敏是班内的优秀学生,她的历次数学成绩是96,98,95,93分,但最近一次的成绩只有48分,原因是她感冒发烧抱病参加了考试。试问她的平均成绩是多少?这样评价王敏的数学水平合理吗?
解: 平均成绩是
(96+98+95+93+48)÷5 = 86(分)
用算术平均数评价王敏的数学水平不合理.
4.某同学这学期前四次数学测验的成绩依次为93、82、76 和88,马上要进行第五次数学测验了,她希望五次成绩的平均数能够达到或超过 85 分,那么,这次测验她至少要考多少分
解:若要5次成绩的平均数达到85分,则总分应达到:85×5=425(分)
已经考取的成绩为:93、82、76 和88
则最后一次至少达到分数为:425-93-82-76 -88=86(分)
5. 一组数由6个数字组成,分别是1, 2, 3, x, y, z.它们平均数是4.
(1)求x,y,z三个数的平均数;
(2)求4x+5,4y+6,4z+7的平均数.
(2)根据题意
化简
由上题可知 x+y+z=18
所以三数之和为
所以平均数为
6.某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周通过该红绿灯路口的小汽车数量与标准量相比的情况如下表:
(1)星期几通过该红绿灯路口的小汽车最少,有多少辆?星期几通过该红绿灯路口的小汽车最多,有多少辆?
解:从统计表格中得出星期四通过该红绿灯路口的小汽车最少,有93辆;星期日通过该红绿灯路口的小汽车最多,有113辆.
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
解:(8+5-2-7-6+10+13)÷7+100=103(辆),故平均每天有103辆小汽车通过这个红绿灯路口.
课堂总结
平均数
概念
计算
公式
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
20.1.1 平均数的意义
华师大版 八年级 下册
教学目标
教学目标:1. 掌握平均数的概念,会求一组数据的平均数.
2.能用平均数解决实际生活中的问题.
教学重点:算术平均数的意义和计算方法.
教学难点:体会平均数在不同情境中的应用.
新知导入
情境引入
当你听到“小亮的学习成绩比王明的成绩更好”,“A篮球队队员比B队更年轻”等诸如此类的说法时,你思考过这些话的含义吗?你知道人们是如何作出这些判断的吗?
新知讲解
合作学习
八5班第二组男生期中考试成绩 姓名 语文 数学 英语 物理 道法 历史
黎建东 103 63 86 59 88 85
苏其良 105 95 94 76 84 91
吕振贤 102 111 77 77 89 91
廖宇涵 101 109 110 81 87 89
张盛 101 112 99 71 89 87
朱多良 105 116 109 79 89 89
谢鹏洋 104 111 114 93 83 85
骆鸿建 99 117 107 78 88 89
八5班第二组女生期中考试成绩 姓名 语文 数学 英语 物理 道法 历史
符慧 109 99 91 86 88 84
羊金艳 97 118 106 87 83 95
谢忠彩 99 113 104 79 79 87
孙秀梅 105 112 94 64 86 88
男生成绩好,还是女生成绩好呢?为什么?
用什么数据作为男生或者女生成绩的代表,以便比较这一组学生中男女生成绩的优劣。
算一算:下表给出了某户居民 2010 年全年的水费缴纳情况(每两个月计费一次),请你帮这户居民算一算:平均每月缴纳多少水费?
某户居民 2010 年缴纳水费统计表
月份 2 4 6 8 10 12
水费(元) 50. 60 34. 60 41. 40 46. 00 39. 20 27. 60
平均每月水费=
移多补少
想一想:如图ABCD四个杯子中装了不同数量的小球,如果想使每个杯子的小球数量相同,你有几种方法?
7
6
5
4
3
2
1
A B C D
平均数
先和后分
平均水平
7
6
5
4
3
2
1
A B C D
求小球总数量
4个杯子平均分配
每个个杯子小球数量
7+4+3+6=20(个)
20÷4=5(个)
5(个)
这节课,我们要学习一些与平均数有关的问题.我们在小学已经学过了算术平均数,它就经常被用来作为一组数据的代表.
提炼概念
2.一般地,如果有 n 个数据 x1,x2,…,xn,我们把 表示这组数据的平均数,用“ ” 表示 ,即
1.日常生活中,我们常用平均数表示一组数据的“平均水平”.
典例精讲
例1 植树节到了,某单位组织职工开展植树竞赛,如图2反映的是植树量与人数之间的关系.
图1
图2
请根据图中信息计算:
(1) 总共有多少人参加了本次活动
(2) 总共植树多少棵
(3) 平均每人植树多少棵
解:参加本次活动的总人数是 1 + 8 + 1 +10 +8 + 3 + 1 = 32(人)
总共植树 3 × 8 + 4 × 1 + 5 × 10 + 6 × 8 + 7 ×3 + 8 × 1 =155(棵)
平均每人植树=
思考
你发现了植树总量、植树量的平均数和人数这三者之间的数量关系吗 你能解释“平均每人植树 4. 8 棵”的含义吗
植树总量=植树量的平均数×人数
平均每人植树 4. 8 棵意味着,有的人植树多于4.8棵,有的人植树少于4.8棵,多的人把多出4.8棵的部分给了少的人,最后每个人植树相同的棵数就是4.8棵.
例2 丁丁所在的八年级(1) 班共有学生 40 人.如图 是该校八年级各班学生人数分布情况
(1) 班
(2) 班
(3) 班
(4) 班
(5) 班
某校八年级各班学生人数分布图
利用扇形的大小来表示部分占总体的百分比大小的统计图叫做扇形统计图.
(1) 请计算该校八年级每班平均学生人数;
(2) 请计算各班学生人数,并绘制条形统计图
八年级(2) 班: 200 × 23% = 46(人);
八年级(3) 班: 200 × 20% = 40(人);
八年级(4) 班: 200 × 18% = 36(人);
八年级(5) 班: 200 × 19% = 38(人)
解:该校八年级学生总数为 40 ÷ 20% =200(人)
每班平均学生人数为 200 ÷ 5 = 40(人)
0
5
10
15
20
25
30
35
40
45
50
班级 初二1 初二2 初二3 初二4 初二5
人数 40 46 40 36 38
根据表格数据制作各班人数的条形统计图.
人
数
40
班级
1班
2班
3班
4班
5班
46
40
36
38
超出平均线的数量和
与
低于平均线的数量和
相 等
分析:先画坐标系,再画各个班级的条形图。
思考:左图中水平红色虚线代表平均人数40的水平线。想一想,水平线上方超出部分之和与下方不足部分之和在数量上有什么关系?
归纳概念
(1)一组数据的平均数是唯一的,它不一定是数据中的某个数据;
(2)平均数是反映数据集中趋势的一个统计量,是反映数据的平均水平(或中等水平)的一个特征量;
(3)一般情况下,平均数能体现一组数据的整体性质.
课堂练习
1.有m个数的平均数是x,n个数的平均数是y,则这(m+n)个数的平均数为( )
B.
C. D.
C
2.若x1,x2,…, xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,… ,10xn 的平均数为 .
a+3
10a
3.王敏是班内的优秀学生,她的历次数学成绩是96,98,95,93分,但最近一次的成绩只有48分,原因是她感冒发烧抱病参加了考试。试问她的平均成绩是多少?这样评价王敏的数学水平合理吗?
解: 平均成绩是
(96+98+95+93+48)÷5 = 86(分)
用算术平均数评价王敏的数学水平不合理.
4.某同学这学期前四次数学测验的成绩依次为93、82、76 和88,马上要进行第五次数学测验了,她希望五次成绩的平均数能够达到或超过 85 分,那么,这次测验她至少要考多少分
解:若要5次成绩的平均数达到85分,则总分应达到:85×5=425(分)
已经考取的成绩为:93、82、76 和88
则最后一次至少达到分数为:425-93-82-76 -88=86(分)
5. 一组数由6个数字组成,分别是1, 2, 3, x, y, z.它们平均数是4.
(1)求x,y,z三个数的平均数;
(2)求4x+5,4y+6,4z+7的平均数.
(2)根据题意
化简
由上题可知 x+y+z=18
所以三数之和为
所以平均数为
6.某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周通过该红绿灯路口的小汽车数量与标准量相比的情况如下表:
(1)星期几通过该红绿灯路口的小汽车最少,有多少辆?星期几通过该红绿灯路口的小汽车最多,有多少辆?
解:从统计表格中得出星期四通过该红绿灯路口的小汽车最少,有93辆;星期日通过该红绿灯路口的小汽车最多,有113辆.
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
解:(8+5-2-7-6+10+13)÷7+100=103(辆),故平均每天有103辆小汽车通过这个红绿灯路口.
课堂总结
平均数
概念
计算
公式
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
