5.3.2 函数的最大(小)值 课件(共53张PPT)
文档属性
| 名称 | 5.3.2 函数的最大(小)值 课件(共53张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 04:40:11 | ||
图片预览







文档简介
(共53张PPT)
5.3.2函数的最大(小)值
知识回顾
知识回顾
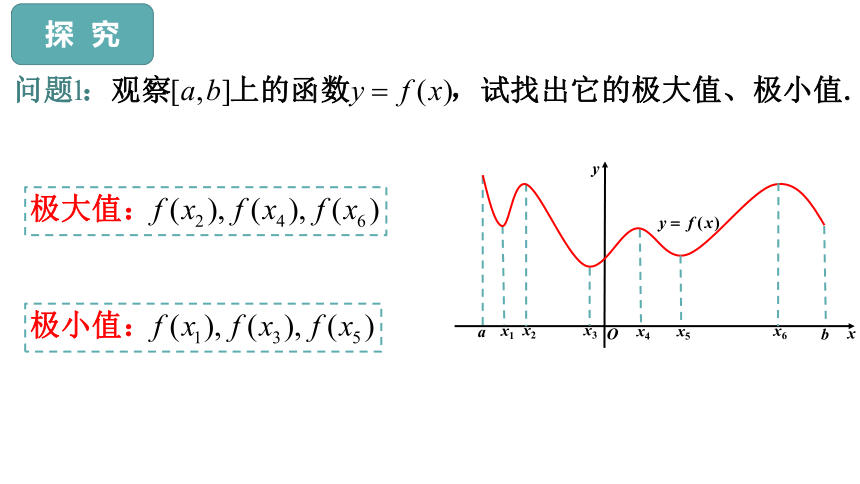
极值反映的是函数在某一点附近的局部性质
费马(1601—1665)是17世纪的法国业余数学家.之所以称费马为“业余数学家之王”,是由于他具有律师的全职工作.17世纪是杰出数学家活跃的世纪,而费马比他同时代的大多数专业数学家更有成就,是17世纪最多产的数学家之一.他将无穷小的思想运用到求积问题上,已具今日微积分的雏形,这也是费马的卓越成就之一.他在牛顿出生前就提出了有关微积分的主体概念.大约在1637年,他写了一篇手稿《求最大值与最小值的方法》.让我们沿着这位传奇人物的足迹来用导数研究函数的最大(小)值问题吧!
情境
探 究
x
y
O
a
b
x1
x2
x3
x4
x5
x6
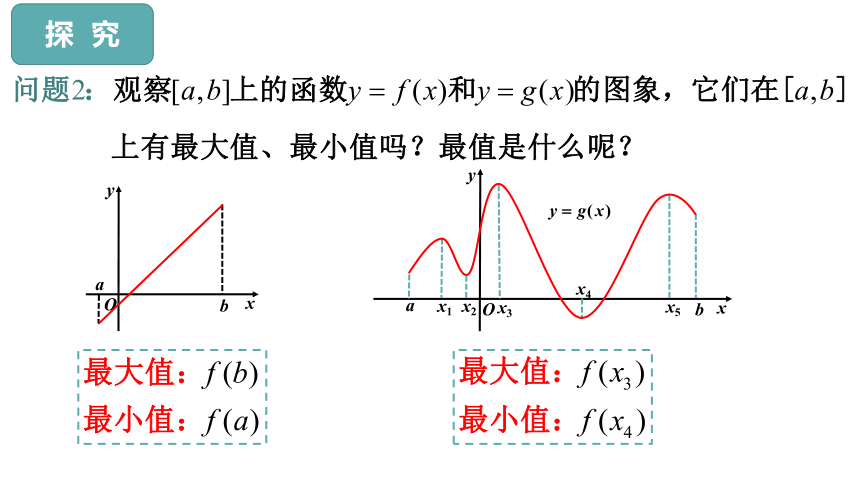
探 究
x
y
O
a
b
x1
x2
x3
x4
x5
x6
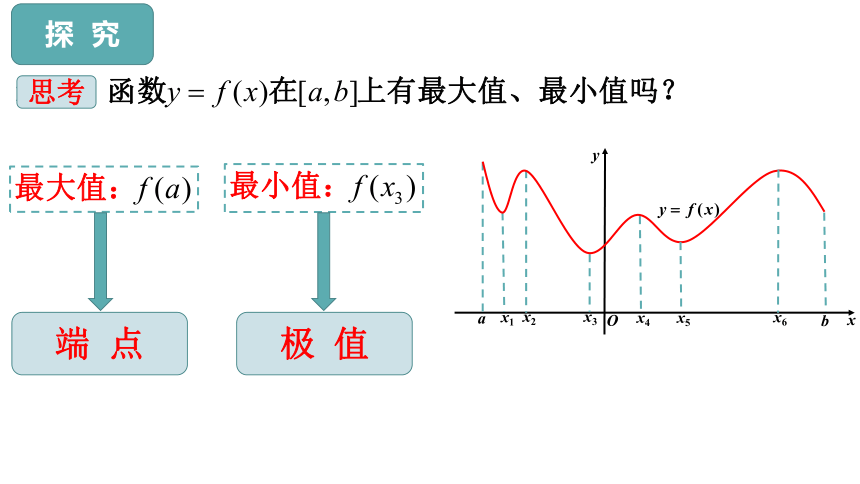
端 点
极 值
思考
探 究
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
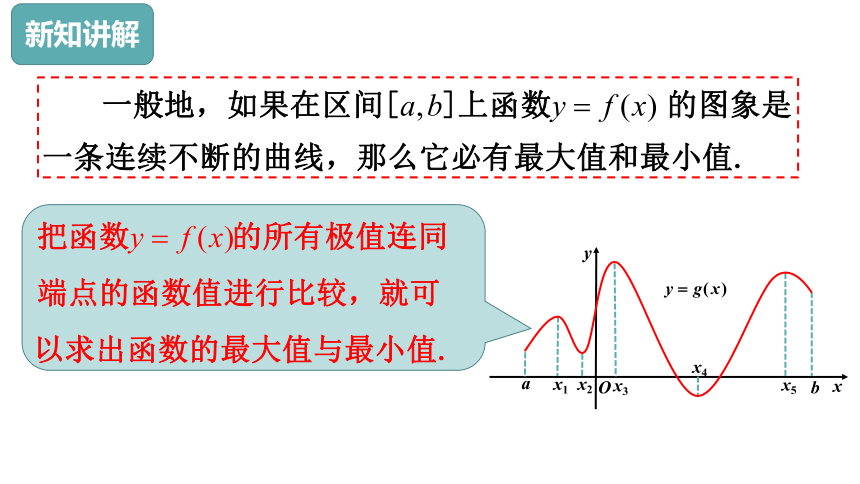
新知讲解
x
y
O
a
b
x1
x2
x3
x4
x5
深入研究
那么把闭区间换成开区间是否一定有最值呢?
那么把闭区间换成开区间是否一定有极值呢?
没有极值、有一个极值、有多个极值
没有最值、有一个最值、 情况不定
注意 给定的区间必须是闭区间,如果是开区间,尽管函数图象是连续的,那么它也不一定有最大值和最小值.例如函数f(x)=在区间(0,2)上的图象是连续不断的曲线,但在该区间上,函数f(x)既没有最大值,也没有最小值.
2.所给函数的图象必须是连续曲线,否则不一定有最大值和最小值例如函数 在[-1,1]上只有最大值,没有最小值.
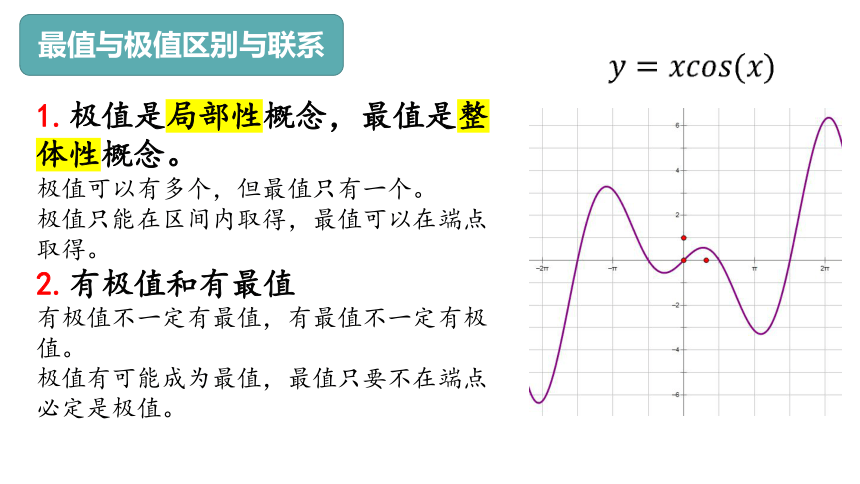
最值与极值区别与联系
1.极值是局部性概念,最值是整体性概念。
极值可以有多个,但最值只有一个。
极值只能在区间内取得,最值可以在端点取得。
2.有极值和有最值
有极值不一定有最值,有最值不一定有极值。
极值有可能成为最值,最值只要不在端点必定是极值。
微练习
设在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,且在区间(a,b)内可导,有以下三个命题:
①若f(x)在[a,b]上有最大值,则这个最大值必是[a,b]上的极大值;
②若f(x)在[a,b]上有最小值,则这个最小值必是[a,b]上的极小值;
③若f(x)在[a,b]上有最大(小)值,则最大(小)值必在x=a或 x=b处取得.
其中真命题共有( )
A.0个 B.1个 C.2个 D.3个
答案 A
解析 由于函数的最大(小)值可能在区间[a,b]的端点处取得,也可能在区间[a,b]内取得,而当最大(小)值在区间端点处取得时,其最大(小)值必不是极值,因此命题①②③都不是真命题.
探究一
求函数的最大(小)值
角度1 求函数在闭区间上的最大(小)值
例1求下列函数在相应区间上的最大值与最小值:
(2)f(x)=x3-3x2-10,x∈[-1,1];
解 (2)f'(x)=3x2-6x=3x(x-2),令f'(x)=0,得x=0(x=2舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x -1 (-1,0) 0 (0,1) 1
f'(x) + 0 -
f(x) -14 单调递增 极大值-10 单调递减 -12
所以当x=-1时,函数取最小值f(-1)=-14,当x=0时,函数取最大值f(0)=-10.
总结归纳
变式训练 1
函数f(x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是( )
A.5,15 B.5,-4
C.5,-15 D.5,-16
答案 C
解析 由已知可得函数f(x)的导数为f'(x)=6x2-6x-12,由f'(x)=6(x-2)(x+1)=0得x=2或x=-1(舍去).
当00,f(x)单调递增,所以f(x)最小值=f(x)极小值=f(2)=-15,又f(0)=5,f(3)=-4,所以f(x)最大值=5.故选C.
角度2 求函数在开区间或无穷区间上的最大(小)值
例2求下列函数的最大值与最小值:
分析没有给定相应的闭区间,因此应分析函数在其定义域上的单调性与极值情况,根据单调性与极值画出函数的大致图象,结合图象求出最大值与最小值.
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3内单调递减,因此函数f(x)在x=-3处取得极大值,极大值f(-3)=6e-3;
在x=1处取得极小值,极小值f(1)=-2e.
又由f(x)>0,得x> 或x<- ;由f(x)<0得,-方法技巧求函数在开区间或无穷区间上最大(小)值的方法
求函数在无穷区间或开区间上的最大(小)值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最大(小)值.
答案 A
探究二
含参数的最大(小)值问题
角度1 求含参数函数的最大(小)值
例3若a为常数,求函数f(x)=-x3+3ax(0≤x≤1)的最大值.
解 f'(x)=-3x2+3a=-3(x2-a).
若a≤0,则f'(x)≤0,函数f(x)单调递减,
所以当x=0时,有最大值f(0)=0.
若a>0,则令f'(x)=0,解得x=± .
∵x∈[0,1],则只考虑x= 的情况.
方法点拨求解函数在区间上的最大(小)值,需注意以下几点:
(1)对函数进行准确求导,并检验f'(x)=0的根是否在给定区间内.
(2)根据极值点与所给区间的相对位置关系(即极值点是否在区间内)确定分类讨论的标准后确定函数的极值.
(3)分类讨论后比较极值与端点函数值的大小,确定最大(小)值.
变式训练 3已知a是实数,函数f(x)=x2(x-a),求f(x)在区间[0,2]上的最大值.
角度2 与函数最大(小)值和参数有关的综合问题
例4设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
分析(1)利用配方法,即可求出二次函数f(x)的最小值h(t);(2)构造函数g(t)=h(t)-(-2t+m),只需使g(t)在(0,2)上的最大值小于零即可求得m的取值范围.
解 (1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,
即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在(0,2)内有极大值也是最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于
1-m<0.∴m的取值范围为(1,+∞).
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
反思感悟 分离参数求解不等式恒成立问题的步骤
延伸探究 1若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,则实数m的取值范围如何求解
解 令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在[0,2]上有最小值g(2)=-3-m,
存在t∈[0,2],使h(t)<-2t+m成立,
等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,故实数m的取值范围为(-3,+∞).
t 0 (0,1) 1 (1,2) 2
g'(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
延伸探究 2若将本例(2)的条件改为“对任意的t1,t2∈[0,2],都有h(t1)<-2t2+m”,求实数m的取值范围.
探究三
生活中的优化问题
例5某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
分析(1)根据x=5时,y=11求a的值;(2)把每日的利润表示为销售价格x的函数,用导数求最大值.
x (3,4) 4 (4,6)
f'(x) + 0 -
f(x) 单调递增 极大值42 单调递减
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点,所以,当x=4时,函数f(x)取得最大值,且最大值等于42.故当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
反思感悟 利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系y=f(x);
(2)求函数的导数f'(x),解方程f'(x)=0;
(3)比较函数在区间端点和极值点处的函数值的大小,最大(小)者为最大(小)值.
求解时应注意:(1)合理选择变量,正确写出函数解析式,给出函数定义域;(2)与实际问题相联系;(3)必要时注意分类讨论思想的应用.
变式训练 4请你设计一个包装盒,如图所示,四边形ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设AE=FB=x cm.
(1)某广告商要求包装盒的侧面积S(单位:cm2)最大,试问x应取何值
(2)某厂商要求包装盒的容积V(单位:cm3)最大,试问x应取何值 并求出此时包装盒的高与底面边长的比值.
素养形成
构造函数证明函数不等式
当-10,即f(x)在(-1,0)上单调递增;
当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减.
于是函数f(x)在(-1,+∞)上的最大值为f(x)max=f(0)=0,
因此,当x>-1时,f(x)≤f(0)=0,即ln(x+1)-x≤0,即ln(x+1)≤x(右边不等式得证).
当x∈(-1,0)时,g'(x)<0;当x∈(0,+∞)时,g'(x)>0.
即g(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,故函数g(x)在(-1,+∞)上的最小值为g(x)min=g(0)=0,
∴当x>-1时,g(x)≥g(0)=0,
方法点睛在函数不等式的证明中,若不等式的两边含有自变量时,可移项后构造函数,证明所构造的函数的最大(小)值与0的大小关系,常见的方法是:欲证明f(x)>g(x),可以构造函数F(x)=f(x)-g(x),只需要证明函数F(x)的最小值大于0.形如g(x)例 题
例 题
例 题
例 题
例 题
例 题
例 题
x
y
O
1
-1
-2
例 题
总结归纳
谢谢观看!
5.3.2函数的最大(小)值
知识回顾
知识回顾
极值反映的是函数在某一点附近的局部性质
费马(1601—1665)是17世纪的法国业余数学家.之所以称费马为“业余数学家之王”,是由于他具有律师的全职工作.17世纪是杰出数学家活跃的世纪,而费马比他同时代的大多数专业数学家更有成就,是17世纪最多产的数学家之一.他将无穷小的思想运用到求积问题上,已具今日微积分的雏形,这也是费马的卓越成就之一.他在牛顿出生前就提出了有关微积分的主体概念.大约在1637年,他写了一篇手稿《求最大值与最小值的方法》.让我们沿着这位传奇人物的足迹来用导数研究函数的最大(小)值问题吧!
情境
探 究
x
y
O
a
b
x1
x2
x3
x4
x5
x6
探 究
x
y
O
a
b
x1
x2
x3
x4
x5
x6
端 点
极 值
思考
探 究
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
新知讲解
x
y
O
a
b
x1
x2
x3
x4
x5
深入研究
那么把闭区间换成开区间是否一定有最值呢?
那么把闭区间换成开区间是否一定有极值呢?
没有极值、有一个极值、有多个极值
没有最值、有一个最值、 情况不定
注意 给定的区间必须是闭区间,如果是开区间,尽管函数图象是连续的,那么它也不一定有最大值和最小值.例如函数f(x)=在区间(0,2)上的图象是连续不断的曲线,但在该区间上,函数f(x)既没有最大值,也没有最小值.
2.所给函数的图象必须是连续曲线,否则不一定有最大值和最小值例如函数 在[-1,1]上只有最大值,没有最小值.
最值与极值区别与联系
1.极值是局部性概念,最值是整体性概念。
极值可以有多个,但最值只有一个。
极值只能在区间内取得,最值可以在端点取得。
2.有极值和有最值
有极值不一定有最值,有最值不一定有极值。
极值有可能成为最值,最值只要不在端点必定是极值。
微练习
设在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,且在区间(a,b)内可导,有以下三个命题:
①若f(x)在[a,b]上有最大值,则这个最大值必是[a,b]上的极大值;
②若f(x)在[a,b]上有最小值,则这个最小值必是[a,b]上的极小值;
③若f(x)在[a,b]上有最大(小)值,则最大(小)值必在x=a或 x=b处取得.
其中真命题共有( )
A.0个 B.1个 C.2个 D.3个
答案 A
解析 由于函数的最大(小)值可能在区间[a,b]的端点处取得,也可能在区间[a,b]内取得,而当最大(小)值在区间端点处取得时,其最大(小)值必不是极值,因此命题①②③都不是真命题.
探究一
求函数的最大(小)值
角度1 求函数在闭区间上的最大(小)值
例1求下列函数在相应区间上的最大值与最小值:
(2)f(x)=x3-3x2-10,x∈[-1,1];
解 (2)f'(x)=3x2-6x=3x(x-2),令f'(x)=0,得x=0(x=2舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x -1 (-1,0) 0 (0,1) 1
f'(x) + 0 -
f(x) -14 单调递增 极大值-10 单调递减 -12
所以当x=-1时,函数取最小值f(-1)=-14,当x=0时,函数取最大值f(0)=-10.
总结归纳
变式训练 1
函数f(x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是( )
A.5,15 B.5,-4
C.5,-15 D.5,-16
答案 C
解析 由已知可得函数f(x)的导数为f'(x)=6x2-6x-12,由f'(x)=6(x-2)(x+1)=0得x=2或x=-1(舍去).
当0
角度2 求函数在开区间或无穷区间上的最大(小)值
例2求下列函数的最大值与最小值:
分析没有给定相应的闭区间,因此应分析函数在其定义域上的单调性与极值情况,根据单调性与极值画出函数的大致图象,结合图象求出最大值与最小值.
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3
在x=1处取得极小值,极小值f(1)=-2e.
又由f(x)>0,得x> 或x<- ;由f(x)<0得,-
求函数在无穷区间或开区间上的最大(小)值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最大(小)值.
答案 A
探究二
含参数的最大(小)值问题
角度1 求含参数函数的最大(小)值
例3若a为常数,求函数f(x)=-x3+3ax(0≤x≤1)的最大值.
解 f'(x)=-3x2+3a=-3(x2-a).
若a≤0,则f'(x)≤0,函数f(x)单调递减,
所以当x=0时,有最大值f(0)=0.
若a>0,则令f'(x)=0,解得x=± .
∵x∈[0,1],则只考虑x= 的情况.
方法点拨求解函数在区间上的最大(小)值,需注意以下几点:
(1)对函数进行准确求导,并检验f'(x)=0的根是否在给定区间内.
(2)根据极值点与所给区间的相对位置关系(即极值点是否在区间内)确定分类讨论的标准后确定函数的极值.
(3)分类讨论后比较极值与端点函数值的大小,确定最大(小)值.
变式训练 3已知a是实数,函数f(x)=x2(x-a),求f(x)在区间[0,2]上的最大值.
角度2 与函数最大(小)值和参数有关的综合问题
例4设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
分析(1)利用配方法,即可求出二次函数f(x)的最小值h(t);(2)构造函数g(t)=h(t)-(-2t+m),只需使g(t)在(0,2)上的最大值小于零即可求得m的取值范围.
解 (1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,
即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在(0,2)内有极大值也是最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于
1-m<0.∴m的取值范围为(1,+∞).
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
反思感悟 分离参数求解不等式恒成立问题的步骤
延伸探究 1若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,则实数m的取值范围如何求解
解 令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在[0,2]上有最小值g(2)=-3-m,
存在t∈[0,2],使h(t)<-2t+m成立,
等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,故实数m的取值范围为(-3,+∞).
t 0 (0,1) 1 (1,2) 2
g'(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
延伸探究 2若将本例(2)的条件改为“对任意的t1,t2∈[0,2],都有h(t1)<-2t2+m”,求实数m的取值范围.
探究三
生活中的优化问题
例5某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
分析(1)根据x=5时,y=11求a的值;(2)把每日的利润表示为销售价格x的函数,用导数求最大值.
x (3,4) 4 (4,6)
f'(x) + 0 -
f(x) 单调递增 极大值42 单调递减
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点,所以,当x=4时,函数f(x)取得最大值,且最大值等于42.故当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
反思感悟 利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系y=f(x);
(2)求函数的导数f'(x),解方程f'(x)=0;
(3)比较函数在区间端点和极值点处的函数值的大小,最大(小)者为最大(小)值.
求解时应注意:(1)合理选择变量,正确写出函数解析式,给出函数定义域;(2)与实际问题相联系;(3)必要时注意分类讨论思想的应用.
变式训练 4请你设计一个包装盒,如图所示,四边形ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设AE=FB=x cm.
(1)某广告商要求包装盒的侧面积S(单位:cm2)最大,试问x应取何值
(2)某厂商要求包装盒的容积V(单位:cm3)最大,试问x应取何值 并求出此时包装盒的高与底面边长的比值.
素养形成
构造函数证明函数不等式
当-1
当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减.
于是函数f(x)在(-1,+∞)上的最大值为f(x)max=f(0)=0,
因此,当x>-1时,f(x)≤f(0)=0,即ln(x+1)-x≤0,即ln(x+1)≤x(右边不等式得证).
当x∈(-1,0)时,g'(x)<0;当x∈(0,+∞)时,g'(x)>0.
即g(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,故函数g(x)在(-1,+∞)上的最小值为g(x)min=g(0)=0,
∴当x>-1时,g(x)≥g(0)=0,
方法点睛在函数不等式的证明中,若不等式的两边含有自变量时,可移项后构造函数,证明所构造的函数的最大(小)值与0的大小关系,常见的方法是:欲证明f(x)>g(x),可以构造函数F(x)=f(x)-g(x),只需要证明函数F(x)的最小值大于0.形如g(x)
例 题
例 题
例 题
例 题
例 题
例 题
x
y
O
1
-1
-2
例 题
总结归纳
谢谢观看!
