5.3.2函数的极值 课件(共51张PPT)
文档属性
| 名称 | 5.3.2函数的极值 课件(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 04:41:08 | ||
图片预览







文档简介
(共51张PPT)
5.3.2函数的极值
课标阐释
思维脉络
1.了解函数的极值、极值点的概念.(数学抽象)
2.理解函数在某点取得极值的条件.(逻辑推理)
3.会利用导数求函数的极值.(数学运算)
知识回顾
问题1:如何判断函数的单调性?
定义法;
函数图象法;
导函数的正负.
知识回顾
增
减
知识回顾
定义域
零点
零点
正负
思考
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减。如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
情境
苏轼在《题西林壁》中这样写道:“横看成岭侧成峰,远近高低各不同”,描述的就是庐山的高低起伏,错落有致。各个山峰的顶端,虽然不是群山的最高处,但它却是其附近的最高点。
那么,在数学上,这种现象如何来刻画呢?
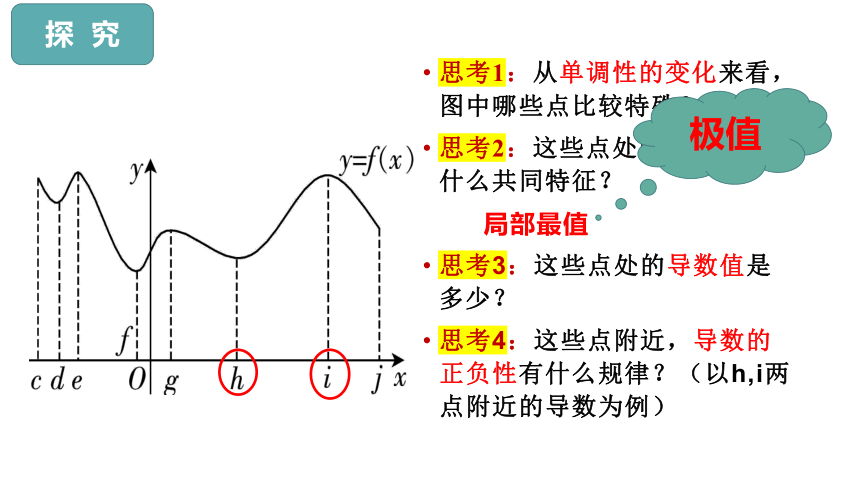
探 究
思考1:从单调性的变化来看,图中哪些点比较特殊?
思考2:这些点处的函数值有什么共同特征?
局部最值
思考3:这些点处的导数值是多少?
思考4:这些点附近,导数的正负性有什么规律?(以h,i两点附近的导数为例)
极值
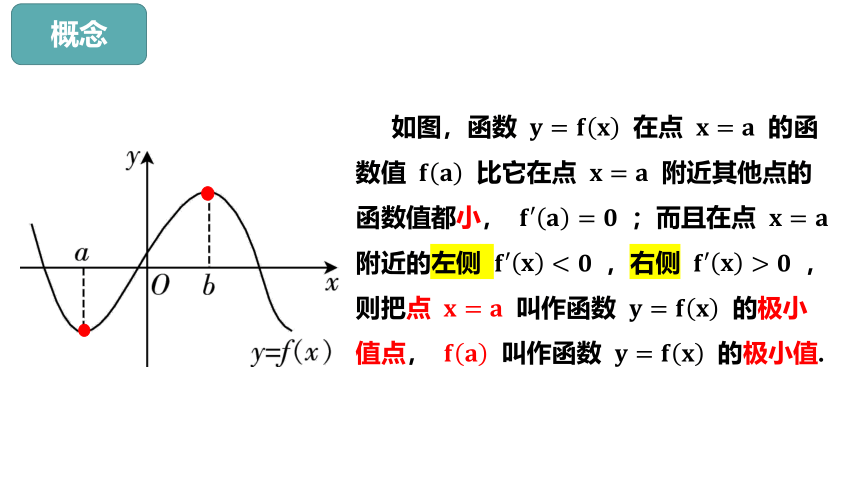
概念
如图,函数 在点 的函数值 比它在点 附近其他点的函数值都小, ;而且在点 附近的左侧 ,右侧 ,则把点 叫作函数 的极小值点, 叫作函数 的极小值.
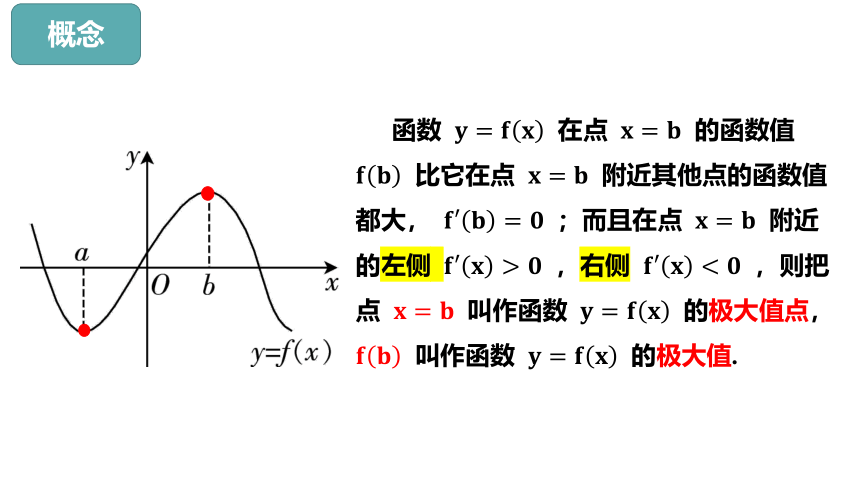
概念
函数 在点 的函数值 比它在点 附近其他点的函数值都大, ;而且在点 附近的左侧 ,右侧 ,则把点 叫作函数 的极大值点, 叫作函数 的极大值.
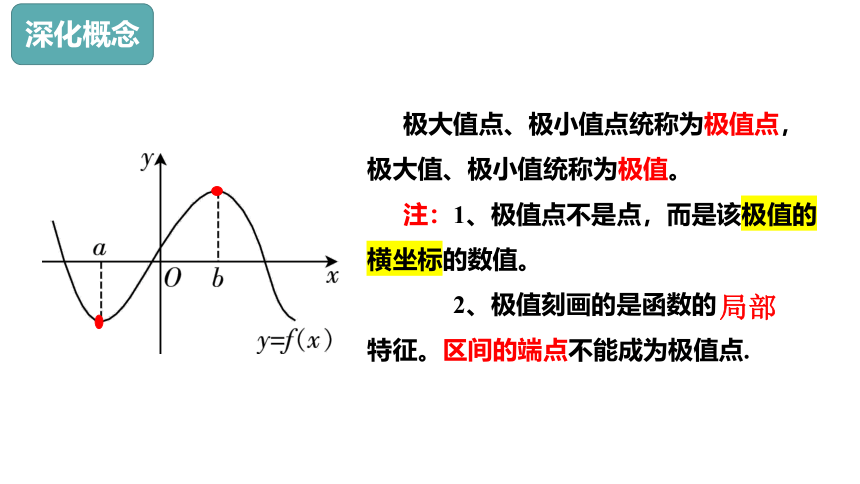
深化概念
极大值点、极小值点统称为极值点, 极大值、极小值统称为极值。
注:1、极值点不是点,而是该极值的横坐标的数值。
2、极值刻画的是函数的 特征。区间的端点不能成为极值点.
局部
x
y
O
a
b
c
d
e
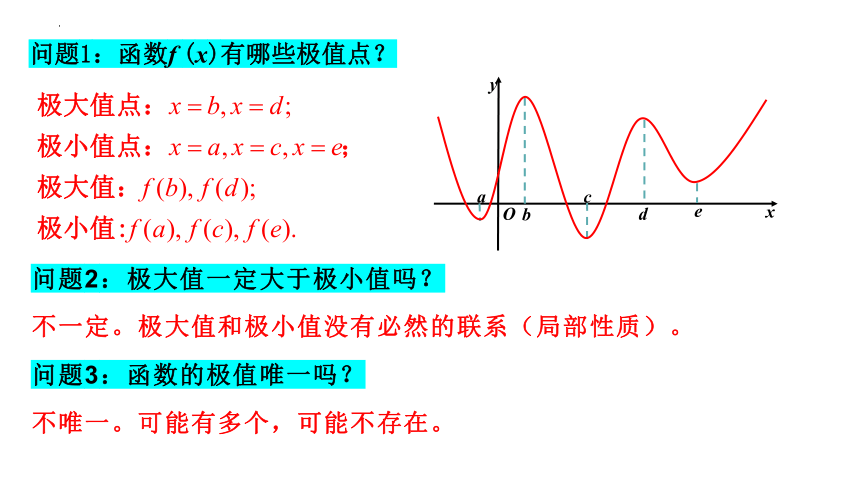
问题1:函数f (x)有哪些极值点?
问题2:极大值一定大于极小值吗?
不一定。极大值和极小值没有必然的联系(局部性质)。
问题3:函数的极值唯一吗?
不唯一。可能有多个,可能不存在。
微练习
判断下列函数是否有极值,如果有,说出是极大值还是极小值。
1、=2
2、=x
3、=-x2+3x-5
4、=sinx
无极值
无极值
有极大值,无极小值
有极大值和极小值
某区间上的单调函数没有极值
a
b
x
y
x1
O
x2
x3
x4
x5
x6
探究一
由函数图象分析函数的极值
a
b
x
y
x1
O
x2
x3
x4
x5
x6
a
b
x
y
x1
O
x2
x3
x4
x5
x6
a
b
x
y
x1
O
x2
x3
x4
x5
x6
问题4 导数值为0的点一定是函数的极值点吗?
那么,极值存在的条件是什么?
若函数有极值点,则在极值点处导数为0,但导数为0的点可能不是函数的极值点.也就是说,“f'(c)=0”是“f (x)在x=c处取到极值”的必要条件.
探究三
由函数图象分析函数的极值
例1 已知函数y=xf'(x)的图象如图所示(其中f'(x) 是函数f(x)的导函数),给出以下说法:①函数f(x)在区间(1,+∞)内单调递增;②函数f(x)在x=-1处取得极大值;③函数f(x)在x=- 处取得极大值;④函数f(x)在x=1处取得极小值,其中正确的说法有 .(填序号)
分析通过图象考查f'(x)在相关区间上的符号,以及在相关各点的左右两侧的导数值是否异号,结合极值的定义进行判断.
答案 ①②④
解析 从图象上可以发现,当x∈(1,+∞)时,xf'(x)>0,于是f'(x)>0,故f(x)在区间(1,+∞)内单调递增,①正确;当x∈(-∞,-1)时,xf'(x)<0,所以f'(x)>0,当x∈(-1,0)时,xf'(x)>0,所以f'(x)<0,故函数f(x)在x=-1处取得极大值,②正确;当x∈(0,1)时,xf'(x)<0,于是f'(x)<0,故f(x)在区间(0,1)内单调递减,而在区间(1,+∞)上单调递增,所以函数f(x)在x=1处取得极小值,④正确;当x∈(-1,1)时,f'(x)<0,所以函数f(x)在区间(-1,1)内单调递减,③错误.
方法技巧根据导函数的图象确定函数的极值的方法
根据导函数的图象确定函数的极值的方法主要是根据导函数的符号确定函数的单调性及单调区间,然后结合函数单调性确定函数的极值.
变式训练1 如图是函数y=f(x)的导函数y=f'(x)的图象,下列说法错误的是( )
A.-2是函数y=f(x)的极小值点
B.1是函数y=f(x)的极值点
C.y=f(x)在x=0处的切线的斜率大于零
D.y=f(x)在区间(-2,2)内单调递增
答案 B
解析 f'(1)=0,但在x=1附近的左、右两侧的导函数值同号,则1不是f(x)的极值点,故选B.
变式训练1 已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:
①函数f(x)在(-2,-1)和(1,2)内单调递增;
②函数f(x)在(-2,0)内单调递增,在(0,2)内单调递减;
③函数f(x)在x=-1处取得极大值,在x=1处取得极小值;
④函数f(x)在x=0处取得极大值.
其中正确结论的序号是 .
答案 ②④
解析 因为f'(x)在(-2,0)内大于0,所以函数f(x)在(-2,0)内单调递增,同理f(x)在(0,2)内单调递减,故函数f(x)在x=0处取得极大值,故②④正确.
探究二
求函数的极值
角度1 不含参数的函数求极值
例2 求下列函数的极值:
分析求出函数的导数,在函数定义域限制之下研究函数的单调性后,确定极值.
解 (1)函数的定义域为R,f'(x)=x2-2x-3.
令f'(x)=0,得x=3或x=-1.
当x变化时,f'(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f'(x) + 0 - 0 +
f(x) 单调递增 极大值 单调递减 极小值-6 单调递增
∴x=-1是f(x)的极大值点,x=3是f(x)的极小值点.
∴f(x)极大值= ,f(x)极小值=-6.
归纳总结
(2)已知函数f (x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,则实数a的取值范围是________.
解 (1)函数f(x)的定义域为R,
f'(x)= =x(2-x)e-x.
令f'(x)=0,得x(2-x)·e-x=0,
解得x=0或x=2.
当x变化时,f'(x),f(x)的变化情况如下表:
因此,当x=0时,f(x)有极小值,并且极小值为f(0)=0;当x=2时,f(x)有极大值,并且极大值为f(2)= .
x (-∞,0) 0 (0,2) 2 (2,+∞)
f'(x) - 0 + 0 -
f(x) 单调递减 极小值0 单调递增 极大值4e-2 单调递减
(2) (-∞,-1)∪(2,+∞) [f ′(x)=3x2+6ax+3(a+2),∵函数f (x)既有极大值又有极小值,∴方程f ′(x)=0有两个不相等的实根,∴Δ=36a2-36(a+2)>0,即a2-a-2>0,解得a>2或a<-1.]
角度2 含参数的函数求极值
例3已知函数f(x)= x3-(a+1)x2+4ax+2(a为实数),求函数f(x)的极值.
分析对函数f(x)求导,得到f'(x)=x2-2(a+1)x+4a=(x-2)(x-2a),根据导函数的零点2和2a的大小,分类讨论函数的单调性,根据函数的单调性确定函数的极值.
解 ∵f(x)=x3-(a+1)x2+4ax+2,
∴f'(x)=x2-2(a+1)x+4a=(x-2)(x-2a).
令f'(x)=0,解得x=2或x=2a.
(1)当a=1时,2a=2,因此f'(x)=(x-2)2≥0,故f(x)在R上单调递增,不存在极值;
(2)当a<1时,2a<2,当x变化时,f(x),f'(x)随x的变化情况如下表:
x (-∞,2a) 2a (2a,2) 2 (2,+∞)
g'(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
由上表可知f(x)在(-∞,2a)和(2,+∞)上单调递增,在(2a,2)上单调递减,
方法技巧解析式中含参数的函数极值的求法
1.根据参数对导函数的零点的影响确定分类讨论的标准(导函数是否存在零点以及导函数存在零点时零点的大小)
2.根据函数的单调区间确定函数的极值.
变式训练3 若函数f(x)=x-aln x(a∈R),求函数f(x)的极值.
解 函数f(x)的定义域为(0,+∞),f'(x)=
(1)当a≤0时,f'(x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)无极值.
(2)当a>0时,令f'(x)=0,解得x=a.
当0当x>a时,f'(x)>0.
则f(x)在x=a处取得极小值,且f(a)=a-aln a,无极大值.
综上可知,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
探究三
由极值求参数的值或取值范围
角度1 根据极值求参数值
例4 已知函数f(x)=x3+ax2+bx+4在x=1处取得极值 .
(1)求a,b的值;
(2)求函数的另一个极值.
分析(1)可利用f'(1)=0,f(1)= 建立关于a,b的方程组求解;(2)按照求极值的步骤求解.
变式训练4 (1)函数f(x)=ax3+bx在x=1处有极值-2,则a,b的值分别为( )
A.1,-3 B.1,3
C.-1,3 D.-1,-3
(2)(2021湖南长沙湖南师大附中高二月考)已知函数f(x)=x3+3mx2+nx+m2在x=-1处取得极值0,则m+n=( )
A.4 B.11
C.4或11 D.3或9
答案 (1)A (2)B
角度2 根据极值点个数求参数取值范围
例5 已知函数f(x)= x3- (m+3)x2+(m+6)x(x∈R,m为常数),在区间(1,+∞)内有两个极值点,求实数m的取值范围.
分析f(x)在(1,+∞)内有两个极值点,等价于f'(x)=0在(1,+∞)内有两个不等实根.
解 f'(x)=x2-(m+3)x+m+6.
因为函数f(x)在(1,+∞)内有两个极值点,
所以f'(x)=x2-(m+3)x+m+6在(1,+∞)内与x轴有两个不同的交点,如图所示.
解得m>3.故实数m的取值范围是(3,+∞).
变式训练5 (1)(2021宁夏固原隆德高二期末)函数f(x)=x3+3ax2+3[(a+2)x+1]既有极大值又有极小值,则a的取值范围是( )
A.(-1,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-∞,-1)∪(2,+∞)
解析 (1)∵f(x)=x3+3ax2+3[(a+2)x+1],
∴f'(x)=3x2+6ax+3(a+2).
∵函数f(x)有极大值又有极小值,
∴f'(x)=0有两个不相等的实数根,
∴Δ=36a2-36(a+2)>0,
整理可得a2-a-2>0,解得a>2或a<-1.
故a的取值范围是(-∞,-1)∪(2,+∞).故选D.
当00,当x>1时,f'(x)<0.
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴函数f(x)在x=1处取得极大值.
素养形成
利用函数极值研究函数零点
典例 已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
分析求出函数的极值,要使f(x)=0有三个不同实根,则应有极大值大于0,极小值小于0,由此可得a的取值范围.
解 令f'(x)=3x2-3=3(x+1)(x-1)=0,解得x1=-1,x2=1.
当x<-1时,f'(x)>0;
当-1当x>1时,f'(x)>0.
所以当x=-1时,f(x)有极大值f(-1)=2+a;
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,
所以y=f(x)的图象与x轴有三个交点,如图.
解得-2小结
2.求函数极值的方法和步骤
1.函数极值点与极值概念
1.函数f (x)的定义域为R,它的导函数y=f ′(x)的部分图象如图所示,则下面结论错误的是( )
A.在(1,2)上函数f (x)为增函数
B.在(3,4)上函数f (x)为减函数C.在(1,3)上函数f (x)有极大值D.x=3是函数f (x)在区间[1,5]上的极小值点
课堂达标
1. D [由题图可知,当1<x<2时,f ′(x)>0,当2<x<4时,f ′(x)<0,当4<x<5时,f ′(x)>0,∴x=2是函数f (x)的极大值点,x=4是函数f (x)的极小值点,故A,B,C正确,D错误.]
2.设函数f (x)=xex,则( )A.x=1为f (x)的极大值点B.x=1为f (x)的极小值点C.x=-1为f (x)的极大值点D.x=-1为f (x)的极小值点
3.已知函数f (x)=2ef ′(e)ln x-,则函数f (x)的极大值为______.
2. D [令f ′(x)=ex+x·ex=(1+x)ex=0,得x=-1.当x<-1时,f ′(x)<0;当x>-1时,f ′(x)>0.故当x=-1时,f (x)取得极小值.]
3. 2ln 2 [f ′(x)=(e)x(2ef′)-e(1),故f ′(e)=(e)e(2ef′)-e(1),解得f ′(e)=e(1),所以f (x)=2ln x-e(x),f ′(x)=x(2)-e(1).由f ′(x)>0得0<x<2e,f ′(x)<0得x>2e.所以函数f (x)在(0,2e)单调递增,在(2e,+∞)单调递减,故f (x)的极大值为f (2e)=2ln 2e-2=2ln 2.]
谢谢观看!
5.3.2函数的极值
课标阐释
思维脉络
1.了解函数的极值、极值点的概念.(数学抽象)
2.理解函数在某点取得极值的条件.(逻辑推理)
3.会利用导数求函数的极值.(数学运算)
知识回顾
问题1:如何判断函数的单调性?
定义法;
函数图象法;
导函数的正负.
知识回顾
增
减
知识回顾
定义域
零点
零点
正负
思考
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减。如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
情境
苏轼在《题西林壁》中这样写道:“横看成岭侧成峰,远近高低各不同”,描述的就是庐山的高低起伏,错落有致。各个山峰的顶端,虽然不是群山的最高处,但它却是其附近的最高点。
那么,在数学上,这种现象如何来刻画呢?
探 究
思考1:从单调性的变化来看,图中哪些点比较特殊?
思考2:这些点处的函数值有什么共同特征?
局部最值
思考3:这些点处的导数值是多少?
思考4:这些点附近,导数的正负性有什么规律?(以h,i两点附近的导数为例)
极值
概念
如图,函数 在点 的函数值 比它在点 附近其他点的函数值都小, ;而且在点 附近的左侧 ,右侧 ,则把点 叫作函数 的极小值点, 叫作函数 的极小值.
概念
函数 在点 的函数值 比它在点 附近其他点的函数值都大, ;而且在点 附近的左侧 ,右侧 ,则把点 叫作函数 的极大值点, 叫作函数 的极大值.
深化概念
极大值点、极小值点统称为极值点, 极大值、极小值统称为极值。
注:1、极值点不是点,而是该极值的横坐标的数值。
2、极值刻画的是函数的 特征。区间的端点不能成为极值点.
局部
x
y
O
a
b
c
d
e
问题1:函数f (x)有哪些极值点?
问题2:极大值一定大于极小值吗?
不一定。极大值和极小值没有必然的联系(局部性质)。
问题3:函数的极值唯一吗?
不唯一。可能有多个,可能不存在。
微练习
判断下列函数是否有极值,如果有,说出是极大值还是极小值。
1、=2
2、=x
3、=-x2+3x-5
4、=sinx
无极值
无极值
有极大值,无极小值
有极大值和极小值
某区间上的单调函数没有极值
a
b
x
y
x1
O
x2
x3
x4
x5
x6
探究一
由函数图象分析函数的极值
a
b
x
y
x1
O
x2
x3
x4
x5
x6
a
b
x
y
x1
O
x2
x3
x4
x5
x6
a
b
x
y
x1
O
x2
x3
x4
x5
x6
问题4 导数值为0的点一定是函数的极值点吗?
那么,极值存在的条件是什么?
若函数有极值点,则在极值点处导数为0,但导数为0的点可能不是函数的极值点.也就是说,“f'(c)=0”是“f (x)在x=c处取到极值”的必要条件.
探究三
由函数图象分析函数的极值
例1 已知函数y=xf'(x)的图象如图所示(其中f'(x) 是函数f(x)的导函数),给出以下说法:①函数f(x)在区间(1,+∞)内单调递增;②函数f(x)在x=-1处取得极大值;③函数f(x)在x=- 处取得极大值;④函数f(x)在x=1处取得极小值,其中正确的说法有 .(填序号)
分析通过图象考查f'(x)在相关区间上的符号,以及在相关各点的左右两侧的导数值是否异号,结合极值的定义进行判断.
答案 ①②④
解析 从图象上可以发现,当x∈(1,+∞)时,xf'(x)>0,于是f'(x)>0,故f(x)在区间(1,+∞)内单调递增,①正确;当x∈(-∞,-1)时,xf'(x)<0,所以f'(x)>0,当x∈(-1,0)时,xf'(x)>0,所以f'(x)<0,故函数f(x)在x=-1处取得极大值,②正确;当x∈(0,1)时,xf'(x)<0,于是f'(x)<0,故f(x)在区间(0,1)内单调递减,而在区间(1,+∞)上单调递增,所以函数f(x)在x=1处取得极小值,④正确;当x∈(-1,1)时,f'(x)<0,所以函数f(x)在区间(-1,1)内单调递减,③错误.
方法技巧根据导函数的图象确定函数的极值的方法
根据导函数的图象确定函数的极值的方法主要是根据导函数的符号确定函数的单调性及单调区间,然后结合函数单调性确定函数的极值.
变式训练1 如图是函数y=f(x)的导函数y=f'(x)的图象,下列说法错误的是( )
A.-2是函数y=f(x)的极小值点
B.1是函数y=f(x)的极值点
C.y=f(x)在x=0处的切线的斜率大于零
D.y=f(x)在区间(-2,2)内单调递增
答案 B
解析 f'(1)=0,但在x=1附近的左、右两侧的导函数值同号,则1不是f(x)的极值点,故选B.
变式训练1 已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:
①函数f(x)在(-2,-1)和(1,2)内单调递增;
②函数f(x)在(-2,0)内单调递增,在(0,2)内单调递减;
③函数f(x)在x=-1处取得极大值,在x=1处取得极小值;
④函数f(x)在x=0处取得极大值.
其中正确结论的序号是 .
答案 ②④
解析 因为f'(x)在(-2,0)内大于0,所以函数f(x)在(-2,0)内单调递增,同理f(x)在(0,2)内单调递减,故函数f(x)在x=0处取得极大值,故②④正确.
探究二
求函数的极值
角度1 不含参数的函数求极值
例2 求下列函数的极值:
分析求出函数的导数,在函数定义域限制之下研究函数的单调性后,确定极值.
解 (1)函数的定义域为R,f'(x)=x2-2x-3.
令f'(x)=0,得x=3或x=-1.
当x变化时,f'(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f'(x) + 0 - 0 +
f(x) 单调递增 极大值 单调递减 极小值-6 单调递增
∴x=-1是f(x)的极大值点,x=3是f(x)的极小值点.
∴f(x)极大值= ,f(x)极小值=-6.
归纳总结
(2)已知函数f (x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,则实数a的取值范围是________.
解 (1)函数f(x)的定义域为R,
f'(x)= =x(2-x)e-x.
令f'(x)=0,得x(2-x)·e-x=0,
解得x=0或x=2.
当x变化时,f'(x),f(x)的变化情况如下表:
因此,当x=0时,f(x)有极小值,并且极小值为f(0)=0;当x=2时,f(x)有极大值,并且极大值为f(2)= .
x (-∞,0) 0 (0,2) 2 (2,+∞)
f'(x) - 0 + 0 -
f(x) 单调递减 极小值0 单调递增 极大值4e-2 单调递减
(2) (-∞,-1)∪(2,+∞) [f ′(x)=3x2+6ax+3(a+2),∵函数f (x)既有极大值又有极小值,∴方程f ′(x)=0有两个不相等的实根,∴Δ=36a2-36(a+2)>0,即a2-a-2>0,解得a>2或a<-1.]
角度2 含参数的函数求极值
例3已知函数f(x)= x3-(a+1)x2+4ax+2(a为实数),求函数f(x)的极值.
分析对函数f(x)求导,得到f'(x)=x2-2(a+1)x+4a=(x-2)(x-2a),根据导函数的零点2和2a的大小,分类讨论函数的单调性,根据函数的单调性确定函数的极值.
解 ∵f(x)=x3-(a+1)x2+4ax+2,
∴f'(x)=x2-2(a+1)x+4a=(x-2)(x-2a).
令f'(x)=0,解得x=2或x=2a.
(1)当a=1时,2a=2,因此f'(x)=(x-2)2≥0,故f(x)在R上单调递增,不存在极值;
(2)当a<1时,2a<2,当x变化时,f(x),f'(x)随x的变化情况如下表:
x (-∞,2a) 2a (2a,2) 2 (2,+∞)
g'(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
由上表可知f(x)在(-∞,2a)和(2,+∞)上单调递增,在(2a,2)上单调递减,
方法技巧解析式中含参数的函数极值的求法
1.根据参数对导函数的零点的影响确定分类讨论的标准(导函数是否存在零点以及导函数存在零点时零点的大小)
2.根据函数的单调区间确定函数的极值.
变式训练3 若函数f(x)=x-aln x(a∈R),求函数f(x)的极值.
解 函数f(x)的定义域为(0,+∞),f'(x)=
(1)当a≤0时,f'(x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)无极值.
(2)当a>0时,令f'(x)=0,解得x=a.
当0
则f(x)在x=a处取得极小值,且f(a)=a-aln a,无极大值.
综上可知,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
探究三
由极值求参数的值或取值范围
角度1 根据极值求参数值
例4 已知函数f(x)=x3+ax2+bx+4在x=1处取得极值 .
(1)求a,b的值;
(2)求函数的另一个极值.
分析(1)可利用f'(1)=0,f(1)= 建立关于a,b的方程组求解;(2)按照求极值的步骤求解.
变式训练4 (1)函数f(x)=ax3+bx在x=1处有极值-2,则a,b的值分别为( )
A.1,-3 B.1,3
C.-1,3 D.-1,-3
(2)(2021湖南长沙湖南师大附中高二月考)已知函数f(x)=x3+3mx2+nx+m2在x=-1处取得极值0,则m+n=( )
A.4 B.11
C.4或11 D.3或9
答案 (1)A (2)B
角度2 根据极值点个数求参数取值范围
例5 已知函数f(x)= x3- (m+3)x2+(m+6)x(x∈R,m为常数),在区间(1,+∞)内有两个极值点,求实数m的取值范围.
分析f(x)在(1,+∞)内有两个极值点,等价于f'(x)=0在(1,+∞)内有两个不等实根.
解 f'(x)=x2-(m+3)x+m+6.
因为函数f(x)在(1,+∞)内有两个极值点,
所以f'(x)=x2-(m+3)x+m+6在(1,+∞)内与x轴有两个不同的交点,如图所示.
解得m>3.故实数m的取值范围是(3,+∞).
变式训练5 (1)(2021宁夏固原隆德高二期末)函数f(x)=x3+3ax2+3[(a+2)x+1]既有极大值又有极小值,则a的取值范围是( )
A.(-1,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-∞,-1)∪(2,+∞)
解析 (1)∵f(x)=x3+3ax2+3[(a+2)x+1],
∴f'(x)=3x2+6ax+3(a+2).
∵函数f(x)有极大值又有极小值,
∴f'(x)=0有两个不相等的实数根,
∴Δ=36a2-36(a+2)>0,
整理可得a2-a-2>0,解得a>2或a<-1.
故a的取值范围是(-∞,-1)∪(2,+∞).故选D.
当0
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴函数f(x)在x=1处取得极大值.
素养形成
利用函数极值研究函数零点
典例 已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
分析求出函数的极值,要使f(x)=0有三个不同实根,则应有极大值大于0,极小值小于0,由此可得a的取值范围.
解 令f'(x)=3x2-3=3(x+1)(x-1)=0,解得x1=-1,x2=1.
当x<-1时,f'(x)>0;
当-1
所以当x=-1时,f(x)有极大值f(-1)=2+a;
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,
所以y=f(x)的图象与x轴有三个交点,如图.
解得-2
2.求函数极值的方法和步骤
1.函数极值点与极值概念
1.函数f (x)的定义域为R,它的导函数y=f ′(x)的部分图象如图所示,则下面结论错误的是( )
A.在(1,2)上函数f (x)为增函数
B.在(3,4)上函数f (x)为减函数C.在(1,3)上函数f (x)有极大值D.x=3是函数f (x)在区间[1,5]上的极小值点
课堂达标
1. D [由题图可知,当1<x<2时,f ′(x)>0,当2<x<4时,f ′(x)<0,当4<x<5时,f ′(x)>0,∴x=2是函数f (x)的极大值点,x=4是函数f (x)的极小值点,故A,B,C正确,D错误.]
2.设函数f (x)=xex,则( )A.x=1为f (x)的极大值点B.x=1为f (x)的极小值点C.x=-1为f (x)的极大值点D.x=-1为f (x)的极小值点
3.已知函数f (x)=2ef ′(e)ln x-,则函数f (x)的极大值为______.
2. D [令f ′(x)=ex+x·ex=(1+x)ex=0,得x=-1.当x<-1时,f ′(x)<0;当x>-1时,f ′(x)>0.故当x=-1时,f (x)取得极小值.]
3. 2ln 2 [f ′(x)=(e)x(2ef′)-e(1),故f ′(e)=(e)e(2ef′)-e(1),解得f ′(e)=e(1),所以f (x)=2ln x-e(x),f ′(x)=x(2)-e(1).由f ′(x)>0得0<x<2e,f ′(x)<0得x>2e.所以函数f (x)在(0,2e)单调递增,在(2e,+∞)单调递减,故f (x)的极大值为f (2e)=2ln 2e-2=2ln 2.]
谢谢观看!
