人教版(2023春)数学四年级下册9数学广角——鸡兔同笼 课件(25张PPT)
文档属性
| 名称 | 人教版(2023春)数学四年级下册9数学广角——鸡兔同笼 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 20:31:57 | ||
图片预览







文档简介
(共25张PPT)
第9单元 数学广角——鸡兔同笼
在“十一”黄金周假期的一天,爸爸和妈妈带李明到动物园游玩。他们来到动物园的小湖边,看到一些白鹤和乌龟在湖边小憩。李明好奇地问饲养员叔叔:“叔叔,这里有多少只白鹤,有多少只乌龟呀?”饲养员叔叔没有直接回答,笑着说:“龟和鹤的头一共有8个,脚一共有26只。小朋友,你自己算一算龟、鹤各有多少只?”同学们,你能解决这个问题吗?
创设情境
你们从饲养员叔叔的话中获得了哪些数学信息?
★知道了龟和鹤一共有8个头、26只脚。
★知道了一只龟有4只脚,一只鹤有2只脚。
★现在要解决的问题是“龟和鹤各有几只”。
猜测激趣
哪个小组愿意把你们的结果和大家分享一下?
★动手操作:用8张小圆纸片代表龟和鹤的“头”,用牙签代表龟和鹤的“脚”,先给每个“头”装上2只“脚”,就有了16只“脚”,然后把剩下的10只“脚”再分别加到龟上。这样,4只“脚”的就是乌龟,2只“脚”的就是鹤了,所以鹤有3只,龟有5只。
探究新知
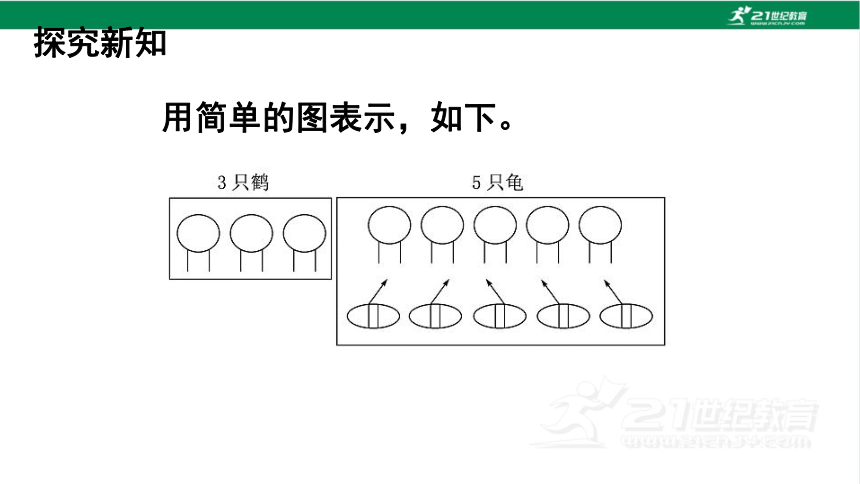
用简单的图表示,如下。
探究新知
★动手操作,但方法有些不同:先给每个“头”装上4只“脚”,有6个“头”装上了4只“脚”,剩下2只“脚”,装给剩下的2个“头”,各装上1只“脚”,要使这2个“头”都有2只“脚”,只能从有4只“脚”的一个“头”上拿下2只“脚”来装给这2个“头”,这时,5个“头”各有4只“脚”的就是乌龟,3个“头”各有2只“脚”的就是鹤,所以龟有5只,鹤有3只。
探究新知
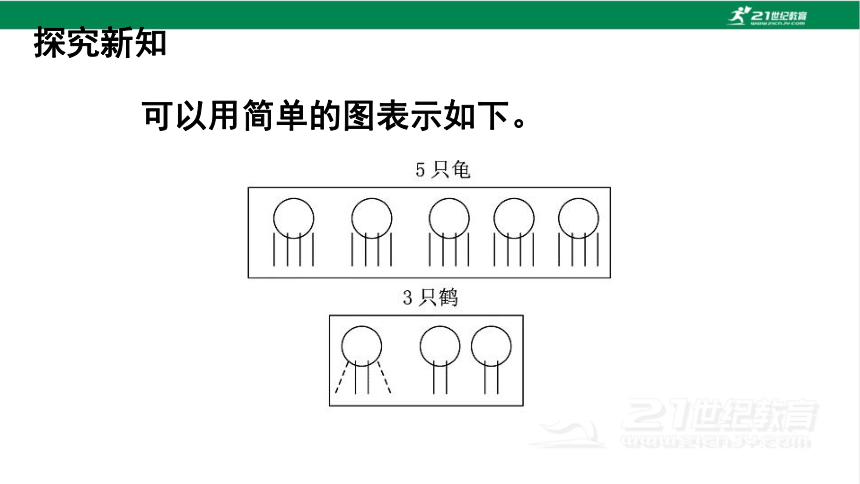
可以用简单的图表示如下。
探究新知
★一一假设,逐一验证。假如有1只龟,那么就有7只鹤,共有18只脚,与题目条件不符合;假如有2只龟,那么就有6只鹤,共有20只脚,也不符合题目条件……一直类推到:假如有5只龟,那么就有3只鹤,共有26只脚,刚好符合题目条件。
探究新知
★用表格来推算。
探究新知
鹤 8 7 6 5 4 3
龟 0 1 2 3 4 5
脚总只数 16 18 20 22 24 26
列表推算的方法也叫枚举法。
★规律:如果假设鹤的只数减少一只,龟的只数就增加一只,脚的总只数会增加2。如果假设龟有4只,鹤也有4只,这样就简便了许多。
探究新知
以上的方法属于一种猜测和推算的过程,你们有没有用列式的方法来解决这个问题的呢?
假如在这个时候远处传来一声巨响,乌龟们都好奇地站立,翘首而望,这时,它们和鹤一样只有两只脚站在地上。同学们,此情此景,你们怎样列算式解决这个问题?
探究新知
★假设龟也用2只后脚站了起来,那么在地上的脚是8×2=16只,而现在有26只脚,多出了26﹣16=10只脚。这10只脚应该是龟缩起来的,每只龟少算了2只脚,所以龟有10÷2=5只,鹤就有8﹣5=3只。
8×2=16(只) 26﹣16=10(只)
龟:10÷2=5(只) 鹤:8﹣5=3(只)
探究新知
★假设鹤不服气龟有4只脚,把两只翅膀也撑到地上当做脚,那么鹤也有4只脚,这时脚的总只数应该是8×4=32,但实际上只有26只,这是因为把鹤的翅膀当做脚来计算,鹤着地的翅膀就有32﹣26=6只,每2只翅膀就是1只鹤,所以鹤有6÷2=3只,龟就有8﹣3=5只。
探究新知
可以把刚才的这两种解决问题的方法称为假设法。
其实,我国古代数学名著《孙子算经》中就记载了这样一道有趣的数学题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”你们知道这个古代数学问题的意思吗?
激发情感
这就是著名的“鸡兔同笼”问题。现在,大家用自己喜欢的方法来解决这个问题吧。
★用假设全是鸡或全是兔的方法来解,计算起来比较快。
★用列表的方法来解答。
★先假设鸡有17只,兔有18只,这样取中间两个数的假设比较快,接近答案。
激发情感
你们想知道古人是怎样解决这个问题的吗?
激发情感
有的同学不明白为什么“47﹣35=12”就是兔子的只数,谁能解释一下?
★ “94÷2=47”表示的是总脚数的一半。这时,一只鸡一只脚,即1个头有一只脚;一只兔2只脚,即1个头2只脚。所以脚数47比头数35多的47﹣35=12就是兔子的只数。
激发情感
94÷2=47
兔:47﹣35=12(只)
鸡:35﹣12=23(只)
古人这一思路新颖而奇特,这“抬腿法”也叫“减半法”,令古今中外数学家赞叹不已。这种解法给我们的启示是:思维方式一定要灵活多变,不能墨守成规。
激发情感
38名少先队员去划船,租了8条船,每条船都坐满人,大船能坐6人,小船能坐4人。这次活动租大船、小船各几条?
谁想来汇报一下自己小组的研究结果?
延伸应用
★这是一个“鸡兔同笼”问题,大船坐的人数较多,可以看作“兔”,而小船就看作“鸡”。
★大船当“兔”,坐的6人算作“兔脚”,小船当“鸡”,坐的4人算作“鸡脚”。问题就变成有38只脚(人),8个头(船数),每只兔(大船)有6只脚(人),每只鸡(小船)有4只脚(人),鸡、兔各有几只?
延伸应用
★假设全部是大船,8条船能坐6×8=48人,比实际38人多48﹣38=10人,因为每条大船比小船多坐6﹣4=2人,所以,有10÷2=5条小船,8﹣5=3条大船。
将“租船”问题转化成“鸡兔同笼”问题。
延伸应用
今天的学习有趣吗?大家有哪些收获?
“鸡兔同笼”问题是我国三大趣题之一。希望你们能用今天学到的方法去解决更多实际生活中的数学问题。
畅谈收获
感谢聆听!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第9单元 数学广角——鸡兔同笼
在“十一”黄金周假期的一天,爸爸和妈妈带李明到动物园游玩。他们来到动物园的小湖边,看到一些白鹤和乌龟在湖边小憩。李明好奇地问饲养员叔叔:“叔叔,这里有多少只白鹤,有多少只乌龟呀?”饲养员叔叔没有直接回答,笑着说:“龟和鹤的头一共有8个,脚一共有26只。小朋友,你自己算一算龟、鹤各有多少只?”同学们,你能解决这个问题吗?
创设情境
你们从饲养员叔叔的话中获得了哪些数学信息?
★知道了龟和鹤一共有8个头、26只脚。
★知道了一只龟有4只脚,一只鹤有2只脚。
★现在要解决的问题是“龟和鹤各有几只”。
猜测激趣
哪个小组愿意把你们的结果和大家分享一下?
★动手操作:用8张小圆纸片代表龟和鹤的“头”,用牙签代表龟和鹤的“脚”,先给每个“头”装上2只“脚”,就有了16只“脚”,然后把剩下的10只“脚”再分别加到龟上。这样,4只“脚”的就是乌龟,2只“脚”的就是鹤了,所以鹤有3只,龟有5只。
探究新知
用简单的图表示,如下。
探究新知
★动手操作,但方法有些不同:先给每个“头”装上4只“脚”,有6个“头”装上了4只“脚”,剩下2只“脚”,装给剩下的2个“头”,各装上1只“脚”,要使这2个“头”都有2只“脚”,只能从有4只“脚”的一个“头”上拿下2只“脚”来装给这2个“头”,这时,5个“头”各有4只“脚”的就是乌龟,3个“头”各有2只“脚”的就是鹤,所以龟有5只,鹤有3只。
探究新知
可以用简单的图表示如下。
探究新知
★一一假设,逐一验证。假如有1只龟,那么就有7只鹤,共有18只脚,与题目条件不符合;假如有2只龟,那么就有6只鹤,共有20只脚,也不符合题目条件……一直类推到:假如有5只龟,那么就有3只鹤,共有26只脚,刚好符合题目条件。
探究新知
★用表格来推算。
探究新知
鹤 8 7 6 5 4 3
龟 0 1 2 3 4 5
脚总只数 16 18 20 22 24 26
列表推算的方法也叫枚举法。
★规律:如果假设鹤的只数减少一只,龟的只数就增加一只,脚的总只数会增加2。如果假设龟有4只,鹤也有4只,这样就简便了许多。
探究新知
以上的方法属于一种猜测和推算的过程,你们有没有用列式的方法来解决这个问题的呢?
假如在这个时候远处传来一声巨响,乌龟们都好奇地站立,翘首而望,这时,它们和鹤一样只有两只脚站在地上。同学们,此情此景,你们怎样列算式解决这个问题?
探究新知
★假设龟也用2只后脚站了起来,那么在地上的脚是8×2=16只,而现在有26只脚,多出了26﹣16=10只脚。这10只脚应该是龟缩起来的,每只龟少算了2只脚,所以龟有10÷2=5只,鹤就有8﹣5=3只。
8×2=16(只) 26﹣16=10(只)
龟:10÷2=5(只) 鹤:8﹣5=3(只)
探究新知
★假设鹤不服气龟有4只脚,把两只翅膀也撑到地上当做脚,那么鹤也有4只脚,这时脚的总只数应该是8×4=32,但实际上只有26只,这是因为把鹤的翅膀当做脚来计算,鹤着地的翅膀就有32﹣26=6只,每2只翅膀就是1只鹤,所以鹤有6÷2=3只,龟就有8﹣3=5只。
探究新知
可以把刚才的这两种解决问题的方法称为假设法。
其实,我国古代数学名著《孙子算经》中就记载了这样一道有趣的数学题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”你们知道这个古代数学问题的意思吗?
激发情感
这就是著名的“鸡兔同笼”问题。现在,大家用自己喜欢的方法来解决这个问题吧。
★用假设全是鸡或全是兔的方法来解,计算起来比较快。
★用列表的方法来解答。
★先假设鸡有17只,兔有18只,这样取中间两个数的假设比较快,接近答案。
激发情感
你们想知道古人是怎样解决这个问题的吗?
激发情感
有的同学不明白为什么“47﹣35=12”就是兔子的只数,谁能解释一下?
★ “94÷2=47”表示的是总脚数的一半。这时,一只鸡一只脚,即1个头有一只脚;一只兔2只脚,即1个头2只脚。所以脚数47比头数35多的47﹣35=12就是兔子的只数。
激发情感
94÷2=47
兔:47﹣35=12(只)
鸡:35﹣12=23(只)
古人这一思路新颖而奇特,这“抬腿法”也叫“减半法”,令古今中外数学家赞叹不已。这种解法给我们的启示是:思维方式一定要灵活多变,不能墨守成规。
激发情感
38名少先队员去划船,租了8条船,每条船都坐满人,大船能坐6人,小船能坐4人。这次活动租大船、小船各几条?
谁想来汇报一下自己小组的研究结果?
延伸应用
★这是一个“鸡兔同笼”问题,大船坐的人数较多,可以看作“兔”,而小船就看作“鸡”。
★大船当“兔”,坐的6人算作“兔脚”,小船当“鸡”,坐的4人算作“鸡脚”。问题就变成有38只脚(人),8个头(船数),每只兔(大船)有6只脚(人),每只鸡(小船)有4只脚(人),鸡、兔各有几只?
延伸应用
★假设全部是大船,8条船能坐6×8=48人,比实际38人多48﹣38=10人,因为每条大船比小船多坐6﹣4=2人,所以,有10÷2=5条小船,8﹣5=3条大船。
将“租船”问题转化成“鸡兔同笼”问题。
延伸应用
今天的学习有趣吗?大家有哪些收获?
“鸡兔同笼”问题是我国三大趣题之一。希望你们能用今天学到的方法去解决更多实际生活中的数学问题。
畅谈收获
感谢聆听!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
