苏教版 5下第3单元13 和与积的奇偶性微课课件(共30张PPT)
文档属性
| 名称 | 苏教版 5下第3单元13 和与积的奇偶性微课课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 10:12:07 | ||
图片预览








文档简介
(共30张PPT)
和与积的奇偶性
苏教版小学数学五年级(下册)
说说奇数和偶数各有什么特点?
奇数:个位上是1、3、5、7、或9。
偶数:个位上是2、4、6、8、或0。
数学小讲师
引入新知
交流预习成果:
1.几个不是0的自然数相加的和是奇数,还是偶数?有什么规律?
2.几个不是0的自然数相乘的积是奇数,还是偶数?有什么规律?
3.如何探究出这两个规律的?
探索规律
任务一:探究两个数和的奇偶性
举例:任意两个不是0的自然数相加
观察:我发现了
验证:
结论:
类型 加数 加数 和 和是奇数还是偶数
①
②
③
探索规律
研究小贴士:
(1)先独立思考,任意两个不是0的自然数相加,它们的和可能会有哪些情况。
(2)然后任意选两个不是0的自然数,求出它们的和,再看看和的奇偶性。
(3)接着观察表格,发现其中隐藏的规律,并举一些例子进行验证。
(4)最后写出你的结论。
探索规律
任务一:探究两个数和的奇偶性
举例:任意两个不是0的自然数相加
观察:我发现了
验证:
结论:
类型 加数 加数 和 和是奇数还是偶数
①
②
③
探索规律
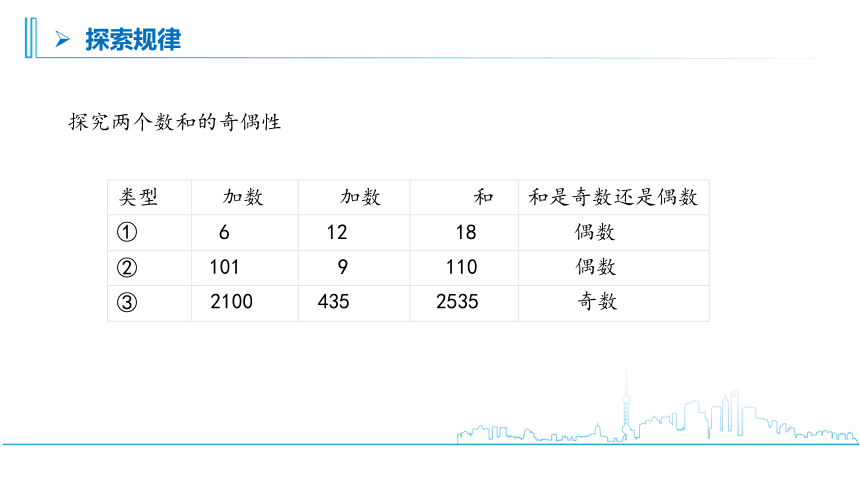
探究两个数和的奇偶性
类型 加数 加数 和 和是奇数还是偶数
①
②
③
6 12 18 偶数
101 9 110 偶数
2100 435 2535 奇数
探索规律
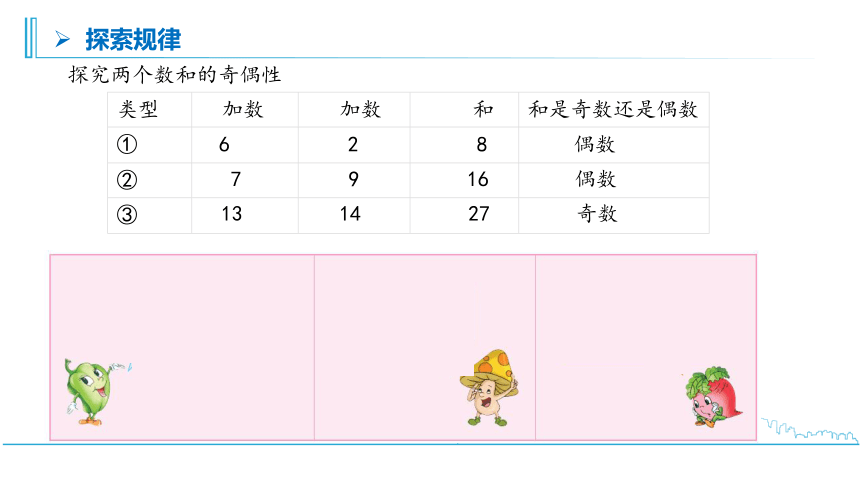
探究两个数和的奇偶性
类型 加数 加数 和 和是奇数还是偶数
①
②
③
6 2 8 偶数
7 9 16 偶数
13 14 27 奇数
探索规律
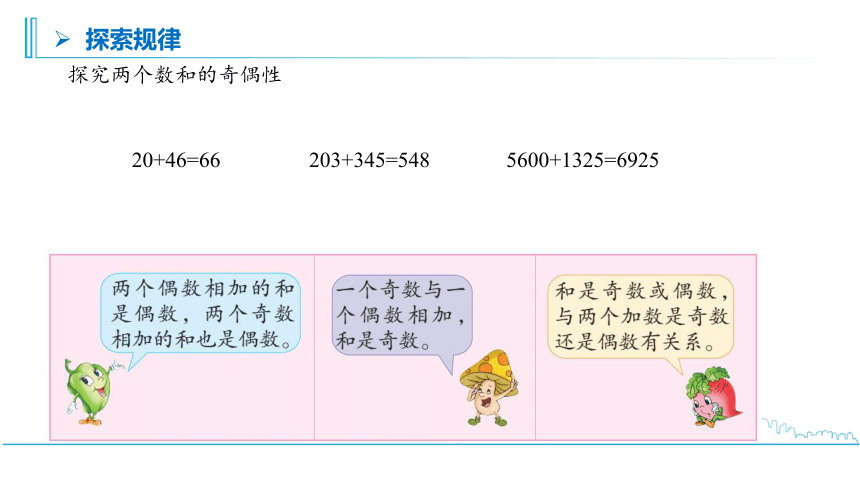
探究两个数和的奇偶性
20+46=66
203+345=548
5600+1325=6925
探索规律
结论:偶数+偶数=偶数
奇数+奇数=偶数
偶数+奇数=奇数
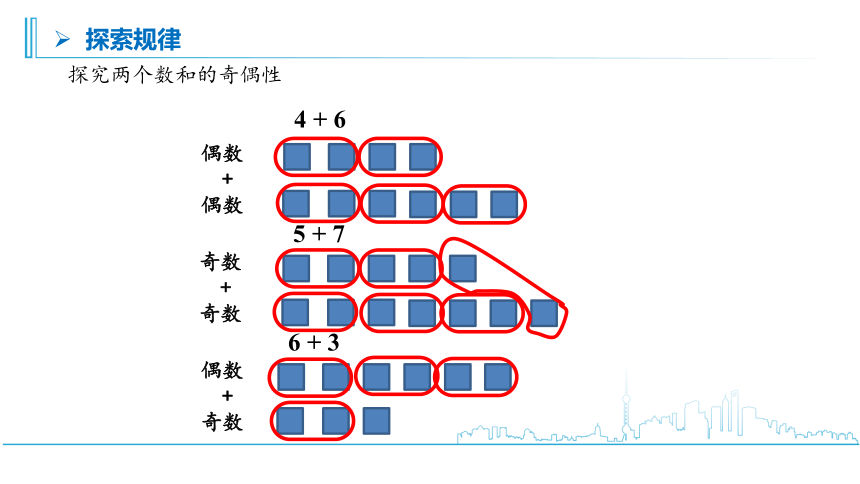
探究两个数和的奇偶性
4 + 6
偶数
+
偶数
5 + 7
奇数
+
奇数
6 + 3
偶数
+
奇数
探索规律
探究两个数和的奇偶性
探索规律
(3)打开数学书,左、右两边页码的和是奇数还是偶数?任意两个相邻自然数的和呢?你知道这是为什么吗? ( )
不计算,快速判断和的奇偶性。
(1)1357与2468的和 ( ) (2)2345与8767的和 ( )
探究两个数和的奇偶性
奇数
偶数
奇
偶
奇
奇
探索规律
探究两个数和的奇偶性
探索规律
(3)打开数学书,左、右两边页码的和是奇数还是偶数?任意两个相邻自然数的和呢?你知道这是为什么吗? ( )
不计算,快速判断和的奇偶性。
(1)1357与2468的和 ( ) (2)2345与8767的和 ( )
探究两个数和的奇偶性
奇数
偶数
奇
偶
奇
奇
50 + 51 = 101
偶数+奇数=奇数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19…
奇数
奇数
探索规律
任务二:探究几个数和的奇偶性
( )+( )+( )+( )…
举例
发现
验证
结论
解释
探索规律
任务二:探究几个数和的奇偶性
举例:任意几个不是0的自然数相加
观察:我写的连加算式中,有几个加数是偶数?有几个加数是奇数?
发现:和是奇数还是偶数,与加数中奇数的个数有什么关系?
验证:
结论:
类型 连 加 算 式 和 和是奇数还是偶数
①
②
③
探索规律
探究几个数和的奇偶性
类型 连 加 算 式 和 和是奇数还是偶数
① 2+8+4+20+12 46 偶 数
② 3+9+4+8+15+21+39 99 奇 数
③ 30+25+31+57+7+19+13+18 200 偶 数
探索规律
探究几个数和的奇偶性
类型 连 加 算 式 和 和是奇数还是偶数
① 2+8+4+20+12 46 偶 数
② 3+9+4+8+15+21+39 99 奇 数
③ 30+25+31+57+7+19+13+18+48 248 偶 数
加数中有1个、3个、5个……奇数时,和一定是奇数。
加数中有2个、4个、6个……奇数时,和一定是偶数。
探索规律
探究几个数和的奇偶性
加数中有1个、3个、5个……奇数时,和一定是奇数。
加数中有2个、4个、6个……奇数时,和一定是偶数。
验证:
4+8+7+5+10+1=35
203+46+84+20=353
27+54+43+82=206
77+45+121+387=630
59+76+65+89+91+3+171=554
和是偶数
和是奇数
探索规律
结论:几个不是0的自然数相加,当奇数的个数是奇数时,和是奇数;当奇数的个数是偶数时,和是偶数。
探究几个数和的奇偶性
4 + 6
偶数
+
偶数
+
偶数
+
偶数
.
.
.
.
.
.
+ 8
探索规律
探究几个数和的奇偶性
5 + 7
奇数
+
奇数
+
奇数
+ 9
+
奇数
.
.
.
.
.
.
探究几个数和的奇偶性
探索规律
偶数+ 偶数+偶数+……+奇数+奇数+奇数+……
如果算式中有奇数有偶数,和是奇数还是偶数呢?
偶数
奇数
偶数
探究几个数和的奇偶性
探索规律
奇数
偶数
拓展练习
1+3+5+…+29+30的和是奇数还是偶数?为什么?
探究几个数和的奇偶性
和是奇数,因为15个奇数的和是奇数。
1+2+3+4+5+6+7+8+9+10+11+12+13+14+…+29+30
1+2+3+4+5+6+7+8+9+10+11+12+13+14+…+29+30
探索规律
任务三:探究几个数积的奇偶性
举例:任意几个不是0的自然数相乘,积什么情况下是奇数?什么情况下是偶数?
观察:我发现了 。
验证:
结论: 。
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
1×3×5=15
8×4×10×2=640
1×8×3=24
3×5×7×6=630
探索规律
探究几个数积的奇偶性
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
探索规律
探究几个数积的奇偶性
7×23×15=2415
7×23×15×2=4830
20×4×29×18=41760
验证:
15×6×9×13=10530
探索规律
探究几个数积的奇偶性
结论:乘数中有偶数的乘法算式,积就是偶数;乘数中没有偶数的乘法算式,积就是奇数。
关键:找偶数
3×5×7×6=630
1×3×5=15
630是偶数6的倍数,也一定是2的倍数,所以积是偶数。
15的因数都是奇数,它不可能是2的倍数,所以积是奇数。
多写一些算式,并进行比较,才能发现规律。
要注意从不同的算式中发现共同的特点。
举例和验证是发现规律的好方法。
回顾反思
回顾探索和发现规律的过程,说说自己的体会。
举例
发现
验证
结论
解释
再 见 !
和与积的奇偶性
苏教版小学数学五年级(下册)
说说奇数和偶数各有什么特点?
奇数:个位上是1、3、5、7、或9。
偶数:个位上是2、4、6、8、或0。
数学小讲师
引入新知
交流预习成果:
1.几个不是0的自然数相加的和是奇数,还是偶数?有什么规律?
2.几个不是0的自然数相乘的积是奇数,还是偶数?有什么规律?
3.如何探究出这两个规律的?
探索规律
任务一:探究两个数和的奇偶性
举例:任意两个不是0的自然数相加
观察:我发现了
验证:
结论:
类型 加数 加数 和 和是奇数还是偶数
①
②
③
探索规律
研究小贴士:
(1)先独立思考,任意两个不是0的自然数相加,它们的和可能会有哪些情况。
(2)然后任意选两个不是0的自然数,求出它们的和,再看看和的奇偶性。
(3)接着观察表格,发现其中隐藏的规律,并举一些例子进行验证。
(4)最后写出你的结论。
探索规律
任务一:探究两个数和的奇偶性
举例:任意两个不是0的自然数相加
观察:我发现了
验证:
结论:
类型 加数 加数 和 和是奇数还是偶数
①
②
③
探索规律
探究两个数和的奇偶性
类型 加数 加数 和 和是奇数还是偶数
①
②
③
6 12 18 偶数
101 9 110 偶数
2100 435 2535 奇数
探索规律
探究两个数和的奇偶性
类型 加数 加数 和 和是奇数还是偶数
①
②
③
6 2 8 偶数
7 9 16 偶数
13 14 27 奇数
探索规律
探究两个数和的奇偶性
20+46=66
203+345=548
5600+1325=6925
探索规律
结论:偶数+偶数=偶数
奇数+奇数=偶数
偶数+奇数=奇数
探究两个数和的奇偶性
4 + 6
偶数
+
偶数
5 + 7
奇数
+
奇数
6 + 3
偶数
+
奇数
探索规律
探究两个数和的奇偶性
探索规律
(3)打开数学书,左、右两边页码的和是奇数还是偶数?任意两个相邻自然数的和呢?你知道这是为什么吗? ( )
不计算,快速判断和的奇偶性。
(1)1357与2468的和 ( ) (2)2345与8767的和 ( )
探究两个数和的奇偶性
奇数
偶数
奇
偶
奇
奇
探索规律
探究两个数和的奇偶性
探索规律
(3)打开数学书,左、右两边页码的和是奇数还是偶数?任意两个相邻自然数的和呢?你知道这是为什么吗? ( )
不计算,快速判断和的奇偶性。
(1)1357与2468的和 ( ) (2)2345与8767的和 ( )
探究两个数和的奇偶性
奇数
偶数
奇
偶
奇
奇
50 + 51 = 101
偶数+奇数=奇数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19…
奇数
奇数
探索规律
任务二:探究几个数和的奇偶性
( )+( )+( )+( )…
举例
发现
验证
结论
解释
探索规律
任务二:探究几个数和的奇偶性
举例:任意几个不是0的自然数相加
观察:我写的连加算式中,有几个加数是偶数?有几个加数是奇数?
发现:和是奇数还是偶数,与加数中奇数的个数有什么关系?
验证:
结论:
类型 连 加 算 式 和 和是奇数还是偶数
①
②
③
探索规律
探究几个数和的奇偶性
类型 连 加 算 式 和 和是奇数还是偶数
① 2+8+4+20+12 46 偶 数
② 3+9+4+8+15+21+39 99 奇 数
③ 30+25+31+57+7+19+13+18 200 偶 数
探索规律
探究几个数和的奇偶性
类型 连 加 算 式 和 和是奇数还是偶数
① 2+8+4+20+12 46 偶 数
② 3+9+4+8+15+21+39 99 奇 数
③ 30+25+31+57+7+19+13+18+48 248 偶 数
加数中有1个、3个、5个……奇数时,和一定是奇数。
加数中有2个、4个、6个……奇数时,和一定是偶数。
探索规律
探究几个数和的奇偶性
加数中有1个、3个、5个……奇数时,和一定是奇数。
加数中有2个、4个、6个……奇数时,和一定是偶数。
验证:
4+8+7+5+10+1=35
203+46+84+20=353
27+54+43+82=206
77+45+121+387=630
59+76+65+89+91+3+171=554
和是偶数
和是奇数
探索规律
结论:几个不是0的自然数相加,当奇数的个数是奇数时,和是奇数;当奇数的个数是偶数时,和是偶数。
探究几个数和的奇偶性
4 + 6
偶数
+
偶数
+
偶数
+
偶数
.
.
.
.
.
.
+ 8
探索规律
探究几个数和的奇偶性
5 + 7
奇数
+
奇数
+
奇数
+ 9
+
奇数
.
.
.
.
.
.
探究几个数和的奇偶性
探索规律
偶数+ 偶数+偶数+……+奇数+奇数+奇数+……
如果算式中有奇数有偶数,和是奇数还是偶数呢?
偶数
奇数
偶数
探究几个数和的奇偶性
探索规律
奇数
偶数
拓展练习
1+3+5+…+29+30的和是奇数还是偶数?为什么?
探究几个数和的奇偶性
和是奇数,因为15个奇数的和是奇数。
1+2+3+4+5+6+7+8+9+10+11+12+13+14+…+29+30
1+2+3+4+5+6+7+8+9+10+11+12+13+14+…+29+30
探索规律
任务三:探究几个数积的奇偶性
举例:任意几个不是0的自然数相乘,积什么情况下是奇数?什么情况下是偶数?
观察:我发现了 。
验证:
结论: 。
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
1×3×5=15
8×4×10×2=640
1×8×3=24
3×5×7×6=630
探索规律
探究几个数积的奇偶性
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
探索规律
探究几个数积的奇偶性
7×23×15=2415
7×23×15×2=4830
20×4×29×18=41760
验证:
15×6×9×13=10530
探索规律
探究几个数积的奇偶性
结论:乘数中有偶数的乘法算式,积就是偶数;乘数中没有偶数的乘法算式,积就是奇数。
关键:找偶数
3×5×7×6=630
1×3×5=15
630是偶数6的倍数,也一定是2的倍数,所以积是偶数。
15的因数都是奇数,它不可能是2的倍数,所以积是奇数。
多写一些算式,并进行比较,才能发现规律。
要注意从不同的算式中发现共同的特点。
举例和验证是发现规律的好方法。
回顾反思
回顾探索和发现规律的过程,说说自己的体会。
举例
发现
验证
结论
解释
再 见 !
