7.1.2全概率公式 课件(共21张PPT)
文档属性
| 名称 | 7.1.2全概率公式 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 11:09:21 | ||
图片预览







文档简介
(共21张PPT)
7.1.2全概率公式
X
1.了解全概率公式及其推导过程
重点
知识目标
2.全概率公式及其应用
教学目标⊙
结合古典概型,会利用全概率公式求事件的概率
难点
核心素养
通过数学抽象得出一般性的数学结论,
培养学生的数学抽象素养
复习回顾
1.条件概率:在事件A发生的条件下,事件发生的概率称为条件概率,即
P(AB)
P(B A)=
P(A)
2.概率的乘法公式:
由条件概率公式可得
P(AB)=P(A)P(B A).
3.概率的加法公式:
如事件B,C互斥,则有
P(BUCA)=P(B A)+P(C A).
情境
导入
从有α个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球不
再放回.显然,第1次摸到红球的概率为,邦么第2次摸到红球的概器
是多大?如何计算这个概率呢?
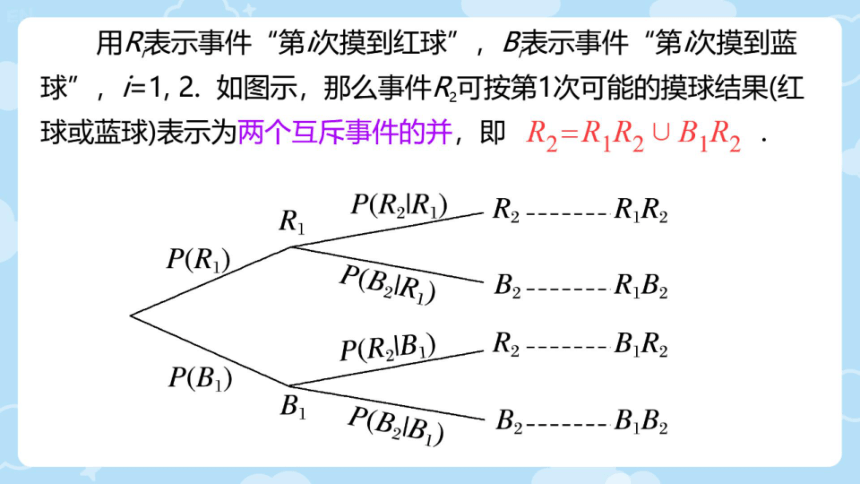
用R表示事件“第次摸到红球”,B表示事件“"第次摸到蓝
球”,仁1,2.如图示,那么事件R可按第1次可能的摸球结果(红
球或蓝球)表示为两个互斥事件的并,即R2=RR2UB1R2·
R
P(R2lR)一R2--RR2
P(R)
P(B2IR)
B2---R1B2
P(R2IB)
R2--BR2
P(B)
P(B2IB
B2---B1B2
利用概率的加法公式和乘法公式,得
P(R,)=P(R R2UB R2)=P(R R2)+P(B R2)
=P(R)P(R,R)+P(B)P(R2 B
a-1
b
L
a+b a+b-1
a+b a+b-1
L
上述过程采用的方法是:按照某种标准,将一
a+b
个复杂事件表示为两个互斥事件的并,再由概率
的加法公式和乘法公式求得这个复杂事件的概率.
讲授新课
上述过程采用的方法是:按照某种标准,将一个复杂事件表示
为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂
事件的概率.
全概率公式:
一般地,设A1,A2,,An是一组两两互斥的事件,AUA,UUAn=2,且
P(A)>0,i=1,2,,n,则对任意的事件B∈2,有
我们称上面的公式为全概率
P(B=∑P(A4,)P(BIA,.
公式.全概率公式是概率论中最
i-
基本的公式之一.
对全概率公式的理解
某一事件B的发生可能有各种的原因,如果B是由原因A(=1,2,,n)(A,两两
互斥,构成一个完备事件)所引起,则B发生的概率是P(BA)=P(A)P(BA),
每一原因都可能导致B发生,故B发生的概率是各原因A引
起,BA(=1,2,,n)发生概率的总和,即全概率公式,
由此可以形象地把全概率公式看成为“由原因求结果”,每个原因对结果的
发生有一定的“作用”,即结果发生的可能性与各种原因的“作用”大小有关
7.1.2全概率公式
X
1.了解全概率公式及其推导过程
重点
知识目标
2.全概率公式及其应用
教学目标⊙
结合古典概型,会利用全概率公式求事件的概率
难点
核心素养
通过数学抽象得出一般性的数学结论,
培养学生的数学抽象素养
复习回顾
1.条件概率:在事件A发生的条件下,事件发生的概率称为条件概率,即
P(AB)
P(B A)=
P(A)
2.概率的乘法公式:
由条件概率公式可得
P(AB)=P(A)P(B A).
3.概率的加法公式:
如事件B,C互斥,则有
P(BUCA)=P(B A)+P(C A).
情境
导入
从有α个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球不
再放回.显然,第1次摸到红球的概率为,邦么第2次摸到红球的概器
是多大?如何计算这个概率呢?
用R表示事件“第次摸到红球”,B表示事件“"第次摸到蓝
球”,仁1,2.如图示,那么事件R可按第1次可能的摸球结果(红
球或蓝球)表示为两个互斥事件的并,即R2=RR2UB1R2·
R
P(R2lR)一R2--RR2
P(R)
P(B2IR)
B2---R1B2
P(R2IB)
R2--BR2
P(B)
P(B2IB
B2---B1B2
利用概率的加法公式和乘法公式,得
P(R,)=P(R R2UB R2)=P(R R2)+P(B R2)
=P(R)P(R,R)+P(B)P(R2 B
a-1
b
L
a+b a+b-1
a+b a+b-1
L
上述过程采用的方法是:按照某种标准,将一
a+b
个复杂事件表示为两个互斥事件的并,再由概率
的加法公式和乘法公式求得这个复杂事件的概率.
讲授新课
上述过程采用的方法是:按照某种标准,将一个复杂事件表示
为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂
事件的概率.
全概率公式:
一般地,设A1,A2,,An是一组两两互斥的事件,AUA,UUAn=2,且
P(A)>0,i=1,2,,n,则对任意的事件B∈2,有
我们称上面的公式为全概率
P(B=∑P(A4,)P(BIA,.
公式.全概率公式是概率论中最
i-
基本的公式之一.
对全概率公式的理解
某一事件B的发生可能有各种的原因,如果B是由原因A(=1,2,,n)(A,两两
互斥,构成一个完备事件)所引起,则B发生的概率是P(BA)=P(A)P(BA),
每一原因都可能导致B发生,故B发生的概率是各原因A引
起,BA(=1,2,,n)发生概率的总和,即全概率公式,
由此可以形象地把全概率公式看成为“由原因求结果”,每个原因对结果的
发生有一定的“作用”,即结果发生的可能性与各种原因的“作用”大小有关
