高二下学期数学人教A版选修2-3 1.1分类加法计数原理与分步乘法计数原理 第一课时 课件(18张PPT)
文档属性
| 名称 | 高二下学期数学人教A版选修2-3 1.1分类加法计数原理与分步乘法计数原理 第一课时 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 11:10:29 | ||
图片预览






文档简介
(共18张PPT)
1.1 分类加法计数原理与分步乘法计数原理
赤峰
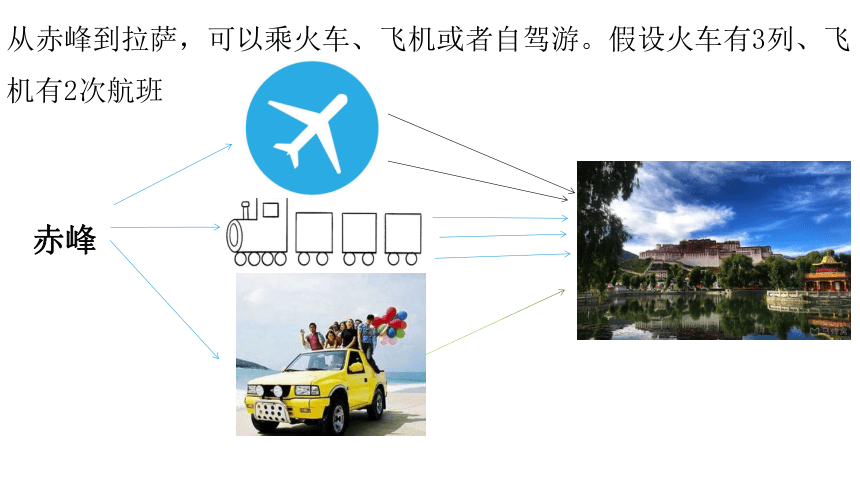
从赤峰到拉萨,可以乘火车、飞机或者自驾游。假设火车有3列、飞机有2次航班
一、分类加法计数原理
2
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法。
判断:
1. 在分类加法计数原理中,两类不同方案中的方法可以相同( )
2. 在分类加法计数原理中,每类方案中的方法都能完成这件事( )
X
√
例题1
3
一个口袋里有5封信,另一个口袋里有4封信,各封信的内容均不相同,从口袋取一封信,有多少种不同的取法?
第一类:从第一个口袋里取一封信,有5种不同方法;
第二类:从第二个口袋里取一封信,有4种不同方法;
共有5+4=9种不同方法。
训练1
4
高二(15)班有学生50人,男生30人;高二(16)班有学生60人,女生30人;高二(17)班有学生55人,男生35人。
(1)从中选一名学生任学生会主席,有多少种不同的选法?
(2)从高二(15)班、(16)班男生中或从高二(17)班女生中选一名学生任体育部部长,有多少种不同选法?
4
5
赤峰
郑州
拉萨
同学A从赤峰到拉萨,选择坐飞机,需在郑州中转,已知赤峰的玉龙机场到郑州有2次航班,郑州到拉萨的贡嘎机场有3次航班
同学A从赤峰到拉萨可以有多少种选择?
5
用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,...,B1,B2,...的方式给教室里的座位编号,总共能编出多少个不同的号码?
二、分步乘法计数原理
6
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有N=m×n种不同方法。
1.在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的( )
2.在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事( )
√
×
例题2
7
4
例题3
8
书架的第一层放有6本不同的数学书,第二层放有6本不同的语文书,第三层放有5本不同的英语书。
(1)从书架的中任取一本数学、一本语文和一本英语共三本书不同取法有多少种?
(2)从这些书中任取三本,并且在书架上按次序排好,有多少种不同的排法?
4
例题4
9
用0,1,2,3,4五个数字,
(1)可以排出多少个三位数字的电话号码?
(2)可以排成多少个三位数?
(3)可以排成多少个能被2整除的无重复数字的三位数?
归纳小结
11
分类加法与分步乘法计数原理的区别和联系
共同点
区别
有关完成一件事情的不同方法的种数的问题。
分类计数原理:方法相互独立,每种方法均能
独立完成这件事.
分步计数原理:各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事.
D
A
谢 谢 !
授课教师:宋亚飞
1.1 分类加法计数原理与分步乘法计数原理
赤峰
从赤峰到拉萨,可以乘火车、飞机或者自驾游。假设火车有3列、飞机有2次航班
一、分类加法计数原理
2
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法。
判断:
1. 在分类加法计数原理中,两类不同方案中的方法可以相同( )
2. 在分类加法计数原理中,每类方案中的方法都能完成这件事( )
X
√
例题1
3
一个口袋里有5封信,另一个口袋里有4封信,各封信的内容均不相同,从口袋取一封信,有多少种不同的取法?
第一类:从第一个口袋里取一封信,有5种不同方法;
第二类:从第二个口袋里取一封信,有4种不同方法;
共有5+4=9种不同方法。
训练1
4
高二(15)班有学生50人,男生30人;高二(16)班有学生60人,女生30人;高二(17)班有学生55人,男生35人。
(1)从中选一名学生任学生会主席,有多少种不同的选法?
(2)从高二(15)班、(16)班男生中或从高二(17)班女生中选一名学生任体育部部长,有多少种不同选法?
4
5
赤峰
郑州
拉萨
同学A从赤峰到拉萨,选择坐飞机,需在郑州中转,已知赤峰的玉龙机场到郑州有2次航班,郑州到拉萨的贡嘎机场有3次航班
同学A从赤峰到拉萨可以有多少种选择?
5
用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,...,B1,B2,...的方式给教室里的座位编号,总共能编出多少个不同的号码?
二、分步乘法计数原理
6
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有N=m×n种不同方法。
1.在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的( )
2.在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事( )
√
×
例题2
7
4
例题3
8
书架的第一层放有6本不同的数学书,第二层放有6本不同的语文书,第三层放有5本不同的英语书。
(1)从书架的中任取一本数学、一本语文和一本英语共三本书不同取法有多少种?
(2)从这些书中任取三本,并且在书架上按次序排好,有多少种不同的排法?
4
例题4
9
用0,1,2,3,4五个数字,
(1)可以排出多少个三位数字的电话号码?
(2)可以排成多少个三位数?
(3)可以排成多少个能被2整除的无重复数字的三位数?
归纳小结
11
分类加法与分步乘法计数原理的区别和联系
共同点
区别
有关完成一件事情的不同方法的种数的问题。
分类计数原理:方法相互独立,每种方法均能
独立完成这件事.
分步计数原理:各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事.
D
A
谢 谢 !
授课教师:宋亚飞
