高二上学期数学人教B版(2019)选择性必修第二册3.1.1基本计数原理 课件(27张PPT)
文档属性
| 名称 | 高二上学期数学人教B版(2019)选择性必修第二册3.1.1基本计数原理 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 11:15:06 | ||
图片预览







文档简介
(共27张PPT)
第三章 排列、组合与二项式定理
3.1.1 基本计数原理
学习目标
1.了解分类加法计数原理、分步乘法计数原理及其意义.
2.能准确应用两个计数原理解决一些简单的实际问题.
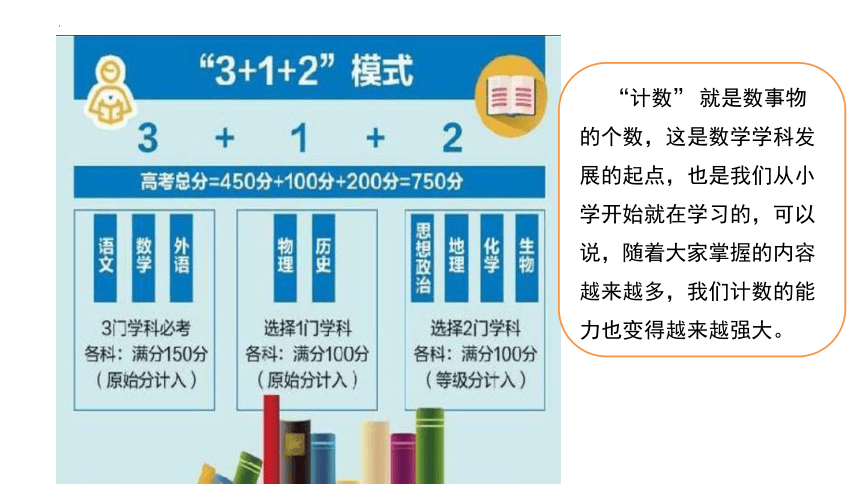
“计数” 就是数事物的个数,这是数学学科发展的起点,也是我们从小学开始就在学习的,可以说,随着大家掌握的内容越来越多,我们计数的能力也变得越来越强大。
第三章 排列、组合与二项式定理
3.1.1 基本计数原理
学习目标
1.了解分类加法计数原理、分步乘法计数原理及其意义.
2.能准确应用两个计数原理解决一些简单的实际问题.
习水县第五中学 蔡玉珍 2023年2月
情景与问题
数学学习和日常生活中,我们经常会遇到类似“共有多少种情况” 的计数问题,例如:
(1)集合共有多少个不同的子集?
(2)由3个数组成的密码锁,如图所示,如果忘记了密码,
最多要试多少次才能打开密码锁?
(3)有4位同学和一位老师站成一排照相,如果老师要站在正中间,如图所示,有多少种不同的站法?
你能解答这些问题吗?
你能解答下述两个问题吗?试着由此归纳出一般的规律。
(1)已知某天从北京到上海G字头列车有43班,D字头列车有2班,其他列车有3班,小张想这一天坐火车从北京到上海去旅游,不考虑其他因素,小张有多少种不同的选择?
(2)从甲地到乙地可以乘火车,也可以乘汽车,还可以乘轮船,假定火车每日有1班,汽车每日有3班,轮船每日有2班,那么一天中从甲地到乙地有多少种不同的走法呢?
尝试与发现
一、分类加法计数原理
完成一件事,如果有类办法,且:第一类办法中有种不同的方法,第二类办法中有种不同的方法……第类办法中有种不同的方法,那么完成这件事共有种不同的方法.
1.某学生去书店,发现两本好书,决定至少买其中一本,其购买方法共有( )
A.1种 B.2种 C.3种 D.4种
解析:有两类不同的办法:买一本或两本,各类购买方法依次有2种或1种,故购买方法共有2+1=3种.故选C.
答案:C
巩固体悟
2.在所有的两位数中,个位数字大于十位数字的两位数共有多少个
巩固体悟
解法一:按十位上的数字分别是1,2,3,4,5,6,7,8,分成8类.在每一类中满足条件的两位数分别有8个、7个、6个、5个、4个、3个、2个、1个.由分类加法计数原理知,满足条件的两位数共有8+7+6+5+4+3+2+1=36(个).
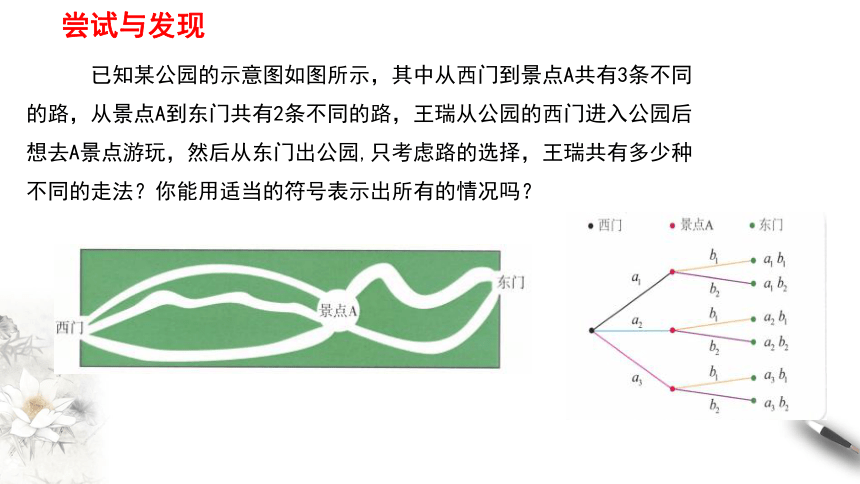
已知某公园的示意图如图所示,其中从西门到景点A共有3条不同的路,从景点A到东门共有2条不同的路,王瑞从公园的西门进入公园后想去A景点游玩,然后从东门出公园,只考虑路的选择,王瑞共有多少种不同的走法?你能用适当的符号表示出所有的情况吗?
尝试与发现
二、分步乘法计数原理
完成一件事,如果需要分成个步骤,且:做第一步有种不同的方法,做第二步有种不同的方法……做第步有种不同的方法,那么完成这件事共有种不同的方法。
一、分类加法计数原理
完成一件事,如果有类办法,且:第一类办法中有种不同的方法,第二类办法中有种不同的方法……第类办法中有种不同的方法,那么完成这件事共有种不同的方法.
二、分步乘法计数原理
完成一件事,如果需要分成个步骤,且:做第一步有种不同的方法,做第二步有种不同的方法……做第步有种不同的方法,那么完成这件事共有种不同的方法。
2.区别
分类加法计数原理 分步乘法计数原理
区别一 完成一件事共有n类办法,关键词是“分类” 完成一件事共有n个步骤,关键词是“分步”
区别二 每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事 除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三 各类办法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
两个原理的联系与区别
1.联系:分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.
1.一个袋子里装有7张不同的中国移动手机卡,另一个袋子里装有8张不同的中国联通手机卡,某人想得到一张中国移动卡和一张中国联通卡,供自己今后使用,则不同的取法种数为( )
A.78 B.15 C.87 D.56
解析:由分步乘法计数原理知,有7×8=56种不同的取法.
答案:D
巩固体悟
由4个数组成的密码锁,如图所示,如果忘记了密码,最多要试多少次才能打开密码锁?
最多试 次
回归情景与问题
10种
10种
10种
10种
有6位同学和一位老师站成一排照相,如果老师要站在正中间,如图所示,有多少种不同的站法?
老师
不妨从左起第一个位置开始,逐步确定各个位置上的人选,需分四步完成:
5种
4种
3种
2种
根据分步乘法计数原理:共种.
这种方法我们是从位置入手,分步完成.
回归情景与问题
6种
1种
典例解析
范例引领
例1.用1,2,3,4,5可以排成多少个数字不重复的三位数?
分别指定这个三位数的百位、十位、个位上的
数字,因此可以分为三步完成:
百
十
个
3种
5种
第一步:确定百位上的数字,共5种方法;
4种
第二步:确定十位上的数字,共4种方法;
第三步:确定个位上的数字,共3种方法;
根据分步乘法计数原理:
共有个三位数.
变式1:用0,1,2,3,4可以排成多少个三位数?
拓展衍生
变式2:用0,1,9这10个数字,可以排成多少个有重复的三位数?
解析:根据分步乘法计数原理0,1,2,3,4共能组成4×4×3=48(个)三位数.
解析:根据分步乘法计数原理,0,1,2,…,9共能组成9×10×10900(个)三位数,其中无重复数字的三位数有9×9×8=648(个),所以有重复数字的三位数有900-648=252(个).
例2. 在某设计活动中,李明要用红色和蓝色填涂四个格子如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
范例引领
优点:事件的结果可以直观的一一列举出来
不妨设:红色为R,蓝色为B.
列举法:RRBB,RBRB,RBBR,BRRB,BRBR,BBRR,共6种.
当问题比较复杂,出现的结果比较多时,为了避免出
现列举重复或者遗漏,通常我们在列举过程中对事情
可能发生的结果“分类”,以此达到简化问题,提高
准确率的目的.
R
法1:从格子的位置入手,对第一个格子的颜色分类(R、B两类):
RRBB,
RBRB,
RBBR,共3种
第一类,第一个格子为R
R
B
B
B
R
B
B
R
从位置出发,顺次讨论填涂的颜色
第二类,第一个格子为B:
BRRB,
BRBR,
BBRR,共3种
根据分类加法计数原理:共有3+3=6种
B
R
B
R
B
B
R
R
R
试想想,我们是否还有其他的列举方法
法2:按照同一颜色的格子是否相邻分类(不妨讨论红色):
第一类,相邻 第二类,不相邻
R
R
R
R
R
R
RRBB
BRRB
BBRR
3种
R
R
R
R
R
R
RBRB
BRBR
RBBR
3种
根据分类加法计数原理:共有3+3=6种
分类的方法:
1.位置(按格子的位置顺次讨论);
2.元素之间的位置关系(同一颜色是否相邻
变式1:如图所示,将红、黄、蓝、白、黑五种颜色涂在这“田”字形计的4个小方格内,每格涂一种颜色,如果颜色不能反复使用,共有多少种不同的涂色方法?
解:
①第1个小方格可以从5种颜色中任取一种颜色涂上,有5种不同的涂法,
②第2个小方格可以从剩下4种颜色中任取一种颜色涂上,有4种不同的涂法,
③第3个小方格可以从剩下3种颜色中任取一种颜色涂上,有3种不同的涂法,
④第4个小方格可以从剩下2种颜色中任取一种颜色涂上,有2种不同的涂法,
由分步乘法计数原理可得共有5(种)不同的涂法.
1 2
3 4
拓展衍生
变式2:如图所示,将红、黄、蓝、白、黑五种颜色涂在这“田”字形计的4个小方格内,每格涂一种颜色,相邻两格的涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
解:第1个小方格可以分5种颜色中任取一种颜色涂上,有5种不同的涂法。
①当第2个、第3个小方格涂不同颜色时,有4×3=12种不同的涂法,第4个小方格有3种不同的涂法,由分步乘法计数原理可知有5×12×3=180(种)不同的涂法.
②当第2个、第3个小方格涂相同颜色时,有4种涂法,由于相邻两格不同色,因此,第4个小方格也有4种不同的涂法,由分步乘法计数原理可知有5×4×4=80(种)不同的涂法.
由分类加法计数原理可得共有180+80=260(种)不同的涂法.
拓展衍生
1 2
3 4
课堂小结
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
归纳总结
利用分步乘法计数原理解题的一般思路
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
【课后作业】
教材 8页 A组1,2,3,4
教材 8页 B组1,2
第三章 排列、组合与二项式定理
3.1.1 基本计数原理
学习目标
1.了解分类加法计数原理、分步乘法计数原理及其意义.
2.能准确应用两个计数原理解决一些简单的实际问题.
“计数” 就是数事物的个数,这是数学学科发展的起点,也是我们从小学开始就在学习的,可以说,随着大家掌握的内容越来越多,我们计数的能力也变得越来越强大。
第三章 排列、组合与二项式定理
3.1.1 基本计数原理
学习目标
1.了解分类加法计数原理、分步乘法计数原理及其意义.
2.能准确应用两个计数原理解决一些简单的实际问题.
习水县第五中学 蔡玉珍 2023年2月
情景与问题
数学学习和日常生活中,我们经常会遇到类似“共有多少种情况” 的计数问题,例如:
(1)集合共有多少个不同的子集?
(2)由3个数组成的密码锁,如图所示,如果忘记了密码,
最多要试多少次才能打开密码锁?
(3)有4位同学和一位老师站成一排照相,如果老师要站在正中间,如图所示,有多少种不同的站法?
你能解答这些问题吗?
你能解答下述两个问题吗?试着由此归纳出一般的规律。
(1)已知某天从北京到上海G字头列车有43班,D字头列车有2班,其他列车有3班,小张想这一天坐火车从北京到上海去旅游,不考虑其他因素,小张有多少种不同的选择?
(2)从甲地到乙地可以乘火车,也可以乘汽车,还可以乘轮船,假定火车每日有1班,汽车每日有3班,轮船每日有2班,那么一天中从甲地到乙地有多少种不同的走法呢?
尝试与发现
一、分类加法计数原理
完成一件事,如果有类办法,且:第一类办法中有种不同的方法,第二类办法中有种不同的方法……第类办法中有种不同的方法,那么完成这件事共有种不同的方法.
1.某学生去书店,发现两本好书,决定至少买其中一本,其购买方法共有( )
A.1种 B.2种 C.3种 D.4种
解析:有两类不同的办法:买一本或两本,各类购买方法依次有2种或1种,故购买方法共有2+1=3种.故选C.
答案:C
巩固体悟
2.在所有的两位数中,个位数字大于十位数字的两位数共有多少个
巩固体悟
解法一:按十位上的数字分别是1,2,3,4,5,6,7,8,分成8类.在每一类中满足条件的两位数分别有8个、7个、6个、5个、4个、3个、2个、1个.由分类加法计数原理知,满足条件的两位数共有8+7+6+5+4+3+2+1=36(个).
已知某公园的示意图如图所示,其中从西门到景点A共有3条不同的路,从景点A到东门共有2条不同的路,王瑞从公园的西门进入公园后想去A景点游玩,然后从东门出公园,只考虑路的选择,王瑞共有多少种不同的走法?你能用适当的符号表示出所有的情况吗?
尝试与发现
二、分步乘法计数原理
完成一件事,如果需要分成个步骤,且:做第一步有种不同的方法,做第二步有种不同的方法……做第步有种不同的方法,那么完成这件事共有种不同的方法。
一、分类加法计数原理
完成一件事,如果有类办法,且:第一类办法中有种不同的方法,第二类办法中有种不同的方法……第类办法中有种不同的方法,那么完成这件事共有种不同的方法.
二、分步乘法计数原理
完成一件事,如果需要分成个步骤,且:做第一步有种不同的方法,做第二步有种不同的方法……做第步有种不同的方法,那么完成这件事共有种不同的方法。
2.区别
分类加法计数原理 分步乘法计数原理
区别一 完成一件事共有n类办法,关键词是“分类” 完成一件事共有n个步骤,关键词是“分步”
区别二 每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事 除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三 各类办法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
两个原理的联系与区别
1.联系:分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.
1.一个袋子里装有7张不同的中国移动手机卡,另一个袋子里装有8张不同的中国联通手机卡,某人想得到一张中国移动卡和一张中国联通卡,供自己今后使用,则不同的取法种数为( )
A.78 B.15 C.87 D.56
解析:由分步乘法计数原理知,有7×8=56种不同的取法.
答案:D
巩固体悟
由4个数组成的密码锁,如图所示,如果忘记了密码,最多要试多少次才能打开密码锁?
最多试 次
回归情景与问题
10种
10种
10种
10种
有6位同学和一位老师站成一排照相,如果老师要站在正中间,如图所示,有多少种不同的站法?
老师
不妨从左起第一个位置开始,逐步确定各个位置上的人选,需分四步完成:
5种
4种
3种
2种
根据分步乘法计数原理:共种.
这种方法我们是从位置入手,分步完成.
回归情景与问题
6种
1种
典例解析
范例引领
例1.用1,2,3,4,5可以排成多少个数字不重复的三位数?
分别指定这个三位数的百位、十位、个位上的
数字,因此可以分为三步完成:
百
十
个
3种
5种
第一步:确定百位上的数字,共5种方法;
4种
第二步:确定十位上的数字,共4种方法;
第三步:确定个位上的数字,共3种方法;
根据分步乘法计数原理:
共有个三位数.
变式1:用0,1,2,3,4可以排成多少个三位数?
拓展衍生
变式2:用0,1,9这10个数字,可以排成多少个有重复的三位数?
解析:根据分步乘法计数原理0,1,2,3,4共能组成4×4×3=48(个)三位数.
解析:根据分步乘法计数原理,0,1,2,…,9共能组成9×10×10900(个)三位数,其中无重复数字的三位数有9×9×8=648(个),所以有重复数字的三位数有900-648=252(个).
例2. 在某设计活动中,李明要用红色和蓝色填涂四个格子如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
范例引领
优点:事件的结果可以直观的一一列举出来
不妨设:红色为R,蓝色为B.
列举法:RRBB,RBRB,RBBR,BRRB,BRBR,BBRR,共6种.
当问题比较复杂,出现的结果比较多时,为了避免出
现列举重复或者遗漏,通常我们在列举过程中对事情
可能发生的结果“分类”,以此达到简化问题,提高
准确率的目的.
R
法1:从格子的位置入手,对第一个格子的颜色分类(R、B两类):
RRBB,
RBRB,
RBBR,共3种
第一类,第一个格子为R
R
B
B
B
R
B
B
R
从位置出发,顺次讨论填涂的颜色
第二类,第一个格子为B:
BRRB,
BRBR,
BBRR,共3种
根据分类加法计数原理:共有3+3=6种
B
R
B
R
B
B
R
R
R
试想想,我们是否还有其他的列举方法
法2:按照同一颜色的格子是否相邻分类(不妨讨论红色):
第一类,相邻 第二类,不相邻
R
R
R
R
R
R
RRBB
BRRB
BBRR
3种
R
R
R
R
R
R
RBRB
BRBR
RBBR
3种
根据分类加法计数原理:共有3+3=6种
分类的方法:
1.位置(按格子的位置顺次讨论);
2.元素之间的位置关系(同一颜色是否相邻
变式1:如图所示,将红、黄、蓝、白、黑五种颜色涂在这“田”字形计的4个小方格内,每格涂一种颜色,如果颜色不能反复使用,共有多少种不同的涂色方法?
解:
①第1个小方格可以从5种颜色中任取一种颜色涂上,有5种不同的涂法,
②第2个小方格可以从剩下4种颜色中任取一种颜色涂上,有4种不同的涂法,
③第3个小方格可以从剩下3种颜色中任取一种颜色涂上,有3种不同的涂法,
④第4个小方格可以从剩下2种颜色中任取一种颜色涂上,有2种不同的涂法,
由分步乘法计数原理可得共有5(种)不同的涂法.
1 2
3 4
拓展衍生
变式2:如图所示,将红、黄、蓝、白、黑五种颜色涂在这“田”字形计的4个小方格内,每格涂一种颜色,相邻两格的涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
解:第1个小方格可以分5种颜色中任取一种颜色涂上,有5种不同的涂法。
①当第2个、第3个小方格涂不同颜色时,有4×3=12种不同的涂法,第4个小方格有3种不同的涂法,由分步乘法计数原理可知有5×12×3=180(种)不同的涂法.
②当第2个、第3个小方格涂相同颜色时,有4种涂法,由于相邻两格不同色,因此,第4个小方格也有4种不同的涂法,由分步乘法计数原理可知有5×4×4=80(种)不同的涂法.
由分类加法计数原理可得共有180+80=260(种)不同的涂法.
拓展衍生
1 2
3 4
课堂小结
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
归纳总结
利用分步乘法计数原理解题的一般思路
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
【课后作业】
教材 8页 A组1,2,3,4
教材 8页 B组1,2
