人教版数学七年级下册5.1.2 垂线 同步练习(含解析)
文档属性
| 名称 | 人教版数学七年级下册5.1.2 垂线 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 353.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-25 09:38:41 | ||
图片预览


文档简介
5.1.2 垂线 同步练习
一、单选题
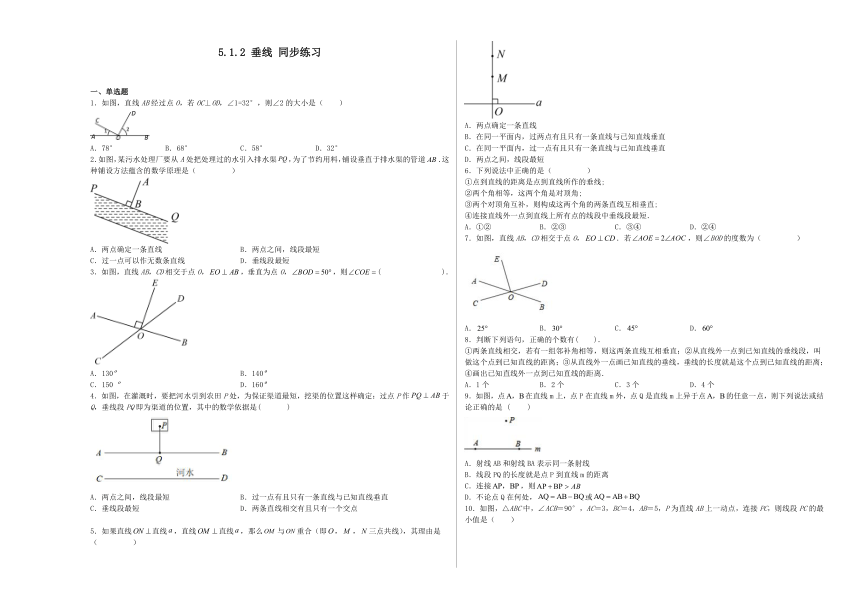
1.如图,直线AB经过点O,若OC⊥OD,∠1=32°,则∠2的大小是( )
A.78° B.68° C.58° D.32°
2.如图,某污水处理厂要从A处把处理过的水引入排水渠,为了节约用料,铺设垂直于排水渠的管道.这种铺设方法蕴含的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.过一点可以作无数条直线 D.垂线段最短
3.如图,直线AB,CD相交于点O,,垂直为点O,,则( ).
A.130 B.140
C.150 D.160
4.如图,在灌溉时,要把河水引到农田P处,为保证渠道最短,挖渠的位置这样确定:过点P作于Q,垂线段PQ即为渠道的位置,其中的数学依据是( )
A.两点之间,线段最短 B.过一点有且只有一条直线与已知直线垂直
C.垂线段最短 D.两条直线相交有且只有一个交点
5.如果直线直线,直线直线,那么与重合(即,,三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
6.下列说法中正确的是( )
①点到直线的距离是点到直线所作的垂线;
②两个角相等,这两个角是对顶角;
③两个对顶角互补,则构成这两个角的两条直线互相垂直;
④连接直线外一点到直线上所有点的线段中垂线段最短.
A.①② B.②③ C.③④ D.②④
7.如图,直线AB,CD相交于点O,.若,则∠BOD的度数为( )
A. B. C. D.
8.判断下列语句,正确的个数有( ).
①两条直线相交,若有一组邻补角相等,则这两条直线互相垂直;②从直线外一点到已知直线的垂线段,叫做这个点到已知直线的距离;③从直线外一点画已知直线的垂线,垂线的长度就是这个点到已知直线的距离;④画出已知直线外一点到已知直线的距离.
A.1个 B.2个 C.3个 D.4个
9.如图,点在直线m上,点P在直线m外,点Q是直线m上异于点的任意一点,则下列说法或结论正确的是 ( )
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接,则
D.不论点Q在何处,或
10.如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( )
A.3 B.2.5 C.2.4 D.2
二、填空题
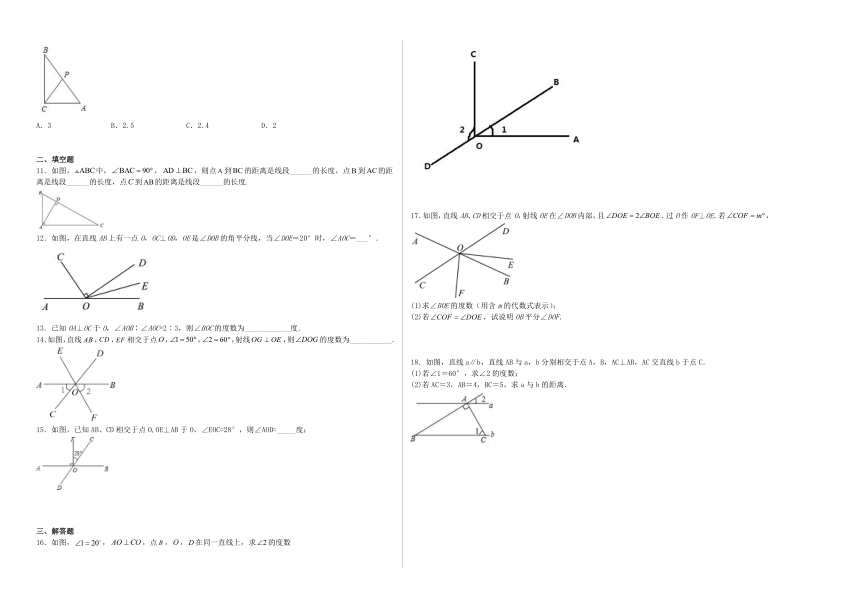
11.如图,中,,,则点到的距离是线段______的长度,点到的距离是线段______的长度,点到的距离是线段______的长度.
12.如图,在直线AB上有一点O,OC⊥OD,OE是∠DOB的角平分线,当∠DOE=20°时,∠AOC=___°.
13.已知OA⊥OC于O,∠AOB∶∠AOC=2∶3,则∠BOC的度数为____________度.
14.如图,直线,,相交于点,,,射线,则的度数为___________.
15.如图,已知AB、CD相交于点O,OE⊥AB于O,∠EOC=28°,则∠AOD=_____度;
三、解答题
16.如图,,,点,,在同一直线上,求的度数
17.如图,直线AB、CD相交于点O,射线OE在∠DOB内部,且.过O作OF⊥OE.若,
(1)求∠BOE的度数(用含m的代数式表示);
(2)若,试说明OB平分∠DOF.
18.如图,直线a∥b,直线AB与a,b分别相交于点A,B,AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求a与b的距离.
参考答案
1.C
【详解】
,
故选:C.
2.D
【详解】根据题意可知这种铺设方法蕴含的数学原理是垂线段最短.
故选D.
3.B
【详解】解:∵EO⊥AB,
∴
∵
∴
故选B.
4.C
【详解】解:∵PQ⊥AB,
∴PQ为农田P河水的距离最短,其中的数学道理是垂线段最短.
故选C.
5.C
【详解】解:如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),
其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
6.C
【详解】①应为点到直线的距离是这点到直线所做的垂线段的长度,故本小题错误;
②两个角相等,这两个角不一定是对顶角,故本小题错误;
③两个对顶角互补,则构成这两个角的两条直线互相垂直,正确;
④连接直线外一点到直线上所有点的线段中,中垂线段最短,正确;
所以正确的是③④.
故选C.
7.B
【详解】解: ,
,
故选B
8.A
【详解】解:由垂直的定义,知①正确;
从直线外一点到已知直线的垂线段的长度,叫做这个点到已知直线的距离,所以②、③、④都错误.
故选A.
9.C
【详解】解:A、射线AB和射线BA表示不同的射线,故A不符合题意;
B、PQ⊥AB时,线段PQ的长度就是点P到直线m的距离,故B不符合题意;
C、连接AP,BP,则AP+BP>AB,故C符合题意;
D、Q在A的右边时,AQ=AB-BQ或AQ=AB+BQ,故D不符合题意;
故选C.
10.C
【详解】解:在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴5PC=3×4,
∴PC=2.4,
故选:C.
11.
【详解】∵AD⊥BC,垂足为D,
∴点A到BC的距离是垂线段AD的长.
又∵∠BAC=90°,
∴CA⊥AB,
∴点到的距离是线段AB的长度,点到的距离是线段AC的长度.
故答案为AD,AB,AC.
12.
【详解】∵OE是∠DOB的角平分线,当∠DOE=20°
∴∠BOD=2∠DOE=40°
∵OC⊥OD,
∴∠AOC=180°-90°-∠BOD=50°
故答案为:50.
13.
【详解】解:∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=3:2,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.如图,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故答案为30°或150°.
14.
【详解】解:∵,,∠2=∠AOE,
∴∠EOD=180°-50°-60°=70°,
分两种情况:
①如图,
∵,
∴∠EOG=90°,
∴∠DOG=∠EOG-∠EOD=90°-70°=20°;
②如图,
∵∠EOG=90°,∠EOD=70°,
∴∠DOG=∠EOD+∠EOG=70°+90°=160°,
综上,的度数为20°或160°,
故答案为:20°或160°.
15.
【详解】解:∵,,
∴∠BOC=90°-28°=62°,
∵∠BOC=∠AOD,
∴∠AOD=62°.
故答案为:62.
16.
【详解】解:∵
∴
∵
∴
∵点,,在同一直线上,
∴.
17.
(1)
解:∵,
∴,
∵直线AB、CD相交于点O,
∴,
∵,
∴,
∵,
∴
(2)
解:∵且,
∴,
∵,
∴,
∴,,
∴.
∴OB平分.
18.
【详解】(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为a与b之间的距离.
∵AC⊥AB,
∴×AB×AC=×BC×AD,
∴AD==,
∴a与b的距离为.
一、单选题
1.如图,直线AB经过点O,若OC⊥OD,∠1=32°,则∠2的大小是( )
A.78° B.68° C.58° D.32°
2.如图,某污水处理厂要从A处把处理过的水引入排水渠,为了节约用料,铺设垂直于排水渠的管道.这种铺设方法蕴含的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.过一点可以作无数条直线 D.垂线段最短
3.如图,直线AB,CD相交于点O,,垂直为点O,,则( ).
A.130 B.140
C.150 D.160
4.如图,在灌溉时,要把河水引到农田P处,为保证渠道最短,挖渠的位置这样确定:过点P作于Q,垂线段PQ即为渠道的位置,其中的数学依据是( )
A.两点之间,线段最短 B.过一点有且只有一条直线与已知直线垂直
C.垂线段最短 D.两条直线相交有且只有一个交点
5.如果直线直线,直线直线,那么与重合(即,,三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
6.下列说法中正确的是( )
①点到直线的距离是点到直线所作的垂线;
②两个角相等,这两个角是对顶角;
③两个对顶角互补,则构成这两个角的两条直线互相垂直;
④连接直线外一点到直线上所有点的线段中垂线段最短.
A.①② B.②③ C.③④ D.②④
7.如图,直线AB,CD相交于点O,.若,则∠BOD的度数为( )
A. B. C. D.
8.判断下列语句,正确的个数有( ).
①两条直线相交,若有一组邻补角相等,则这两条直线互相垂直;②从直线外一点到已知直线的垂线段,叫做这个点到已知直线的距离;③从直线外一点画已知直线的垂线,垂线的长度就是这个点到已知直线的距离;④画出已知直线外一点到已知直线的距离.
A.1个 B.2个 C.3个 D.4个
9.如图,点在直线m上,点P在直线m外,点Q是直线m上异于点的任意一点,则下列说法或结论正确的是 ( )
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接,则
D.不论点Q在何处,或
10.如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( )
A.3 B.2.5 C.2.4 D.2
二、填空题
11.如图,中,,,则点到的距离是线段______的长度,点到的距离是线段______的长度,点到的距离是线段______的长度.
12.如图,在直线AB上有一点O,OC⊥OD,OE是∠DOB的角平分线,当∠DOE=20°时,∠AOC=___°.
13.已知OA⊥OC于O,∠AOB∶∠AOC=2∶3,则∠BOC的度数为____________度.
14.如图,直线,,相交于点,,,射线,则的度数为___________.
15.如图,已知AB、CD相交于点O,OE⊥AB于O,∠EOC=28°,则∠AOD=_____度;
三、解答题
16.如图,,,点,,在同一直线上,求的度数
17.如图,直线AB、CD相交于点O,射线OE在∠DOB内部,且.过O作OF⊥OE.若,
(1)求∠BOE的度数(用含m的代数式表示);
(2)若,试说明OB平分∠DOF.
18.如图,直线a∥b,直线AB与a,b分别相交于点A,B,AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求a与b的距离.
参考答案
1.C
【详解】
,
故选:C.
2.D
【详解】根据题意可知这种铺设方法蕴含的数学原理是垂线段最短.
故选D.
3.B
【详解】解:∵EO⊥AB,
∴
∵
∴
故选B.
4.C
【详解】解:∵PQ⊥AB,
∴PQ为农田P河水的距离最短,其中的数学道理是垂线段最短.
故选C.
5.C
【详解】解:如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),
其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
6.C
【详解】①应为点到直线的距离是这点到直线所做的垂线段的长度,故本小题错误;
②两个角相等,这两个角不一定是对顶角,故本小题错误;
③两个对顶角互补,则构成这两个角的两条直线互相垂直,正确;
④连接直线外一点到直线上所有点的线段中,中垂线段最短,正确;
所以正确的是③④.
故选C.
7.B
【详解】解: ,
,
故选B
8.A
【详解】解:由垂直的定义,知①正确;
从直线外一点到已知直线的垂线段的长度,叫做这个点到已知直线的距离,所以②、③、④都错误.
故选A.
9.C
【详解】解:A、射线AB和射线BA表示不同的射线,故A不符合题意;
B、PQ⊥AB时,线段PQ的长度就是点P到直线m的距离,故B不符合题意;
C、连接AP,BP,则AP+BP>AB,故C符合题意;
D、Q在A的右边时,AQ=AB-BQ或AQ=AB+BQ,故D不符合题意;
故选C.
10.C
【详解】解:在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴5PC=3×4,
∴PC=2.4,
故选:C.
11.
【详解】∵AD⊥BC,垂足为D,
∴点A到BC的距离是垂线段AD的长.
又∵∠BAC=90°,
∴CA⊥AB,
∴点到的距离是线段AB的长度,点到的距离是线段AC的长度.
故答案为AD,AB,AC.
12.
【详解】∵OE是∠DOB的角平分线,当∠DOE=20°
∴∠BOD=2∠DOE=40°
∵OC⊥OD,
∴∠AOC=180°-90°-∠BOD=50°
故答案为:50.
13.
【详解】解:∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=3:2,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.如图,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故答案为30°或150°.
14.
【详解】解:∵,,∠2=∠AOE,
∴∠EOD=180°-50°-60°=70°,
分两种情况:
①如图,
∵,
∴∠EOG=90°,
∴∠DOG=∠EOG-∠EOD=90°-70°=20°;
②如图,
∵∠EOG=90°,∠EOD=70°,
∴∠DOG=∠EOD+∠EOG=70°+90°=160°,
综上,的度数为20°或160°,
故答案为:20°或160°.
15.
【详解】解:∵,,
∴∠BOC=90°-28°=62°,
∵∠BOC=∠AOD,
∴∠AOD=62°.
故答案为:62.
16.
【详解】解:∵
∴
∵
∴
∵点,,在同一直线上,
∴.
17.
(1)
解:∵,
∴,
∵直线AB、CD相交于点O,
∴,
∵,
∴,
∵,
∴
(2)
解:∵且,
∴,
∵,
∴,
∴,,
∴.
∴OB平分.
18.
【详解】(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为a与b之间的距离.
∵AC⊥AB,
∴×AB×AC=×BC×AD,
∴AD==,
∴a与b的距离为.
