2.1.4多项式的乘法课后练习2022-2023学年湘教版七年级数学下册(无答案)
文档属性
| 名称 | 2.1.4多项式的乘法课后练习2022-2023学年湘教版七年级数学下册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 174.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-25 20:58:47 | ||
图片预览


文档简介
2.1.4多项式的乘法课后练习
一、单选题(共 8 小题)
1、8张如图1的长为,宽为()的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示,如果左上角与右下角的阴影部分的面积始终保持相等,则满足( )
A. B. C. D.
2、一个长方形的面积为,长为,则这个长方形的宽为( )
A. B. C. D.
3、小轩计算一道整式乘法的题:,由于小轩将第一个多项式中的“+2m”抄成“-2m”,得到的结果为.则m的值为( )
A.4 B.5 C.6 D.7
4、设(2x﹣1)3=ax3+bx2+cx+d,则下列结论:①a=8;②a+b+c+d=1;③a+c=14;④b+d=﹣13.正确的有( )
A.① B.①② C.①②③ D.①②③④
5、下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a6 C.(a3)2=a5 D.a3÷a2=a
6、下列各题中,计算正确的个数是( )
①(a-3b)(-6a)=-6a2+18ab;②(-x2y)(-9xy+2)=3x3y2+2;
③(-4ab)(-a2b)=2a3b2;④(-ab)(-ab2-2ab)=ab2-2ab.
A.1 B.2 C.3 D.4
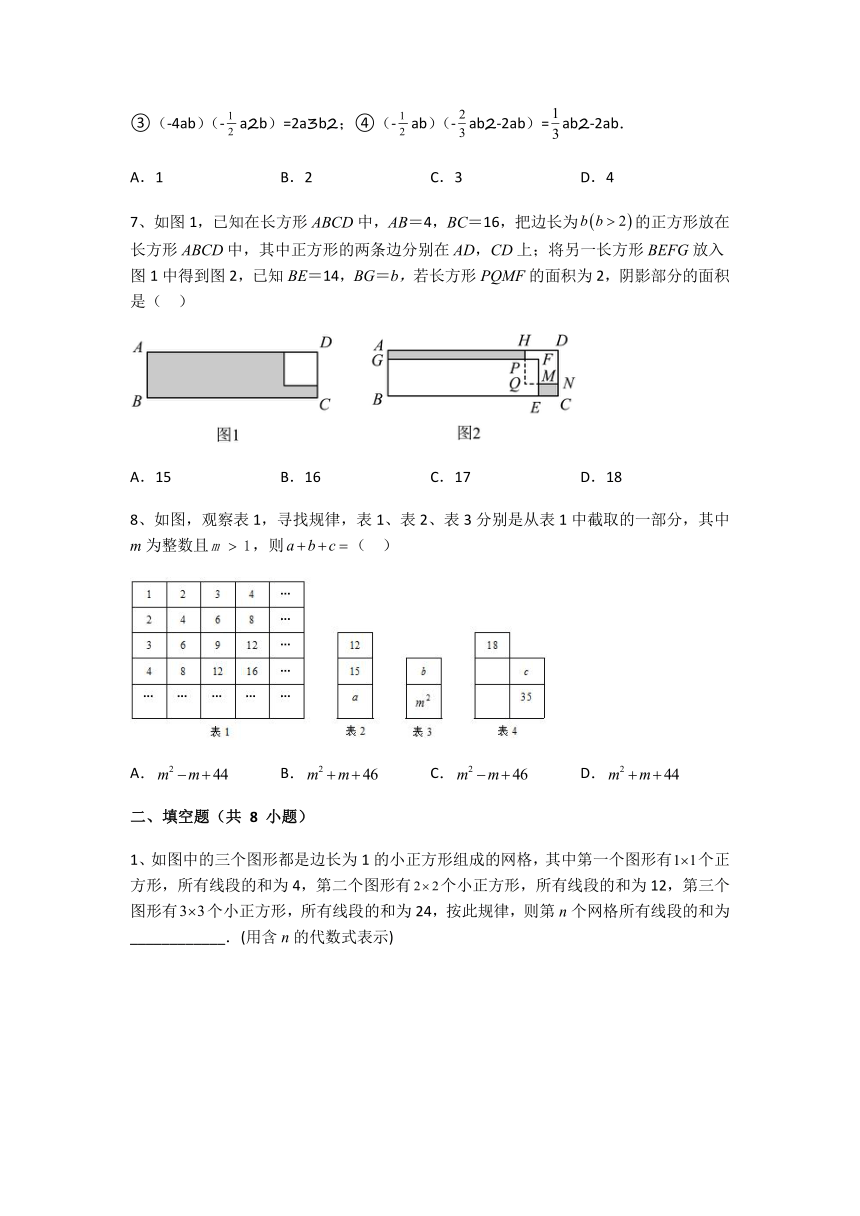
7、如图1,已知在长方形ABCD中,AB=4,BC=16,把边长为的正方形放在长方形ABCD中,其中正方形的两条边分别在AD,CD上;将另一长方形BEFG放入图1中得到图2,已知BE=14,BG=b,若长方形PQMF的面积为2,阴影部分的面积是( )
A.15 B.16 C.17 D.18
8、如图,观察表1,寻找规律,表1、表2、表3分别是从表1中截取的一部分,其中m为整数且,则( )
A. B. C. D.
二、填空题(共 8 小题)
1、如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有个正方形,所有线段的和为4,第二个图形有个小正方形,所有线段的和为12,第三个图形有个小正方形,所有线段的和为24,按此规律,则第n个网格所有线段的和为____________.(用含n的代数式表示)
2、若,则______.
3、若的积不含x的一次项和二次项,则a+b=______________.
4、已知的结果中不含项,则_____________.
5、若,,则___.
6、已知有因式,则_____.
7、已知,,则________.
8、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要___张C类卡片.
三、解答题(共 6 小题)
1、如图,某中学校园内有一块长为(3a+2b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块长为(2a﹣b)米、宽为2b米的小长方形地块修建一座雕像,然后将阴影部分进行绿化.
(1)求长方形地块的面积;(用含a,b的代数式表示)
(2)求修建雕像的小长方形地块的面积;(用含a,b的代数式表示)
(3)当a=3,b=1时,求绿化部分的面积.
2、已知:整式.
(1)化简整式;
(2)若,
①求整式;
②在“”的“□”内,填入“,,,”中的一个运算符号,经过计算发现,结果是不含一次项的整式,请你写出一个符合要求的算式,并计算出结果.
3、如图1,有一张长方形纸板,在它的四角各切去一个大小相同的正方形,然后将四周突出部分折起,制成一个高为a厘米的长方体形状的无盖纸盒(如图2).如果纸盒的体积为(2a2b+ab2)立方厘米,底面长方形的宽为b厘米.
(1)求这张长方形纸板的长;
(2)将长方体形状的无盖纸盒的外表面都贴一层红色的包装纸,请求出一个这样的纸盒需要用多少平方厘米的红色包装纸.(结果都用含a,b的代数式表示)
4、若的展开式中不含和项,求:
(1) 的值.
(2)求的值.
5、计算:
(1)
(2)
6、先化简,再求值.
(1)[(2x+y)(2x﹣y)﹣(2x﹣3y)2]÷(2y),其中x=2,y=1;
(2)(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
一、单选题(共 8 小题)
1、8张如图1的长为,宽为()的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示,如果左上角与右下角的阴影部分的面积始终保持相等,则满足( )
A. B. C. D.
2、一个长方形的面积为,长为,则这个长方形的宽为( )
A. B. C. D.
3、小轩计算一道整式乘法的题:,由于小轩将第一个多项式中的“+2m”抄成“-2m”,得到的结果为.则m的值为( )
A.4 B.5 C.6 D.7
4、设(2x﹣1)3=ax3+bx2+cx+d,则下列结论:①a=8;②a+b+c+d=1;③a+c=14;④b+d=﹣13.正确的有( )
A.① B.①② C.①②③ D.①②③④
5、下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a6 C.(a3)2=a5 D.a3÷a2=a
6、下列各题中,计算正确的个数是( )
①(a-3b)(-6a)=-6a2+18ab;②(-x2y)(-9xy+2)=3x3y2+2;
③(-4ab)(-a2b)=2a3b2;④(-ab)(-ab2-2ab)=ab2-2ab.
A.1 B.2 C.3 D.4
7、如图1,已知在长方形ABCD中,AB=4,BC=16,把边长为的正方形放在长方形ABCD中,其中正方形的两条边分别在AD,CD上;将另一长方形BEFG放入图1中得到图2,已知BE=14,BG=b,若长方形PQMF的面积为2,阴影部分的面积是( )
A.15 B.16 C.17 D.18
8、如图,观察表1,寻找规律,表1、表2、表3分别是从表1中截取的一部分,其中m为整数且,则( )
A. B. C. D.
二、填空题(共 8 小题)
1、如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有个正方形,所有线段的和为4,第二个图形有个小正方形,所有线段的和为12,第三个图形有个小正方形,所有线段的和为24,按此规律,则第n个网格所有线段的和为____________.(用含n的代数式表示)
2、若,则______.
3、若的积不含x的一次项和二次项,则a+b=______________.
4、已知的结果中不含项,则_____________.
5、若,,则___.
6、已知有因式,则_____.
7、已知,,则________.
8、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要___张C类卡片.
三、解答题(共 6 小题)
1、如图,某中学校园内有一块长为(3a+2b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块长为(2a﹣b)米、宽为2b米的小长方形地块修建一座雕像,然后将阴影部分进行绿化.
(1)求长方形地块的面积;(用含a,b的代数式表示)
(2)求修建雕像的小长方形地块的面积;(用含a,b的代数式表示)
(3)当a=3,b=1时,求绿化部分的面积.
2、已知:整式.
(1)化简整式;
(2)若,
①求整式;
②在“”的“□”内,填入“,,,”中的一个运算符号,经过计算发现,结果是不含一次项的整式,请你写出一个符合要求的算式,并计算出结果.
3、如图1,有一张长方形纸板,在它的四角各切去一个大小相同的正方形,然后将四周突出部分折起,制成一个高为a厘米的长方体形状的无盖纸盒(如图2).如果纸盒的体积为(2a2b+ab2)立方厘米,底面长方形的宽为b厘米.
(1)求这张长方形纸板的长;
(2)将长方体形状的无盖纸盒的外表面都贴一层红色的包装纸,请求出一个这样的纸盒需要用多少平方厘米的红色包装纸.(结果都用含a,b的代数式表示)
4、若的展开式中不含和项,求:
(1) 的值.
(2)求的值.
5、计算:
(1)
(2)
6、先化简,再求值.
(1)[(2x+y)(2x﹣y)﹣(2x﹣3y)2]÷(2y),其中x=2,y=1;
(2)(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
