18.1.2 平行四边形的判定 考点专项练- 2022-2023学年初中数学人教版八年级下册(含答案))
文档属性
| 名称 | 18.1.2 平行四边形的判定 考点专项练- 2022-2023学年初中数学人教版八年级下册(含答案)) |
|
|
| 格式 | docx | ||
| 文件大小 | 536.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-25 21:47:09 | ||
图片预览

文档简介
18.1.2 平行四边形的判定
1.在Rt△ABC中,∠B=90°,D,E,F分别是边BC,CA,AB的中点,AB=6,BC=8,则四边形AEDF的周长是( )
A.18 B.16 C.14 D.12
2.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
3.如图,点D,E分别是△ABC边BA,BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
4.中,点D、E、F分别为边的中点,作.若的面积是12,则的面积是( )
A.2 B.3 C.4 D.6
5.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=84°,则∠FEG等于( )
A.32° B.38° C.64° D.30°
6.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5 B.5 C.5.5 D.6
7.△ABC的面积为4cm2,D、E、F分别是AE,BC,CD的中点,则△BDF的面积为( )
A.2 cm2, B.1 cm2,
C.0.5 cm2, D.0.25 cm2,
8.在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )
A.9.5 B.10.5 C.11 D.15.5
9.如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为( ).
A.8 m B.4 m C.2 m D.6 m
10.如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
A.300 B.315 C.279 D.342
11.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为 ( )
A.cm B.4cm C.cm D.cm
12.△ABC中,D、E、F分别为AB、AC、BC的中点, 若△DEF的周长为6,则△ABC周长为( ).
A.3 B.6 C.12 D.24
13.如图,在中,若,,则下列线段是的中位线的是( )
A. B. C. D.
14.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
15.如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A.2 B.4 C.8 D.10
16.如图,在平行四边形中,对角线与相交于点,是边的中点,连接,若,,则的度数为( )
A. B. C. D.
17..如图,矩形中,是的中点,点 在 边上运动,, 分别是 , 的中点,则的长随着点的运动( )
A.变短 B.变长 C.不变 D.无法确定
18.如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
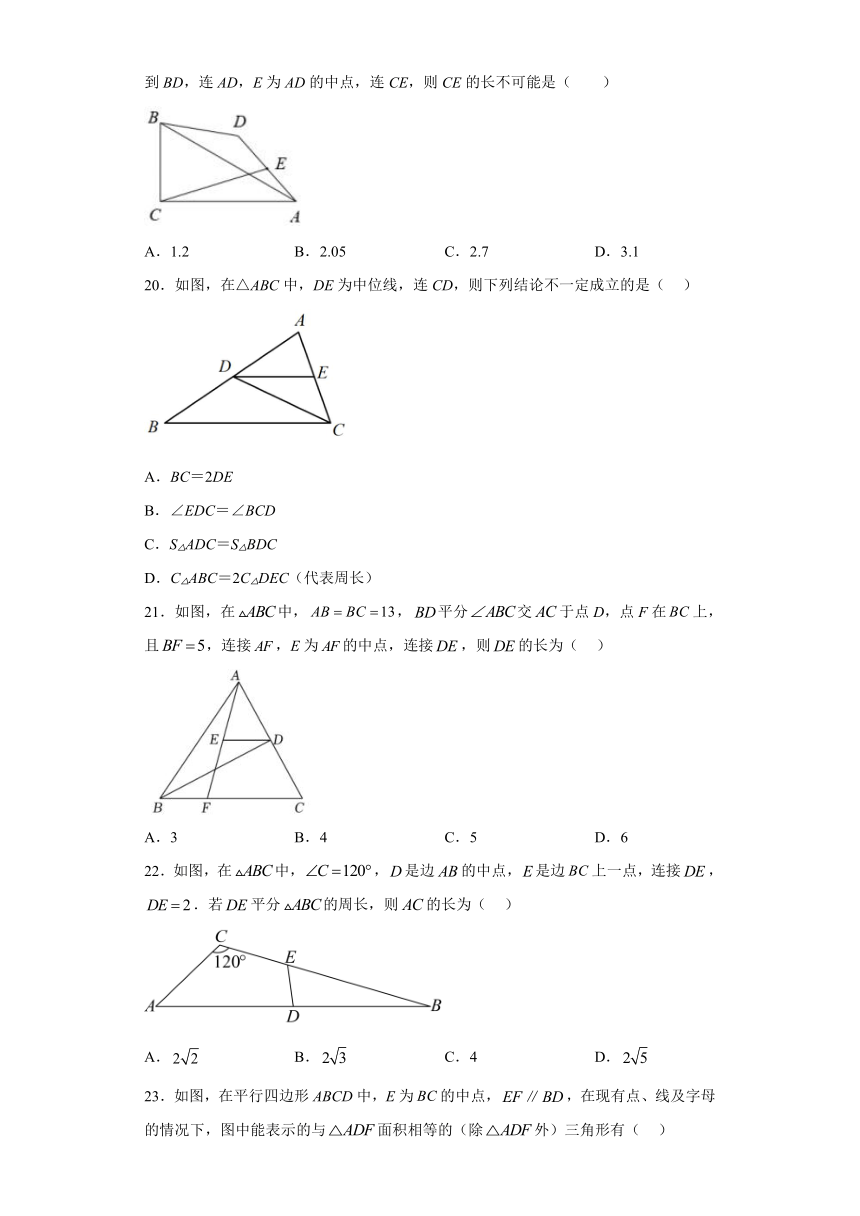
19.如图,在RtABC中,∠ACB=90°,∠BAC=30°,BC=2,线段BC绕点B旋转到BD,连AD,E为AD的中点,连CE,则CE的长不可能是( )
A.1.2 B.2.05 C.2.7 D.3.1
20.如图,在△ABC中,DE为中位线,连CD,则下列结论不一定成立的是( )
A.BC=2DE
B.∠EDC=∠BCD
C.S△ADC=S△BDC
D.C△ABC=2C△DEC(代表周长)
21.如图,在中,,平分交于点D,点F在上,且,连接,E为的中点,连接,则的长为( )
A.3 B.4 C.5 D.6
22.如图,在中,,是边的中点,是边上一点,连接,.若平分的周长,则的长为( )
A. B. C.4 D.
23.如图,在平行四边形ABCD中,E为的中点,,在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A.3个 B.4个 C.5个 D.6个
24.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为( )
A.32 B.16 C.8 D.4
25.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
参考答案:
1.B
2.C
试题分析:由题意得,∠AED=180°﹣∠A﹣∠ADE=70°,
∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线.
∴DE∥BC.∴∠C=∠AED=70°.
3.D
4.B
解:过A作AH⊥BC于H,取BH中点为G,连结DG,EM⊥DF于M,
∵、分别是的、边的中点,
∴,DF∥BC,
∵D、G为AB、BH中点,
∴DG∥AH,且DG=,
∵AH⊥BC
∴DG⊥BC,
∵DF∥BC,EM⊥DF
∴DG⊥DF,
∴DG=ME=
∵S△ABC=
∴.
故选择B.
5.A
解:∵AD=BC,E,F,G分别是AB,CD,AC的中点,
∴GF是△ACD的中位线,GE是△ACB的中位线,
∴GF=AD,GF∥AD,GE=BC,GE∥BC.
又∵AD=BC,
∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=84°,
∴∠EFG=∠FEG,
∵∠FGE=∠FGC+∠EGC=20°+(180°-84°)=116°,
∴∠EFG=(180°-∠FGE)=32°.
6.A
∵点D,E,F,G分别是BC,AD,BE,CE的中点,
∴AD是△ABC的中线,BE是△ABD的中线,CE是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,
∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,
同理可得△AEG的面积=,
△BCE的面积=×△ABC的面积=6,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积=,
∴△AFG的面积=△AEF的面积+△AEG的面积+△EFG的面积=×3=4.5,
7.B
∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD= S△ABC= ×4=2,
同理S△BDE=S△CDE= S△BCE= ×2=1,
∴S△BCE=2,
∵F为EC中点,
∴S△BEF= S△BCE=×2=1.
8.D
解:∵△EDF是△EAF折叠以后形成的图形,
∴△EDF≌△EAF,AD⊥EF,
∴∠AEF=∠DEF,
∵AD是BC边上的高,
∴EF∥CB,
又∵∠AEF=∠B,
∴∠BDE=∠DEF,
∴∠B=∠BDE,
∴BE=DE,
同理,DF=CF,
∴EF为△ABC的中位线,
∴△DEF的周长为△EAF的周长,
即AE+EF+AF=(AB+BC+AC)=(12+10+9)=15.5.
9.B
解:∵∠A=30°,AB=16m,∠ACB=90°,
∴BC=AB=×16=8m,
∵BC、DE垂直于横梁AC,
∴BC//DE,
∵点D是斜梁AB的中点,
∴AE=CE
∴DE=BC=×8=4m.
10.B
解:设△BPE的面积为x,△APE的面积为y,
由等高不等底的三角形的面积的比等于底边的比,得:,①
②
两式联立解得:x=56,y=70,
∴△ABC的面积=84+70+35+40+30+56=315.
11.D
解:∵点D、E分别是边AB、AC的中点,
∴DE=BC,
∵DE=2cm,
∴BC=4cm,
∵AB=AC,四边形DEFG是正方形.
∴∠B=∠C,DG=EF=2,∠DGF=∠EFG=90°,
∴∠DGB=∠EFC=90°,
∴△BDG≌△CEF,
∴BG=CF=1,
∴EC=,
∴AC=2cm.
12.C
13.A
14.C
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
15.C
16.D
解:,,
,
四边形是平行四边形,对角线与相交于点O,
,
E是边的中点,
∴,
17.C
18.B
解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
19.D
解:取AB的中点F,连接EF、CF,
∵∠BAC=30°,BC=2,
∴AB=2BC=4,BF=FA=BC=CF=2,∠ABC=60°,
∴△BCF是等边三角形,
∵E、F分别是AD、AB的中点,
∴EF=BD=1,
如图:
当C、E、F共线时CE有最大值,最大值为CF+EF=3;
如图,
当C、E、F共线时CE有最小值,最小值为CF-EF=1;
∴,
观察各选项,只有选项D符合题意,
20.D
解:∵在△ABC中,DE为中位线,
∴DE∥BC,DE=,
∴BC=2DE,
∴选项A正确,不符合题意;
∵DE∥BC,
∴∠EDC=∠BCD,
故选项B正确,不符合题意;
∵DE为△ABC的中位线,
∴D为AB中点,
∴AD=BD,
过C作CH⊥AB于H,
∴CH是△BCD的高,也是△ACD的高,
∴S△ADC=,
S△BDC=,
∴S△ADC= S△BDC,
故选项C正确,不符合题意;
∵CD为AB边中线,
当∠ACB=90°时,
∴AB=2CD,
∵BC=2DE,点E为AC中点,
∴AC=2EC,
∵C△ABC=AB+BC+CA=2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC= 2C△DEC,
当∠ACB≠90°时,
AB≠2CD,
∴C△ABC=AB+BC+CA≠2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC≠2C△DEC,
∴选项D的结论不一定成立,符合题意.
21.B
解:由题意可得:,
∵,平分,
∴为中线,即为的中点,
又∵E为的中点,
∴为的中位线,
∴,
22.C
解:如图,延长至,使得,连接,
,
,
又,
是等边三角形,
,
是边的中点,是边上一点,平分的周长,
,,
,
,
,
即,
是的中位线,,
.
23.C
E为的中点,,
F为中点,
四边形ABCD为平行四边形,
,,
是的中线,是的中线,是的中线,
,
能表示的与面积相等的(除外)三角形有5个,
故选:C.
24.C
∵AD=AC,
∴是等腰三角形,
∵AE⊥CD,
∴,
∴E是CD的中点,
∵F是BC的中点,
∴EF是△BCD的中位线,
∴,
25.B
解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
1.在Rt△ABC中,∠B=90°,D,E,F分别是边BC,CA,AB的中点,AB=6,BC=8,则四边形AEDF的周长是( )
A.18 B.16 C.14 D.12
2.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
3.如图,点D,E分别是△ABC边BA,BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
4.中,点D、E、F分别为边的中点,作.若的面积是12,则的面积是( )
A.2 B.3 C.4 D.6
5.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=84°,则∠FEG等于( )
A.32° B.38° C.64° D.30°
6.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A.4.5 B.5 C.5.5 D.6
7.△ABC的面积为4cm2,D、E、F分别是AE,BC,CD的中点,则△BDF的面积为( )
A.2 cm2, B.1 cm2,
C.0.5 cm2, D.0.25 cm2,
8.在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )
A.9.5 B.10.5 C.11 D.15.5
9.如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=16m,则DE的长为( ).
A.8 m B.4 m C.2 m D.6 m
10.如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
A.300 B.315 C.279 D.342
11.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为 ( )
A.cm B.4cm C.cm D.cm
12.△ABC中,D、E、F分别为AB、AC、BC的中点, 若△DEF的周长为6,则△ABC周长为( ).
A.3 B.6 C.12 D.24
13.如图,在中,若,,则下列线段是的中位线的是( )
A. B. C. D.
14.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
15.如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A.2 B.4 C.8 D.10
16.如图,在平行四边形中,对角线与相交于点,是边的中点,连接,若,,则的度数为( )
A. B. C. D.
17..如图,矩形中,是的中点,点 在 边上运动,, 分别是 , 的中点,则的长随着点的运动( )
A.变短 B.变长 C.不变 D.无法确定
18.如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
19.如图,在RtABC中,∠ACB=90°,∠BAC=30°,BC=2,线段BC绕点B旋转到BD,连AD,E为AD的中点,连CE,则CE的长不可能是( )
A.1.2 B.2.05 C.2.7 D.3.1
20.如图,在△ABC中,DE为中位线,连CD,则下列结论不一定成立的是( )
A.BC=2DE
B.∠EDC=∠BCD
C.S△ADC=S△BDC
D.C△ABC=2C△DEC(代表周长)
21.如图,在中,,平分交于点D,点F在上,且,连接,E为的中点,连接,则的长为( )
A.3 B.4 C.5 D.6
22.如图,在中,,是边的中点,是边上一点,连接,.若平分的周长,则的长为( )
A. B. C.4 D.
23.如图,在平行四边形ABCD中,E为的中点,,在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A.3个 B.4个 C.5个 D.6个
24.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为( )
A.32 B.16 C.8 D.4
25.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
参考答案:
1.B
2.C
试题分析:由题意得,∠AED=180°﹣∠A﹣∠ADE=70°,
∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线.
∴DE∥BC.∴∠C=∠AED=70°.
3.D
4.B
解:过A作AH⊥BC于H,取BH中点为G,连结DG,EM⊥DF于M,
∵、分别是的、边的中点,
∴,DF∥BC,
∵D、G为AB、BH中点,
∴DG∥AH,且DG=,
∵AH⊥BC
∴DG⊥BC,
∵DF∥BC,EM⊥DF
∴DG⊥DF,
∴DG=ME=
∵S△ABC=
∴.
故选择B.
5.A
解:∵AD=BC,E,F,G分别是AB,CD,AC的中点,
∴GF是△ACD的中位线,GE是△ACB的中位线,
∴GF=AD,GF∥AD,GE=BC,GE∥BC.
又∵AD=BC,
∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=84°,
∴∠EFG=∠FEG,
∵∠FGE=∠FGC+∠EGC=20°+(180°-84°)=116°,
∴∠EFG=(180°-∠FGE)=32°.
6.A
∵点D,E,F,G分别是BC,AD,BE,CE的中点,
∴AD是△ABC的中线,BE是△ABD的中线,CE是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,
∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,
同理可得△AEG的面积=,
△BCE的面积=×△ABC的面积=6,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积=,
∴△AFG的面积=△AEF的面积+△AEG的面积+△EFG的面积=×3=4.5,
7.B
∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD= S△ABC= ×4=2,
同理S△BDE=S△CDE= S△BCE= ×2=1,
∴S△BCE=2,
∵F为EC中点,
∴S△BEF= S△BCE=×2=1.
8.D
解:∵△EDF是△EAF折叠以后形成的图形,
∴△EDF≌△EAF,AD⊥EF,
∴∠AEF=∠DEF,
∵AD是BC边上的高,
∴EF∥CB,
又∵∠AEF=∠B,
∴∠BDE=∠DEF,
∴∠B=∠BDE,
∴BE=DE,
同理,DF=CF,
∴EF为△ABC的中位线,
∴△DEF的周长为△EAF的周长,
即AE+EF+AF=(AB+BC+AC)=(12+10+9)=15.5.
9.B
解:∵∠A=30°,AB=16m,∠ACB=90°,
∴BC=AB=×16=8m,
∵BC、DE垂直于横梁AC,
∴BC//DE,
∵点D是斜梁AB的中点,
∴AE=CE
∴DE=BC=×8=4m.
10.B
解:设△BPE的面积为x,△APE的面积为y,
由等高不等底的三角形的面积的比等于底边的比,得:,①
②
两式联立解得:x=56,y=70,
∴△ABC的面积=84+70+35+40+30+56=315.
11.D
解:∵点D、E分别是边AB、AC的中点,
∴DE=BC,
∵DE=2cm,
∴BC=4cm,
∵AB=AC,四边形DEFG是正方形.
∴∠B=∠C,DG=EF=2,∠DGF=∠EFG=90°,
∴∠DGB=∠EFC=90°,
∴△BDG≌△CEF,
∴BG=CF=1,
∴EC=,
∴AC=2cm.
12.C
13.A
14.C
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
15.C
16.D
解:,,
,
四边形是平行四边形,对角线与相交于点O,
,
E是边的中点,
∴,
17.C
18.B
解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
19.D
解:取AB的中点F,连接EF、CF,
∵∠BAC=30°,BC=2,
∴AB=2BC=4,BF=FA=BC=CF=2,∠ABC=60°,
∴△BCF是等边三角形,
∵E、F分别是AD、AB的中点,
∴EF=BD=1,
如图:
当C、E、F共线时CE有最大值,最大值为CF+EF=3;
如图,
当C、E、F共线时CE有最小值,最小值为CF-EF=1;
∴,
观察各选项,只有选项D符合题意,
20.D
解:∵在△ABC中,DE为中位线,
∴DE∥BC,DE=,
∴BC=2DE,
∴选项A正确,不符合题意;
∵DE∥BC,
∴∠EDC=∠BCD,
故选项B正确,不符合题意;
∵DE为△ABC的中位线,
∴D为AB中点,
∴AD=BD,
过C作CH⊥AB于H,
∴CH是△BCD的高,也是△ACD的高,
∴S△ADC=,
S△BDC=,
∴S△ADC= S△BDC,
故选项C正确,不符合题意;
∵CD为AB边中线,
当∠ACB=90°时,
∴AB=2CD,
∵BC=2DE,点E为AC中点,
∴AC=2EC,
∵C△ABC=AB+BC+CA=2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC= 2C△DEC,
当∠ACB≠90°时,
AB≠2CD,
∴C△ABC=AB+BC+CA≠2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC≠2C△DEC,
∴选项D的结论不一定成立,符合题意.
21.B
解:由题意可得:,
∵,平分,
∴为中线,即为的中点,
又∵E为的中点,
∴为的中位线,
∴,
22.C
解:如图,延长至,使得,连接,
,
,
又,
是等边三角形,
,
是边的中点,是边上一点,平分的周长,
,,
,
,
,
即,
是的中位线,,
.
23.C
E为的中点,,
F为中点,
四边形ABCD为平行四边形,
,,
是的中线,是的中线,是的中线,
,
能表示的与面积相等的(除外)三角形有5个,
故选:C.
24.C
∵AD=AC,
∴是等腰三角形,
∵AE⊥CD,
∴,
∴E是CD的中点,
∵F是BC的中点,
∴EF是△BCD的中位线,
∴,
25.B
解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
