人教版数学七年级下册7.2坐标方法的简单应用(含解析)
文档属性
| 名称 | 人教版数学七年级下册7.2坐标方法的简单应用(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 13:48:53 | ||
图片预览



文档简介
7.2 坐标方法的简单应用
一、单选题
1.在直角坐标系中,将点(-2, -3)向左平移2个单位长度得到的点的坐标是( )
A.(-2,-5) B.(-4,-3) C.(0,-3) D.(-2,1)
2.下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为轴、轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为,表示水宁阁的点的坐标为,那么下列各场馆的坐标表示正确的是( )
A.中国馆的坐标为
B.国际馆的坐标为
C.生活体验馆的坐标为
D.植物馆的坐标为
3.如图表示点A的位置,正确的是( )
A.距离O点3km的地方
B.在O点北偏东40°方向,距O点3km的地方
C.在O点东偏北40°的方向上
D.在O点北偏东50°方向,距O点3m的地方
4.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于y轴对称
5.在平面直角坐标系中,点A的坐标是(–1,2),作点A关于y轴的对称点,得到点A',再将点A'向下平移4个单位,得到点A″,则点A″的坐标是( )
A.(–1,–2) B.(1,2) C.(1,–2) D.(–2,1)
6.如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=( )
A.0 B.﹣49 C.50 D.﹣50
7.把点A(-2,1)向上平移2个单位,再向右平移3个单位后得到B,点B的坐标是( ).
A.(-5,3) B.(1,3) C.(1,-3) D.(-5,-1)
8.线段MN是由线段EF经过平移得到的,若点E(-1,3)的对应点M(2,1),则点F (-3,-2)的对应点N的坐标是( )
A.(-1,0) B.(-6,0) C.(0,-4) D.(0,0)
9.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
10.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
二、填空题
11.如果将点A(-3,-1)向右平移2个单位长度,再向下平移3个单位得到点B,那么点B的坐标是________.
12.将点向左平移个单位长度后可得到对应点坐标是________;将点向上平移单位长度后可得对应点坐标是________.
13.一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作_________平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的_________;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
14.在平面直角坐标系中,把点A(2,3)向左平移一个单位得到点A′,则点A′的坐标为_____.
15.在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
(1)当a=1时,则点Q的坐标为____;
(2)当点P在直线上运动时,点Q也随之运动.当a=___时,AQ+BQ的值最小为____.
三、解答题
16.在学习完《位置与坐标》,小斌、小亮、小敏和小芳设计了一个游戏,他们在操场上画了如图所示,每小格边长均为的方格.若小斌从点出发,依次到点(小亮),(小敏),(小芳)处,规定:向北和向东走为正,向南和向西走为负如果从到记为,从到记为,数对中的第一个数表示东西方向,第二个数表示南北方向.
(1)图中的到,到分别记为______;
(2)若小斌的行走路线为,请计算小斌走过的路程;
(3)若小亮从点出发到点,行走的路线依次为,,请在图中标出点的位置;
(4)若图中有两个格点,,且点,,则应记为______.
17.如图所示,已知点A(2,1),B(8,2),C(6,3).
(1)若将△ABC向下平移 5个单位长度,再向左平移 9个单位长度,得到△ ′ ′ ′,画出平移后图形并写出各顶点的坐标.
(2)求△ABC的面积.
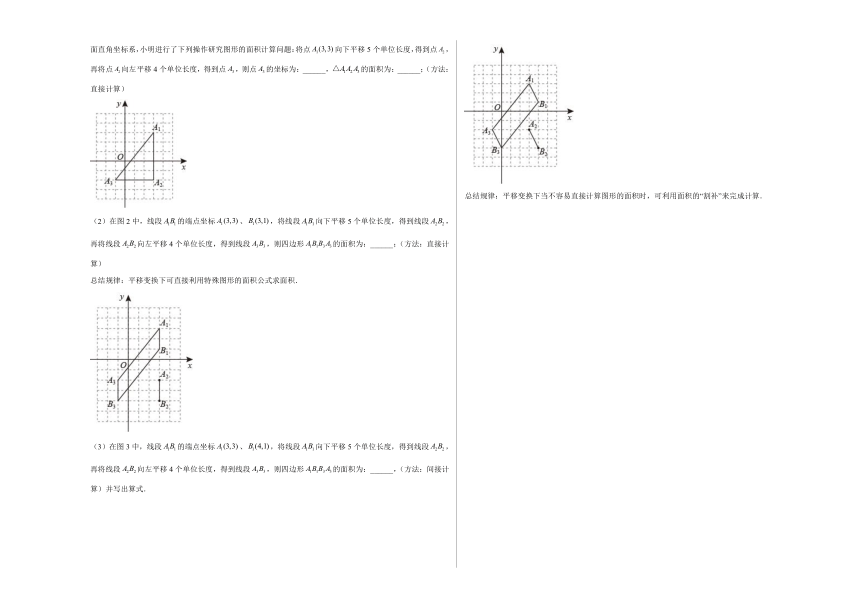
18.综合与实践(1)动手、计算:数学活动课上,在边长为1的小正方形组成的网格中建立如图1所示的平面直角坐标系,小明进行了下列操作研究图形的面积计算问题:将点向下平移5个单位长度,得到点,再将点向左平移4个单位长度,得到点,则点的坐标为:______,的面积为:______;(方法:直接计算)
(2)在图2中,线段的端点坐标、,将线段向下平移5个单位长度,得到线段,再将线段向左平移4个单位长度,得到线段,则四边形的面积为:______;(方法:直接计算)
总结规律:平移变换下可直接利用特殊图形的面积公式求面积.
(3)在图3中,线段的端点坐标、,将线段向下平移5个单位长度,得到线段,再将线段向左平移4个单位长度,得到线段,则四边形的面积为:______,(方法:间接计算)并写出算式.
总结规律:平移变换下当不容易直接计算图形的面积时,可利用面积的“割补”来完成计算.
参考答案
1.B
【详解】( 2, 3)向左平移2个单位长度得到的点的坐标是:( 4, 3).
故选B.
2.A
【详解】解:根据题意可建立如下所示平面直角坐标系,
A、中国馆的坐标为(-1,-2),故本选项正确;
B、国际馆的坐标为(3,-1),故本选项错误;
C、生活体验馆的坐标为(7,4),故本选项错误;
D、植物馆的坐标为(-7,-4),故本选项错误.
故选A.
3.D
【详解】由图可得,点A在O点北偏东50°方向,距O点3m的地方,
故选D.
4.A
【详解】解:∵将三角形三个顶点的横坐标都减2,纵坐标不变,
∴所得三角形与原三角形的关系是:将原图向左平移两个单位.
故选:A.
5.C
【详解】∵点A的坐标是(﹣1,2),作点A关于y轴的对称点,得到点A'
∴A′(1,2)
∵将点A'向下平移4个单位,得到点A″
∴点A″的坐标是:(1,﹣2)
故选C
6.C
经过观察分析可得每4个数的和为2,把100个数分为25组,即可得到相应结果.
详解:x1+x2+x3+x4=1-1-1+3=2;
x5+x6+x7+x8=3-3-3+5=2;
…
x97+x98+x99+x100=2;
∴原式=2×(100÷4)=50.
故选C.
7.B
∵A(-2,1)向上平移2个单位,再向右平移3个单位后得到B
∴1+2=3,-2+3=1
点B的坐标是(1,3)
故选B.
8.C
【详解】解:点E(-1,3)向右平移3个单位长度,向下移2个单位长度到M(2,1),所以点F(-3,-2)也向右平移3个单位长度,向下平移2个单位长度,得到点N(0,-4).
故选C.
9.B
【详解】跳蚤运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依次类推,到(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).
故选B.
10.B
【详解】由题意知(10,20)表示向东走10米,再向北走20米,故为B点.
故选:B.
11.解:将点A(-3,-1)向右平移2个单位长度再向下平移3个单位长度得到点B(-3+2,-1-3)
即(-1,-4),
故答案为:(-1,-4).
12. 解:(2,﹣5)向左平移3个单位长度后可得到对应点坐标是(﹣5,﹣5);
将点(2,+5)向上平移3单位长度后可得对应点坐标是(2,8).
故答案为(﹣5,﹣5)和(2,8).
13. 一次 变化
14.解:∵点A(2,3)向左平移1个单位长度,
∴点A′的横坐标为2-1=1,纵坐标不变,
∴A′的坐标为(1,3).
故答案为:(1,3).
15. (1)过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,如图1.∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°.∵∠APQ=90°,∴∠EPA=∠FPQ=90°﹣∠APF.在△PEA和△PFQ中,,∴△PEA≌△PFQ.∴PE=PF,EA=QF.∵a=1,∴P(1,3).∴OE=BP=1,PE=3.∵A(2,0),∴OA=2,∴EA=1.∴PF=3,QF=1.∴点Q的坐标为(4,4).
(2)若点P的坐标为(a,3),则PF=PE=3,QF=AE=|2﹣a|.∴点Q的坐标为(a+3,5﹣a).∵无论a为何值,点Q的坐标(a+3,5﹣a)都满足一次函数解析式y=﹣x+8,∴点Q始终在直线y=﹣x+8上运动.设直线y=﹣x+8与x轴、y轴分别交于点M、N,如图2所示.当x=0时y=8,当y=0时x=8.∴OM=ON=8.∵∠AOB=90°,∴∠OMN=45°.过点A关于直线MN作对称点A′,连A′Q、A′M,则A′Q=AQ,A′M=AM=6,∠A′MN=∠AMN=45°.∴∠A′MA=90°,AQ+BQ=A′Q+BQ.根据两点之间线段最短可知:当A′、Q、B三点共线时,AQ+BQ=A′Q+BQ最短,最小值为A′B长.设直线BP与A′M相交于点H,则BH⊥A′M.在Rt△A′HB中,∠A′HB=90,BH=OM=8,A′H=A′M﹣MH=6﹣3=3,∴A′B= ==.当A′、Q、B三点共线时,∵BN∥A′M,∴△BQN~△A′QM.根据相似三角形对应高的比等于相似比可得:,解得xQ=.∴a+3=.∴a=.∴当a=时,AQ+BQ的值最小为.
故答案为(1)(4,4);(2);.
16.(1)由题意,得,;
(2)
,
.
所以,小斌走过了.
(3)如图所示:
(4)∵点,,
∴为
即.
17.解:(1)根据题意,如图即为所求,
A’(-7,-4) ,B’(-1,-3) ,C’(-3,-2)
(2)S△ABC=62---=12-4-1-3=4
18.解:(1)由题意可得:A1(3,3)、A2(3,-2)、A3(-1,-2),
∴A1A2=5,A2A3=4,∠A1A2A3=90°,
∴△A1A2A3的面积=×4×5=10;
故填(-1,-2),10;
(2)由题意得:A1B1=3-1=2
∴四边形A1B1B3A3的面积为=2×4=8;
故填8;
(3)四边形A1B1B3A3的面积=.
故填13.
一、单选题
1.在直角坐标系中,将点(-2, -3)向左平移2个单位长度得到的点的坐标是( )
A.(-2,-5) B.(-4,-3) C.(0,-3) D.(-2,1)
2.下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为轴、轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为,表示水宁阁的点的坐标为,那么下列各场馆的坐标表示正确的是( )
A.中国馆的坐标为
B.国际馆的坐标为
C.生活体验馆的坐标为
D.植物馆的坐标为
3.如图表示点A的位置,正确的是( )
A.距离O点3km的地方
B.在O点北偏东40°方向,距O点3km的地方
C.在O点东偏北40°的方向上
D.在O点北偏东50°方向,距O点3m的地方
4.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于y轴对称
5.在平面直角坐标系中,点A的坐标是(–1,2),作点A关于y轴的对称点,得到点A',再将点A'向下平移4个单位,得到点A″,则点A″的坐标是( )
A.(–1,–2) B.(1,2) C.(1,–2) D.(–2,1)
6.如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=( )
A.0 B.﹣49 C.50 D.﹣50
7.把点A(-2,1)向上平移2个单位,再向右平移3个单位后得到B,点B的坐标是( ).
A.(-5,3) B.(1,3) C.(1,-3) D.(-5,-1)
8.线段MN是由线段EF经过平移得到的,若点E(-1,3)的对应点M(2,1),则点F (-3,-2)的对应点N的坐标是( )
A.(-1,0) B.(-6,0) C.(0,-4) D.(0,0)
9.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
10.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
二、填空题
11.如果将点A(-3,-1)向右平移2个单位长度,再向下平移3个单位得到点B,那么点B的坐标是________.
12.将点向左平移个单位长度后可得到对应点坐标是________;将点向上平移单位长度后可得对应点坐标是________.
13.一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作_________平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的_________;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
14.在平面直角坐标系中,把点A(2,3)向左平移一个单位得到点A′,则点A′的坐标为_____.
15.在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
(1)当a=1时,则点Q的坐标为____;
(2)当点P在直线上运动时,点Q也随之运动.当a=___时,AQ+BQ的值最小为____.
三、解答题
16.在学习完《位置与坐标》,小斌、小亮、小敏和小芳设计了一个游戏,他们在操场上画了如图所示,每小格边长均为的方格.若小斌从点出发,依次到点(小亮),(小敏),(小芳)处,规定:向北和向东走为正,向南和向西走为负如果从到记为,从到记为,数对中的第一个数表示东西方向,第二个数表示南北方向.
(1)图中的到,到分别记为______;
(2)若小斌的行走路线为,请计算小斌走过的路程;
(3)若小亮从点出发到点,行走的路线依次为,,请在图中标出点的位置;
(4)若图中有两个格点,,且点,,则应记为______.
17.如图所示,已知点A(2,1),B(8,2),C(6,3).
(1)若将△ABC向下平移 5个单位长度,再向左平移 9个单位长度,得到△ ′ ′ ′,画出平移后图形并写出各顶点的坐标.
(2)求△ABC的面积.
18.综合与实践(1)动手、计算:数学活动课上,在边长为1的小正方形组成的网格中建立如图1所示的平面直角坐标系,小明进行了下列操作研究图形的面积计算问题:将点向下平移5个单位长度,得到点,再将点向左平移4个单位长度,得到点,则点的坐标为:______,的面积为:______;(方法:直接计算)
(2)在图2中,线段的端点坐标、,将线段向下平移5个单位长度,得到线段,再将线段向左平移4个单位长度,得到线段,则四边形的面积为:______;(方法:直接计算)
总结规律:平移变换下可直接利用特殊图形的面积公式求面积.
(3)在图3中,线段的端点坐标、,将线段向下平移5个单位长度,得到线段,再将线段向左平移4个单位长度,得到线段,则四边形的面积为:______,(方法:间接计算)并写出算式.
总结规律:平移变换下当不容易直接计算图形的面积时,可利用面积的“割补”来完成计算.
参考答案
1.B
【详解】( 2, 3)向左平移2个单位长度得到的点的坐标是:( 4, 3).
故选B.
2.A
【详解】解:根据题意可建立如下所示平面直角坐标系,
A、中国馆的坐标为(-1,-2),故本选项正确;
B、国际馆的坐标为(3,-1),故本选项错误;
C、生活体验馆的坐标为(7,4),故本选项错误;
D、植物馆的坐标为(-7,-4),故本选项错误.
故选A.
3.D
【详解】由图可得,点A在O点北偏东50°方向,距O点3m的地方,
故选D.
4.A
【详解】解:∵将三角形三个顶点的横坐标都减2,纵坐标不变,
∴所得三角形与原三角形的关系是:将原图向左平移两个单位.
故选:A.
5.C
【详解】∵点A的坐标是(﹣1,2),作点A关于y轴的对称点,得到点A'
∴A′(1,2)
∵将点A'向下平移4个单位,得到点A″
∴点A″的坐标是:(1,﹣2)
故选C
6.C
经过观察分析可得每4个数的和为2,把100个数分为25组,即可得到相应结果.
详解:x1+x2+x3+x4=1-1-1+3=2;
x5+x6+x7+x8=3-3-3+5=2;
…
x97+x98+x99+x100=2;
∴原式=2×(100÷4)=50.
故选C.
7.B
∵A(-2,1)向上平移2个单位,再向右平移3个单位后得到B
∴1+2=3,-2+3=1
点B的坐标是(1,3)
故选B.
8.C
【详解】解:点E(-1,3)向右平移3个单位长度,向下移2个单位长度到M(2,1),所以点F(-3,-2)也向右平移3个单位长度,向下平移2个单位长度,得到点N(0,-4).
故选C.
9.B
【详解】跳蚤运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依次类推,到(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).
故选B.
10.B
【详解】由题意知(10,20)表示向东走10米,再向北走20米,故为B点.
故选:B.
11.解:将点A(-3,-1)向右平移2个单位长度再向下平移3个单位长度得到点B(-3+2,-1-3)
即(-1,-4),
故答案为:(-1,-4).
12. 解:(2,﹣5)向左平移3个单位长度后可得到对应点坐标是(﹣5,﹣5);
将点(2,+5)向上平移3单位长度后可得对应点坐标是(2,8).
故答案为(﹣5,﹣5)和(2,8).
13. 一次 变化
14.解:∵点A(2,3)向左平移1个单位长度,
∴点A′的横坐标为2-1=1,纵坐标不变,
∴A′的坐标为(1,3).
故答案为:(1,3).
15. (1)过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,如图1.∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°.∵∠APQ=90°,∴∠EPA=∠FPQ=90°﹣∠APF.在△PEA和△PFQ中,,∴△PEA≌△PFQ.∴PE=PF,EA=QF.∵a=1,∴P(1,3).∴OE=BP=1,PE=3.∵A(2,0),∴OA=2,∴EA=1.∴PF=3,QF=1.∴点Q的坐标为(4,4).
(2)若点P的坐标为(a,3),则PF=PE=3,QF=AE=|2﹣a|.∴点Q的坐标为(a+3,5﹣a).∵无论a为何值,点Q的坐标(a+3,5﹣a)都满足一次函数解析式y=﹣x+8,∴点Q始终在直线y=﹣x+8上运动.设直线y=﹣x+8与x轴、y轴分别交于点M、N,如图2所示.当x=0时y=8,当y=0时x=8.∴OM=ON=8.∵∠AOB=90°,∴∠OMN=45°.过点A关于直线MN作对称点A′,连A′Q、A′M,则A′Q=AQ,A′M=AM=6,∠A′MN=∠AMN=45°.∴∠A′MA=90°,AQ+BQ=A′Q+BQ.根据两点之间线段最短可知:当A′、Q、B三点共线时,AQ+BQ=A′Q+BQ最短,最小值为A′B长.设直线BP与A′M相交于点H,则BH⊥A′M.在Rt△A′HB中,∠A′HB=90,BH=OM=8,A′H=A′M﹣MH=6﹣3=3,∴A′B= ==.当A′、Q、B三点共线时,∵BN∥A′M,∴△BQN~△A′QM.根据相似三角形对应高的比等于相似比可得:,解得xQ=.∴a+3=.∴a=.∴当a=时,AQ+BQ的值最小为.
故答案为(1)(4,4);(2);.
16.(1)由题意,得,;
(2)
,
.
所以,小斌走过了.
(3)如图所示:
(4)∵点,,
∴为
即.
17.解:(1)根据题意,如图即为所求,
A’(-7,-4) ,B’(-1,-3) ,C’(-3,-2)
(2)S△ABC=62---=12-4-1-3=4
18.解:(1)由题意可得:A1(3,3)、A2(3,-2)、A3(-1,-2),
∴A1A2=5,A2A3=4,∠A1A2A3=90°,
∴△A1A2A3的面积=×4×5=10;
故填(-1,-2),10;
(2)由题意得:A1B1=3-1=2
∴四边形A1B1B3A3的面积为=2×4=8;
故填8;
(3)四边形A1B1B3A3的面积=.
故填13.
