02任意角的三角函数
图片预览


文档简介
02任意角的三角函数
1.任意角的三角函数的定义一
〖定义〗
HYPERLINK "http://www.21cnjy.com"
如图,设 HYPERLINK "http://www.21cnjy.com" 是一个任意角,它的终边上任意一点 HYPERLINK "http://www.21cnjy.com" ,它与原点的距离是 HYPERLINK "http://www.21cnjy.com" ,那么角 HYPERLINK "http://www.21cnjy.com" 的正弦、余弦、正切、余切、正割、余割分别记作:
正弦: HYPERLINK "http://www.21cnjy.com" ;余弦: HYPERLINK "http://www.21cnjy.com" ;
正切: HYPERLINK "http://www.21cnjy.com" ;余切: HYPERLINK "http://www.21cnjy.com" ;
正割: HYPERLINK "http://www.21cnjy.com" ;余割: HYPERLINK "http://www.21cnjy.com" .
这六个函数统称为三角函数。
详解:
〖概念辨析〗 HYPERLINK "http://www.21cnjy.com" 不是sin与α的乘积,它是一个整体,是一个确定的比值,是三角函数记号,其他五个三角函数也应同样理解。
实例:
〖特例〗要熟记的特殊角的三角函数
表一:
HYPERLINK "http://www.21cnjy.com"
表二:
HYPERLINK "http://www.21cnjy.com"
〖例题〗
例:已知角 HYPERLINK "http://www.21cnjy.com" 的终边经过点 HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的三角函数值.
解:因为 HYPERLINK "http://www.21cnjy.com" ,
所以 HYPERLINK "http://www.21cnjy.com" ,
于是
HYPERLINK "http://www.21cnjy.com" ;
HYPERLINK "http://www.21cnjy.com" ;
HYPERLINK "http://www.21cnjy.com"
2.任意角的三角函数的定义二
〖定义〗
HYPERLINK "http://www.21cnjy.com"
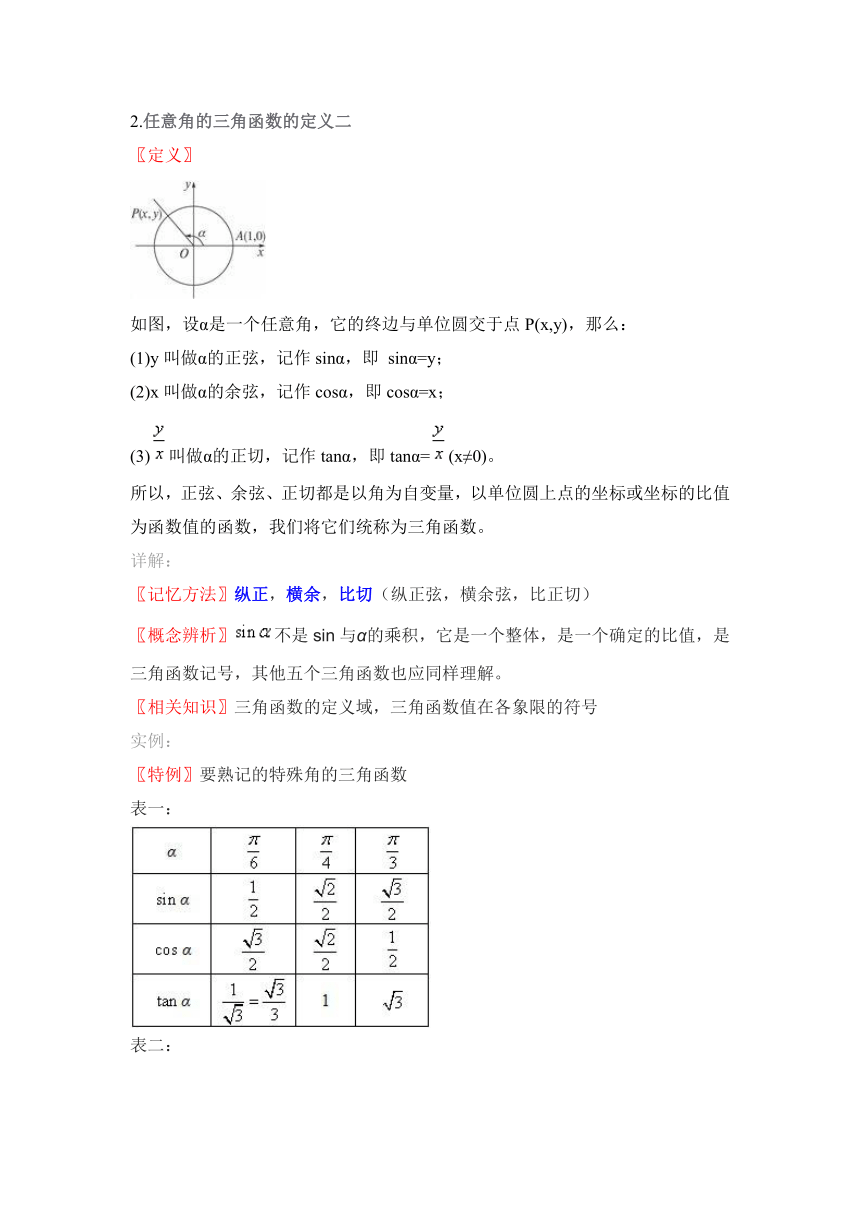
如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sinα,即 sinα=y;
(2)x叫做α的余弦,记作cosα,即cosα=x;
(3) HYPERLINK "http://www.21cnjy.com" 叫做α的正切,记作tanα,即tanα= HYPERLINK "http://www.21cnjy.com" (x≠0)。
所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
详解:
〖记忆方法〗纵正,横余,比切(纵正弦,横余弦,比正切)
〖概念辨析〗 HYPERLINK "http://www.21cnjy.com" 不是sin与α的乘积,它是一个整体,是一个确定的比值,是三角函数记号,其他五个三角函数也应同样理解。
〖相关知识〗三角函数的定义域,三角函数值在各象限的符号
实例:
〖特例〗要熟记的特殊角的三角函数
表一:
HYPERLINK "http://www.21cnjy.com"
表二:
HYPERLINK "http://www.21cnjy.com"
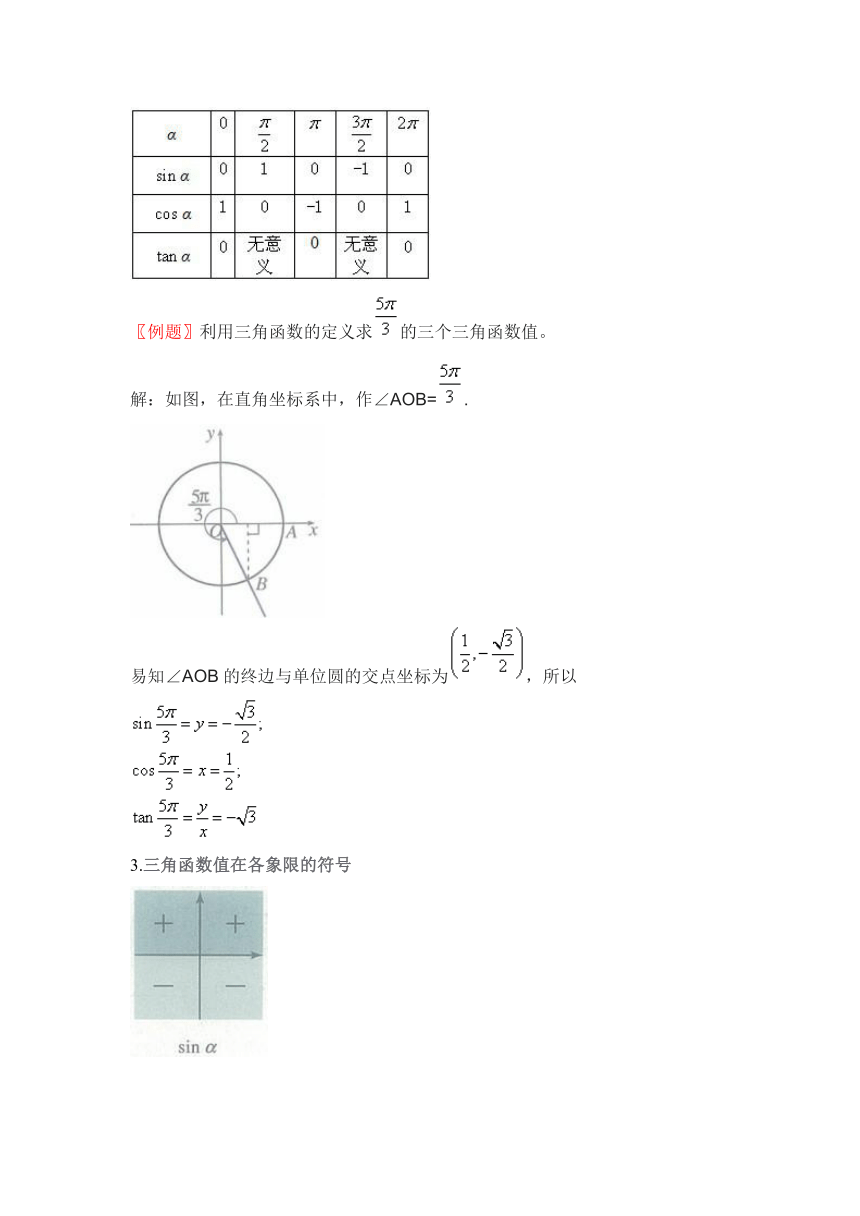
〖例题〗利用三角函数的定义求 HYPERLINK "http://www.21cnjy.com" 的三个三角函数值。
解:如图,在直角坐标系中,作∠AOB= HYPERLINK "http://www.21cnjy.com" .
HYPERLINK "http://www.21cnjy.com"
易知∠AOB的终边与单位圆的交点坐标为 HYPERLINK "http://www.21cnjy.com" ,所以
HYPERLINK "http://www.21cnjy.com"
3.三角函数值在各象限的符号
HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com"
详解:
〖记忆方法〗一全正,二正弦,三正切,四余 ( http: / / www.21cnjy.com )弦
〖概念辨析〗
在第一象限内,所有的三角函数值都为正值;
在第二象限内,正弦函数值为正值;
在第三象限内,正切函数值为正值;
在第四象限内,余弦函数值为正值。
〖相关知识〗任意角的三角函数的定义
实例:
〖例题〗确定下列三角函数值的符号:(1)sin 156°,(2) HYPERLINK "http://www.21cnjy.com" ;
(1)
HYPERLINK "http://www.21cnjy.com"
(2)
HYPERLINK "http://www.21cnjy.com"
4.三角函数的定义域和值域
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、确定三角函数的定义域时, ( http: / / www.21cnjy.com )应抓住分母等于零时比值无意义这一关键,结合三角函数的定义,可以得到三角函数的定义域和值域。
2、特别要引起注意的是正切函数的定义域
〖相关知识〗任意角的三角函数的定义
5.同角三角函数的基本关系式
〖代数表示〗
1.平方关系
HYPERLINK "http://www.21cnjy.com"
2.商数关系
HYPERLINK "http://www.21cnjy.com" ;
〖几何表示〗
HYPERLINK "http://www.21cnjy.com"
如图,在RT△OMP中,有 HYPERLINK "http://www.21cnjy.com" 。
详解:
〖记忆方法〗记忆方法、口诀
〖概念辨析〗
公式 HYPERLINK "http://www.21cnjy.com" (平方关系)和 HYPERLINK "http://www.21cnjy.com" (商数关系)称为同角三角函数的基本关系式。这里的同角有两层含义:一是“角相同”,二是对“任意”一个角(在使得函数有意义的前提下)关系式都成立。
〖相关知识〗任意角的三角函数的定义
实例:
〖例题〗
已知 HYPERLINK "http://www.21cnjy.com" ,且 HYPERLINK "http://www.21cnjy.com" 为第三象限角,求 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的值.
解: HYPERLINK "http://www.21cnjy.com" 为第三象限角
HYPERLINK "http://www.21cnjy.com"
〖应用〗
(1)“ HYPERLINK "http://www.21cnjy.com" ”代换法:即 HYPERLINK "http://www.21cnjy.com" 。如
HYPERLINK "http://www.21cnjy.com" 。
(2) 和积转化法: 同角正余弦间的和与积关系与转化的方法。如
HYPERLINK "http://www.21cnjy.com" ;
(3)弦切转化法:同角正弦与余弦的商可以转化为正切函数式的方法,即 HYPERLINK "http://www.21cnjy.com" 。
如
HYPERLINK "http://www.21cnjy.com"
(4)已知角的某一三角函数值,可以求其余的三角函数值,即“知一求二”法。在这过程中常常用到“平方关系”: HYPERLINK "http://www.21cnjy.com" 。计算时往往要开平方,要注意根据角所在的象限确定函数值的符号,若角所在象限不确定,则要就角可能所在的象限进行分类讨论。
1.任意角的三角函数的定义一
〖定义〗
HYPERLINK "http://www.21cnjy.com"
如图,设 HYPERLINK "http://www.21cnjy.com" 是一个任意角,它的终边上任意一点 HYPERLINK "http://www.21cnjy.com" ,它与原点的距离是 HYPERLINK "http://www.21cnjy.com" ,那么角 HYPERLINK "http://www.21cnjy.com" 的正弦、余弦、正切、余切、正割、余割分别记作:
正弦: HYPERLINK "http://www.21cnjy.com" ;余弦: HYPERLINK "http://www.21cnjy.com" ;
正切: HYPERLINK "http://www.21cnjy.com" ;余切: HYPERLINK "http://www.21cnjy.com" ;
正割: HYPERLINK "http://www.21cnjy.com" ;余割: HYPERLINK "http://www.21cnjy.com" .
这六个函数统称为三角函数。
详解:
〖概念辨析〗 HYPERLINK "http://www.21cnjy.com" 不是sin与α的乘积,它是一个整体,是一个确定的比值,是三角函数记号,其他五个三角函数也应同样理解。
实例:
〖特例〗要熟记的特殊角的三角函数
表一:
HYPERLINK "http://www.21cnjy.com"
表二:
HYPERLINK "http://www.21cnjy.com"
〖例题〗
例:已知角 HYPERLINK "http://www.21cnjy.com" 的终边经过点 HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的三角函数值.
解:因为 HYPERLINK "http://www.21cnjy.com" ,
所以 HYPERLINK "http://www.21cnjy.com" ,
于是
HYPERLINK "http://www.21cnjy.com" ;
HYPERLINK "http://www.21cnjy.com" ;
HYPERLINK "http://www.21cnjy.com"
2.任意角的三角函数的定义二
〖定义〗
HYPERLINK "http://www.21cnjy.com"
如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sinα,即 sinα=y;
(2)x叫做α的余弦,记作cosα,即cosα=x;
(3) HYPERLINK "http://www.21cnjy.com" 叫做α的正切,记作tanα,即tanα= HYPERLINK "http://www.21cnjy.com" (x≠0)。
所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
详解:
〖记忆方法〗纵正,横余,比切(纵正弦,横余弦,比正切)
〖概念辨析〗 HYPERLINK "http://www.21cnjy.com" 不是sin与α的乘积,它是一个整体,是一个确定的比值,是三角函数记号,其他五个三角函数也应同样理解。
〖相关知识〗三角函数的定义域,三角函数值在各象限的符号
实例:
〖特例〗要熟记的特殊角的三角函数
表一:
HYPERLINK "http://www.21cnjy.com"
表二:
HYPERLINK "http://www.21cnjy.com"
〖例题〗利用三角函数的定义求 HYPERLINK "http://www.21cnjy.com" 的三个三角函数值。
解:如图,在直角坐标系中,作∠AOB= HYPERLINK "http://www.21cnjy.com" .
HYPERLINK "http://www.21cnjy.com"
易知∠AOB的终边与单位圆的交点坐标为 HYPERLINK "http://www.21cnjy.com" ,所以
HYPERLINK "http://www.21cnjy.com"
3.三角函数值在各象限的符号
HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com"
详解:
〖记忆方法〗一全正,二正弦,三正切,四余 ( http: / / www.21cnjy.com )弦
〖概念辨析〗
在第一象限内,所有的三角函数值都为正值;
在第二象限内,正弦函数值为正值;
在第三象限内,正切函数值为正值;
在第四象限内,余弦函数值为正值。
〖相关知识〗任意角的三角函数的定义
实例:
〖例题〗确定下列三角函数值的符号:(1)sin 156°,(2) HYPERLINK "http://www.21cnjy.com" ;
(1)
HYPERLINK "http://www.21cnjy.com"
(2)
HYPERLINK "http://www.21cnjy.com"
4.三角函数的定义域和值域
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、确定三角函数的定义域时, ( http: / / www.21cnjy.com )应抓住分母等于零时比值无意义这一关键,结合三角函数的定义,可以得到三角函数的定义域和值域。
2、特别要引起注意的是正切函数的定义域
〖相关知识〗任意角的三角函数的定义
5.同角三角函数的基本关系式
〖代数表示〗
1.平方关系
HYPERLINK "http://www.21cnjy.com"
2.商数关系
HYPERLINK "http://www.21cnjy.com" ;
〖几何表示〗
HYPERLINK "http://www.21cnjy.com"
如图,在RT△OMP中,有 HYPERLINK "http://www.21cnjy.com" 。
详解:
〖记忆方法〗记忆方法、口诀
〖概念辨析〗
公式 HYPERLINK "http://www.21cnjy.com" (平方关系)和 HYPERLINK "http://www.21cnjy.com" (商数关系)称为同角三角函数的基本关系式。这里的同角有两层含义:一是“角相同”,二是对“任意”一个角(在使得函数有意义的前提下)关系式都成立。
〖相关知识〗任意角的三角函数的定义
实例:
〖例题〗
已知 HYPERLINK "http://www.21cnjy.com" ,且 HYPERLINK "http://www.21cnjy.com" 为第三象限角,求 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的值.
解: HYPERLINK "http://www.21cnjy.com" 为第三象限角
HYPERLINK "http://www.21cnjy.com"
〖应用〗
(1)“ HYPERLINK "http://www.21cnjy.com" ”代换法:即 HYPERLINK "http://www.21cnjy.com" 。如
HYPERLINK "http://www.21cnjy.com" 。
(2) 和积转化法: 同角正余弦间的和与积关系与转化的方法。如
HYPERLINK "http://www.21cnjy.com" ;
(3)弦切转化法:同角正弦与余弦的商可以转化为正切函数式的方法,即 HYPERLINK "http://www.21cnjy.com" 。
如
HYPERLINK "http://www.21cnjy.com"
(4)已知角的某一三角函数值,可以求其余的三角函数值,即“知一求二”法。在这过程中常常用到“平方关系”: HYPERLINK "http://www.21cnjy.com" 。计算时往往要开平方,要注意根据角所在的象限确定函数值的符号,若角所在象限不确定,则要就角可能所在的象限进行分类讨论。
