04三角函数的图像与性质
图片预览


文档简介
04三角函数的图像与性质
1.五点法
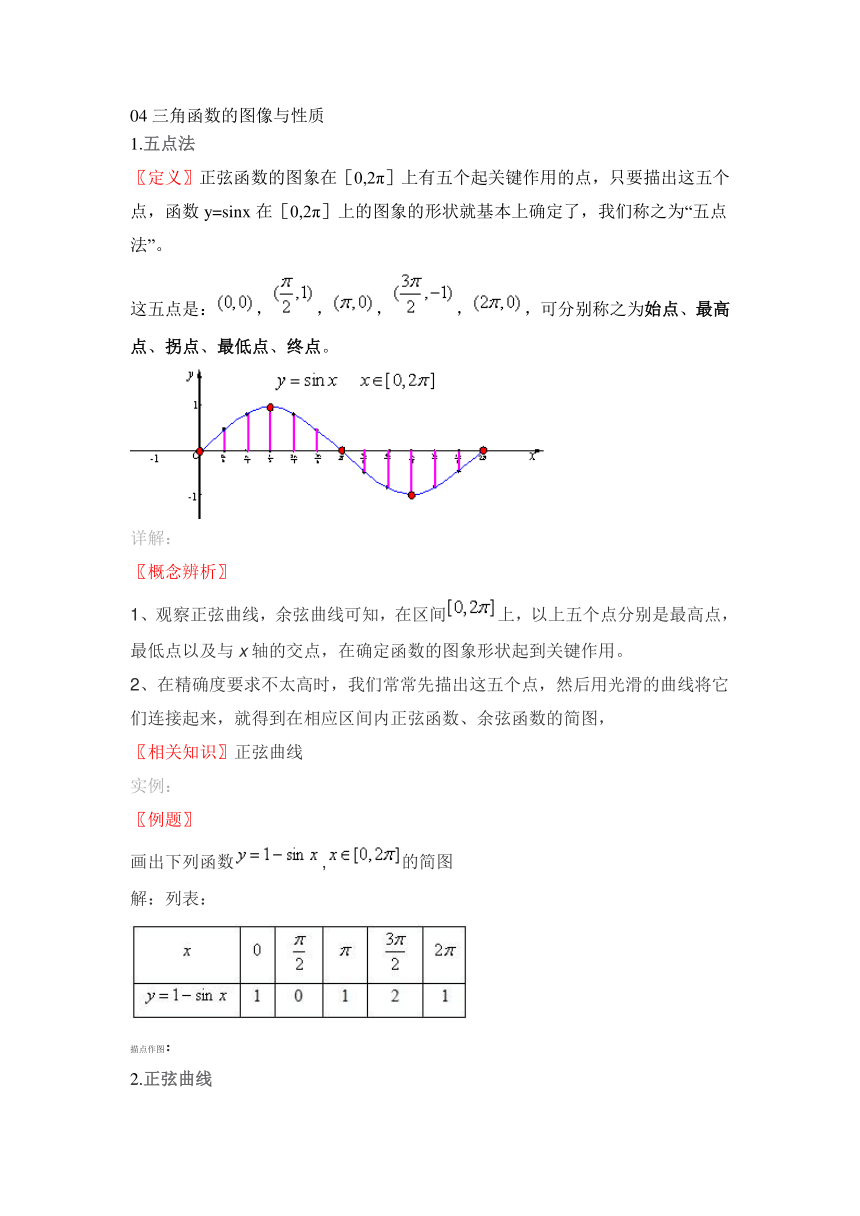
〖定义〗正弦函数的图象在[0,2π]上有五个起关键作用的点,只要描出这五个点,函数y=sinx在[0,2π]上的图象的形状就基本上确定了,我们称之为“五点法”。
这五点是: HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,可分别称之为始点、最高点、拐点、最低点、终点。
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、观察正弦曲线,余弦曲线可知,在区间 HYPERLINK "http://www.21cnjy.com" 上,以上五个点分别是最高点,最低点以及与x轴的交点,在确定函数的图象形状起到关键作用。
2、在精确度要求不太高时,我们常常先描出这五个点,然后用光滑的曲线将它们连接起来,就得到在相应区间内正弦函数、余弦函数的简图,
〖相关知识〗正弦曲线
实例:
〖例题〗
画出下列函数 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的简图
解:列表:
HYPERLINK "http://www.21cnjy.com"
描点作图:
2.正弦曲线
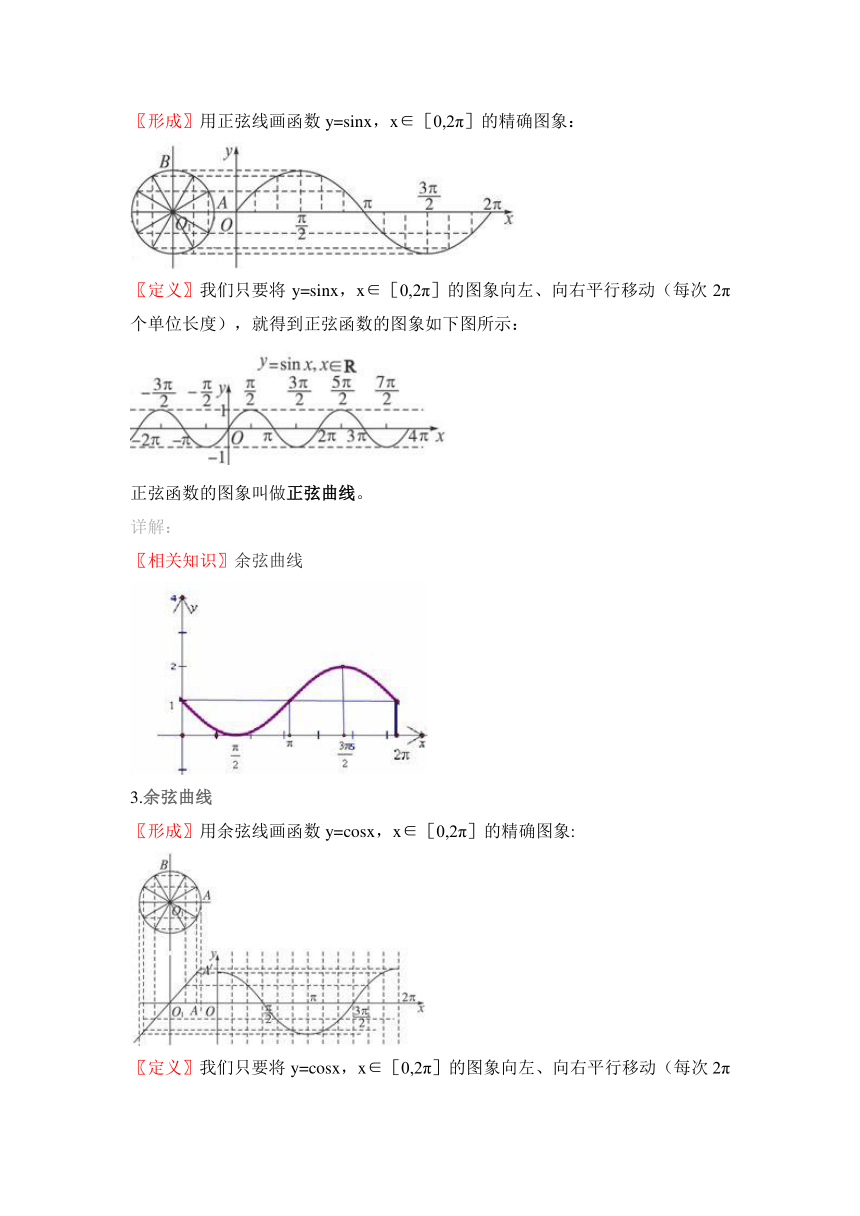
〖形成〗用正弦线画函数y=sinx,x∈[0,2π]的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=sinx,x∈[0,2π]的图象向左、向右平行移动(每次2π个单位长度),就得到正弦函数的图象如下图所示:
HYPERLINK "http://www.21cnjy.com"
正弦函数的图象叫做正弦曲线。
详解:
〖相关知识〗余弦曲线
HYPERLINK "http://www.21cnjy.com"
3.余弦曲线
〖形成〗用余弦线画函数y=cosx,x∈[0,2π]的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=cosx,x∈[0,2π]的图象向左、向右平行移动(每次2π个单位长度),就得到余弦函数的图象如下图所示
HYPERLINK "http://www.21cnjy.com"
余弦函数的图象叫做余弦曲线。
详解:
〖概念辨析〗
能否利用正弦曲线做出余弦函数的图象呢?
由诱导公式有 HYPERLINK "http://www.21cnjy.com" ,因此,将正弦函数的图象左移 HYPERLINK "http://www.21cnjy.com" 个单位,即得到余弦函数的图象。
〖相关知识〗正弦曲线
4.周期函数
〖定义〗对于函数 HYPERLINK "http://www.21cnjy.com" ,如果存在一个非零常数T,使得x取定义域内的任意值时,都有 HYPERLINK "http://www.21cnjy.com" 那么函数 HYPERLINK "http://www.21cnjy.com" 叫做周期函数。
其中非零常数T叫做这个函数的一个周期。
如果T中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期。
详解:
〖概念辨析〗
(1)对于函数 HYPERLINK "http://www.21cnjy.com" (其中 HYPERLINK "http://www.21cnjy.com" ),如果存在非零常数T,使得 HYPERLINK "http://www.21cnjy.com" 对定义域内的任何值都成立,那么这个函数的一个周期是 HYPERLINK "http://www.21cnjy.com" ,而不是T。
(2)所有的周期函数未必都有最小正周期,例如常数函数就不存在最小正周期。
〖相关知识〗正弦函数的图象,余弦函数的图象
实例:
〖特例〗
1、正弦、余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π。
2、正切函数也是周期函数, HYPERLINK "http://www.21cnjy.com" 都是它的周期,最小正周期是π。
〖常用结论〗
1.一般地,如果T( HYPERLINK "http://www.21cnjy.com" )是函数 HYPERLINK "http://www.21cnjy.com" 的一个周期,那么 HYPERLINK "http://www.21cnjy.com" 也是函数 HYPERLINK "http://www.21cnjy.com" 的一个周期。
2.若 HYPERLINK "http://www.21cnjy.com" 则2T是函数f(x)的一个周期。
因为 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
3.若 HYPERLINK "http://www.21cnjy.com" ,则2T是函数f(x)的一个周期。
因为 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
4.形如 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的函数,周期为 HYPERLINK "http://www.21cnjy.com" ;形如 HYPERLINK "http://www.21cnjy.com" 的函数,周期减半,即 HYPERLINK "http://www.21cnjy.com" ;形如 HYPERLINK "http://www.21cnjy.com" 的函数,周期为 HYPERLINK "http://www.21cnjy.com"
〖例题〗
例:求下列函数的周期: HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ∈R;
解:周期 HYPERLINK "http://www.21cnjy.com" (注释:根据公式 HYPERLINK "http://www.21cnjy.com" )
5.正弦函数、余弦函数的性质
正弦函数的性质如下:
HYPERLINK "http://www.21cnjy.com"
余弦函数的性质如下:
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、函数的性质是三角函数部分的重要内容,是解决三角函数有关问题的重要依据,记忆时,要结合三角函数的图象。
2、正弦函数、余弦函数都不是定义域上的单调函数。另外,说“正弦函数在第一象限是增函数”也是错误的,因为在第一象限,即使是终边相同的角,它们也可以相差 HYPERLINK "http://www.21cnjy.com" 的整数倍。
〖相关知识〗正弦函数的图象,余弦函数的图象,正切函数的性质
实例:
〖例题〗
例:利用函数的单调性比较下面两个三角函数值的大小:
sin103°15′与sin 164°30′;
解:因为函数 HYPERLINK "http://www.21cnjy.com" 在区间 HYPERLINK "http://www.21cnjy.com" 的范围内是单调递减的,又因为 HYPERLINK "http://www.21cnjy.com" ,所以 HYPERLINK "http://www.21cnjy.com"
6.正切曲线
〖形成〗用正切线画函数y=tanx, HYPERLINK "http://www.21cnjy.com" 的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=tanx, HYPERLINK "http://www.21cnjy.com" 的图象向左、向右平行移动(每次π个单位长度),就得到正切函数的图象如下图所示
HYPERLINK "http://www.21cnjy.com"
正切函数的图象叫做正切曲线。
详解:
〖概念辨析〗由图可以看出,正切曲线是被相互平行的直线 HYPERLINK "http://www.21cnjy.com" 所隔开的无穷多支曲线组成的。
〖相关7.正切函数的性质
正切函数的性质:
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1.正切函数 HYPERLINK "http://www.21cnjy.com" 是单调递增函数,但不能说函数在其定义域内是单调递增函数,正切函数无单调减区间。
3.判断函数奇偶性时,必须先检验定义域是否关于原点对称,如果是,再验证 HYPERLINK "http://www.21cnjy.com" 是否等于 HYPERLINK "http://www.21cnjy.com" 或 HYPERLINK "http://www.21cnjy.com" ,进而判断函数的奇偶性;如果不是,则该函数必是非奇非偶函数。
〖相关知识〗正切曲线,正弦函数、余弦函数的性质
实例:
〖例题〗
例:根据正切函数的图象,写出使下列不等式成立的 HYPERLINK "http://www.21cnjy.com" 的集合: HYPERLINK "http://www.21cnjy.com" ;
解:根据正切函数的图像如下图:
HYPERLINK "http://www.21cnjy.com"
由图可看出要使 HYPERLINK "http://www.21cnjy.com"
因为函数 HYPERLINK "http://www.21cnjy.com" 的图像是在每个区间是单调递增的,
不等式 HYPERLINK "http://www.21cnjy.com" 成立的x的集合是 HYPERLINK "http://www.21cnjy.com"
〖相关知识〗正切函数的性质
实例:
〖例题〗
例:根据正切函数的图象,写出使下列不等式成立的 HYPERLINK "http://www.21cnjy.com" 的集合: HYPERLINK "http://www.21cnjy.com" ;
解:根据正切函数的图像如下图:
HYPERLINK "http://www.21cnjy.com"
由图可看出要使 HYPERLINK "http://www.21cnjy.com"
因为函数 HYPERLINK "http://www.21cnjy.com" 的图像是在每个区间是单调递增的,
不等式 HYPERLINK "http://www.21cnjy.com" 成立的x的集合是 HYPERLINK "http://www.21cnjy.com"
1.五点法
〖定义〗正弦函数的图象在[0,2π]上有五个起关键作用的点,只要描出这五个点,函数y=sinx在[0,2π]上的图象的形状就基本上确定了,我们称之为“五点法”。
这五点是: HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,可分别称之为始点、最高点、拐点、最低点、终点。
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、观察正弦曲线,余弦曲线可知,在区间 HYPERLINK "http://www.21cnjy.com" 上,以上五个点分别是最高点,最低点以及与x轴的交点,在确定函数的图象形状起到关键作用。
2、在精确度要求不太高时,我们常常先描出这五个点,然后用光滑的曲线将它们连接起来,就得到在相应区间内正弦函数、余弦函数的简图,
〖相关知识〗正弦曲线
实例:
〖例题〗
画出下列函数 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的简图
解:列表:
HYPERLINK "http://www.21cnjy.com"
描点作图:
2.正弦曲线
〖形成〗用正弦线画函数y=sinx,x∈[0,2π]的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=sinx,x∈[0,2π]的图象向左、向右平行移动(每次2π个单位长度),就得到正弦函数的图象如下图所示:
HYPERLINK "http://www.21cnjy.com"
正弦函数的图象叫做正弦曲线。
详解:
〖相关知识〗余弦曲线
HYPERLINK "http://www.21cnjy.com"
3.余弦曲线
〖形成〗用余弦线画函数y=cosx,x∈[0,2π]的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=cosx,x∈[0,2π]的图象向左、向右平行移动(每次2π个单位长度),就得到余弦函数的图象如下图所示
HYPERLINK "http://www.21cnjy.com"
余弦函数的图象叫做余弦曲线。
详解:
〖概念辨析〗
能否利用正弦曲线做出余弦函数的图象呢?
由诱导公式有 HYPERLINK "http://www.21cnjy.com" ,因此,将正弦函数的图象左移 HYPERLINK "http://www.21cnjy.com" 个单位,即得到余弦函数的图象。
〖相关知识〗正弦曲线
4.周期函数
〖定义〗对于函数 HYPERLINK "http://www.21cnjy.com" ,如果存在一个非零常数T,使得x取定义域内的任意值时,都有 HYPERLINK "http://www.21cnjy.com" 那么函数 HYPERLINK "http://www.21cnjy.com" 叫做周期函数。
其中非零常数T叫做这个函数的一个周期。
如果T中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期。
详解:
〖概念辨析〗
(1)对于函数 HYPERLINK "http://www.21cnjy.com" (其中 HYPERLINK "http://www.21cnjy.com" ),如果存在非零常数T,使得 HYPERLINK "http://www.21cnjy.com" 对定义域内的任何值都成立,那么这个函数的一个周期是 HYPERLINK "http://www.21cnjy.com" ,而不是T。
(2)所有的周期函数未必都有最小正周期,例如常数函数就不存在最小正周期。
〖相关知识〗正弦函数的图象,余弦函数的图象
实例:
〖特例〗
1、正弦、余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π。
2、正切函数也是周期函数, HYPERLINK "http://www.21cnjy.com" 都是它的周期,最小正周期是π。
〖常用结论〗
1.一般地,如果T( HYPERLINK "http://www.21cnjy.com" )是函数 HYPERLINK "http://www.21cnjy.com" 的一个周期,那么 HYPERLINK "http://www.21cnjy.com" 也是函数 HYPERLINK "http://www.21cnjy.com" 的一个周期。
2.若 HYPERLINK "http://www.21cnjy.com" 则2T是函数f(x)的一个周期。
因为 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
3.若 HYPERLINK "http://www.21cnjy.com" ,则2T是函数f(x)的一个周期。
因为 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
4.形如 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的函数,周期为 HYPERLINK "http://www.21cnjy.com" ;形如 HYPERLINK "http://www.21cnjy.com" 的函数,周期减半,即 HYPERLINK "http://www.21cnjy.com" ;形如 HYPERLINK "http://www.21cnjy.com" 的函数,周期为 HYPERLINK "http://www.21cnjy.com"
〖例题〗
例:求下列函数的周期: HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ∈R;
解:周期 HYPERLINK "http://www.21cnjy.com" (注释:根据公式 HYPERLINK "http://www.21cnjy.com" )
5.正弦函数、余弦函数的性质
正弦函数的性质如下:
HYPERLINK "http://www.21cnjy.com"
余弦函数的性质如下:
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、函数的性质是三角函数部分的重要内容,是解决三角函数有关问题的重要依据,记忆时,要结合三角函数的图象。
2、正弦函数、余弦函数都不是定义域上的单调函数。另外,说“正弦函数在第一象限是增函数”也是错误的,因为在第一象限,即使是终边相同的角,它们也可以相差 HYPERLINK "http://www.21cnjy.com" 的整数倍。
〖相关知识〗正弦函数的图象,余弦函数的图象,正切函数的性质
实例:
〖例题〗
例:利用函数的单调性比较下面两个三角函数值的大小:
sin103°15′与sin 164°30′;
解:因为函数 HYPERLINK "http://www.21cnjy.com" 在区间 HYPERLINK "http://www.21cnjy.com" 的范围内是单调递减的,又因为 HYPERLINK "http://www.21cnjy.com" ,所以 HYPERLINK "http://www.21cnjy.com"
6.正切曲线
〖形成〗用正切线画函数y=tanx, HYPERLINK "http://www.21cnjy.com" 的精确图象:
HYPERLINK "http://www.21cnjy.com"
〖定义〗我们只要将y=tanx, HYPERLINK "http://www.21cnjy.com" 的图象向左、向右平行移动(每次π个单位长度),就得到正切函数的图象如下图所示
HYPERLINK "http://www.21cnjy.com"
正切函数的图象叫做正切曲线。
详解:
〖概念辨析〗由图可以看出,正切曲线是被相互平行的直线 HYPERLINK "http://www.21cnjy.com" 所隔开的无穷多支曲线组成的。
〖相关7.正切函数的性质
正切函数的性质:
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1.正切函数 HYPERLINK "http://www.21cnjy.com" 是单调递增函数,但不能说函数在其定义域内是单调递增函数,正切函数无单调减区间。
3.判断函数奇偶性时,必须先检验定义域是否关于原点对称,如果是,再验证 HYPERLINK "http://www.21cnjy.com" 是否等于 HYPERLINK "http://www.21cnjy.com" 或 HYPERLINK "http://www.21cnjy.com" ,进而判断函数的奇偶性;如果不是,则该函数必是非奇非偶函数。
〖相关知识〗正切曲线,正弦函数、余弦函数的性质
实例:
〖例题〗
例:根据正切函数的图象,写出使下列不等式成立的 HYPERLINK "http://www.21cnjy.com" 的集合: HYPERLINK "http://www.21cnjy.com" ;
解:根据正切函数的图像如下图:
HYPERLINK "http://www.21cnjy.com"
由图可看出要使 HYPERLINK "http://www.21cnjy.com"
因为函数 HYPERLINK "http://www.21cnjy.com" 的图像是在每个区间是单调递增的,
不等式 HYPERLINK "http://www.21cnjy.com" 成立的x的集合是 HYPERLINK "http://www.21cnjy.com"
〖相关知识〗正切函数的性质
实例:
〖例题〗
例:根据正切函数的图象,写出使下列不等式成立的 HYPERLINK "http://www.21cnjy.com" 的集合: HYPERLINK "http://www.21cnjy.com" ;
解:根据正切函数的图像如下图:
HYPERLINK "http://www.21cnjy.com"
由图可看出要使 HYPERLINK "http://www.21cnjy.com"
因为函数 HYPERLINK "http://www.21cnjy.com" 的图像是在每个区间是单调递增的,
不等式 HYPERLINK "http://www.21cnjy.com" 成立的x的集合是 HYPERLINK "http://www.21cnjy.com"
