05函数y=Asin(ωx+φ)的图像
文档属性
| 名称 | 05函数y=Asin(ωx+φ)的图像 |  | |
| 格式 | zip | ||
| 文件大小 | 139.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-04 15:02:45 | ||
图片预览




文档简介
05函数y=Asin(ωx+φ)的图像
1.“五点法”画函数y=Asin(ωx+φ)的图象
〖画法〗一般地,对函数 HYPERLINK "http://www.21cnjy.com" ,其“五点法”列表为:
HYPERLINK "http://www.21cnjy.com"
接着描点画图即可。
详解:
〖概念辨析〗注意 HYPERLINK "http://www.21cnjy.com"
〖相关知识〗五点法
实例:
〖例题〗
例:画出函数 HYPERLINK "http://www.21cnjy.com" 在长度为一个周期的闭区间上的简图
解:列表:
HYPERLINK "http://www.21cnjy.com"
描点作图:
HYPERLINK "http://www.21cnjy.com"
2.函数y=Asin(ωx+φ)的性质
〖形成〗
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、函数y=Asin(ωx+φ)的性质本质上是由y=sinx的性质推导而来的,所以要重点掌握y=sinx的性质;
2、特别注意,若 HYPERLINK "http://www.21cnjy.com" ,要利用诱导公式把它变为 HYPERLINK "http://www.21cnjy.com" ,便于函数性质的研究。
〖相关知识〗函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:求函数 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ∈[0, HYPERLINK "http://www.21cnjy.com" ]的单调递减区间.
解:令 HYPERLINK "http://www.21cnjy.com" ,
函数 HYPERLINK "http://www.21cnjy.com" 的单调递减区间为 HYPERLINK "http://www.21cnjy.com" ,
由 HYPERLINK "http://www.21cnjy.com" ,
得 HYPERLINK "http://www.21cnjy.com" 。
设 HYPERLINK "http://www.21cnjy.com" ,
则 HYPERLINK "http://www.21cnjy.com" 。
所以函数 HYPERLINK "http://www.21cnjy.com" 的单调递减区间为 HYPERLINK "http://www.21cnjy.com"
3.由函数y=Asin(ωx+φ)的图象求解析式的步骤
〖步骤〗
①看图,求出 HYPERLINK "http://www.21cnjy.com" 、周期T;
②由
HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,
求出A、B和 HYPERLINK "http://www.21cnjy.com" ;
③由题设条件,或特殊值、特殊点求得 HYPERLINK "http://www.21cnjy.com" ;
从而求得函数 HYPERLINK "http://www.21cnjy.com" 的解析式。
详解:
〖概念辨析〗关键是找特殊点代入。
〖相关知识〗五点法
实例:
〖例题〗
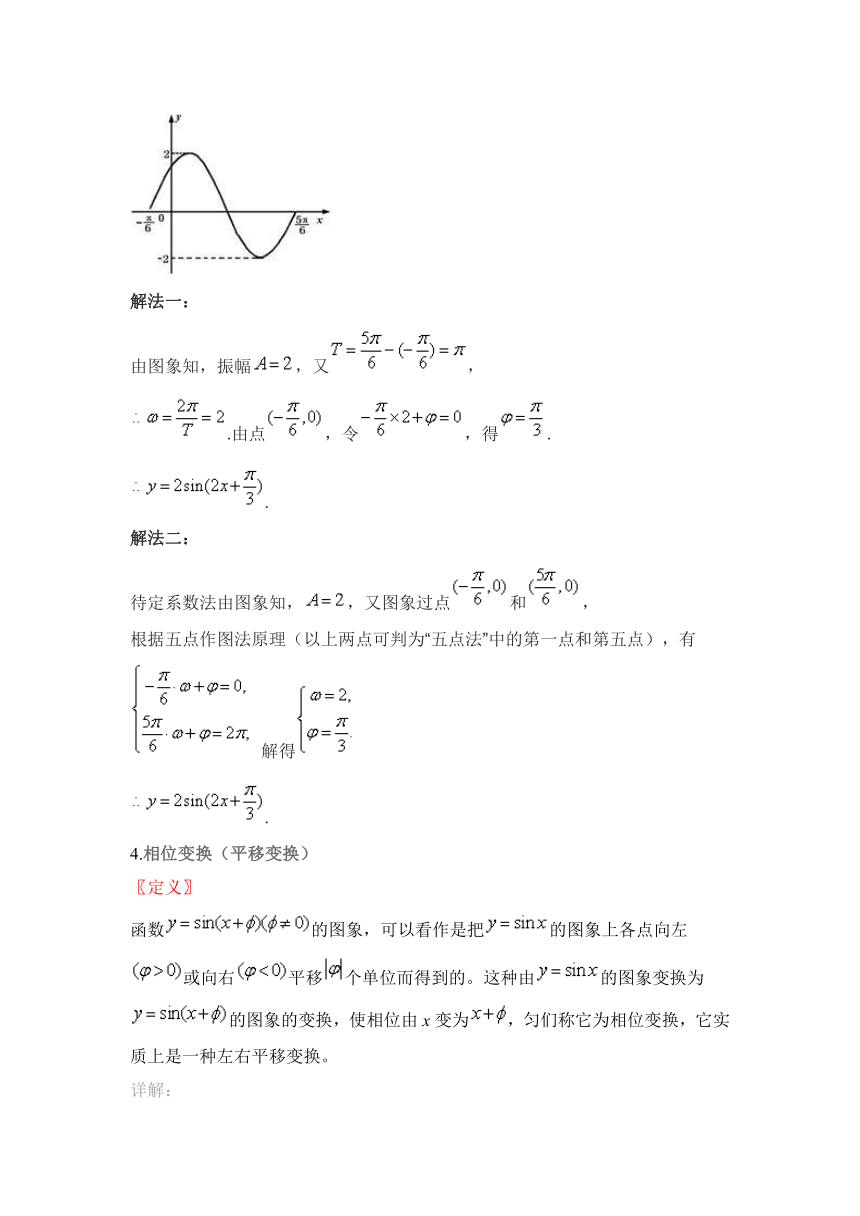
例:函数 HYPERLINK "http://www.21cnjy.com" 的一个周期内的图象如图,试确定 HYPERLINK "http://www.21cnjy.com" 的函数解析式.
HYPERLINK "http://www.21cnjy.com"
解法一:
由图象知,振幅 HYPERLINK "http://www.21cnjy.com" ,又 HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" .由点 HYPERLINK "http://www.21cnjy.com" ,令 HYPERLINK "http://www.21cnjy.com" ,得 HYPERLINK "http://www.21cnjy.com" .
HYPERLINK "http://www.21cnjy.com" .
解法二:
待定系数法由图象知, HYPERLINK "http://www.21cnjy.com" ,又图象过点 HYPERLINK "http://www.21cnjy.com" 和 HYPERLINK "http://www.21cnjy.com" ,
根据五点作图法原理(以上两点可判为“五点法”中的第一点和第五点),有 HYPERLINK "http://www.21cnjy.com" 解得 HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com" .
4.相位变换(平移变换)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点向左 HYPERLINK "http://www.21cnjy.com" 或向右 HYPERLINK "http://www.21cnjy.com" 平移 HYPERLINK "http://www.21cnjy.com" 个单位而得到的。这种由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象的变换,使相位由x变为 HYPERLINK "http://www.21cnjy.com" ,匀们称它为相位变换,它实质上是一种左右平移变换。
详解:
〖记忆方法〗左加右减
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把正弦曲线上所有的点向___平行移动___个单位长度.
解:向右平行移动 HYPERLINK "http://www.21cnjy.com" 个单位长度
5.周期变换(横向伸缩)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的横坐标都缩短 HYPERLINK "http://www.21cnjy.com" 或伸长 HYPERLINK "http://www.21cnjy.com" 到原来的 HYPERLINK "http://www.21cnjy.com" 倍(纵坐标不变)而得到的,由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象,其周期由 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" .这种变换叫做周期变换,它实质上是横向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的横坐标伸长到原来的____倍,纵坐标不变
解:由 HYPERLINK "http://www.21cnjy.com" 知,把余弦曲线上所有的点的横坐标伸长到原来的 HYPERLINK "http://www.21cnjy.com" 倍,纵坐标不变;
6.振幅变换
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的纵坐标都伸长 HYPERLINK "http://www.21cnjy.com" 或缩短 HYPERLINK "http://www.21cnjy.com" 到原来的A倍(横坐标不变)而得到的。这种变换叫做振幅变换,它实质上是纵向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗即题目
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的纵坐标缩短到原来的___,横坐标不变
解:纵坐标缩短到原来的 HYPERLINK "http://www.21cnjy.com" 倍,横坐标不变
5.周期变换(横向伸缩)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的横坐标都缩短 HYPERLINK "http://www.21cnjy.com" 或伸长 HYPERLINK "http://www.21cnjy.com" 到原来的 HYPERLINK "http://www.21cnjy.com" 倍(纵坐标不变)而得到的,由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象,其周期由 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" .这种变换叫做周期变换,它实质上是横向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的横坐标伸长到原来的____倍,纵坐标不变
解:由 HYPERLINK "http://www.21cnjy.com" 知,把余弦曲线上所有的点的横坐标伸长到原来的 HYPERLINK "http://www.21cnjy.com" 倍,纵坐标不变;
6.振幅变换
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的纵坐标都伸长 HYPERLINK "http://www.21cnjy.com" 或缩短 HYPERLINK "http://www.21cnjy.com" 到原来的A倍(横坐标不变)而得到的。这种变换叫做振幅变换,它实质上是纵向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗即题目
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的纵坐标缩短到原来的___,横坐标不变
解:纵坐标缩短到原来的 HYPERLINK "http://www.21cnjy.com" 倍,横坐标不变
7.用变换方法画函数y=Asin(ωx+φ)的图象
Ⅰ、先平移后伸缩:
其程序如下:
y=sinx的图象
HYPERLINK "http://www.21cnjy.com"
y=sin(x+φ)的图象
HYPERLINK "http://www.21cnjy.com"
y=sin(ωx+φ)的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx+φ)的图象。
Ⅱ、先伸缩后平移:
其程序如下:
y=sinx的图象
HYPERLINK "http://www.21cnjy.com"
y=Asinx的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx)的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx+φ)的图象。
详解:
〖辨析〗先伸缩再平移和先平移再伸缩本质的不同是平移的量不同了。
〖相关知识〗振幅变换、周期变换、平移变换
实例:
〖特例〗
HYPERLINK "http://www.21cnjy.com"
如上图,就是把 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" 的过程
〖例题〗
例:要得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需将函数 HYPERLINK "http://www.21cnjy.com" 的图象( )
A.向右平移 HYPERLINK "http://www.21cnjy.com" 个单位 B.向左平移 HYPERLINK "http://www.21cnjy.com" 个单位
C. 向左平移 HYPERLINK "http://www.21cnjy.com" 个单位 D.向右平移 HYPERLINK "http://www.21cnjy.com" 个单位
解: HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
∴只需将 HYPERLINK "http://www.21cnjy.com" 的图象向右平移 HYPERLINK "http://www.21cnjy.com" 个单位即可得到 HYPERLINK "http://www.21cnjy.com" 的图象。
故选A.
8.简谐运动的物理量
〖定义〗
当函数 HYPERLINK "http://www.21cnjy.com" 表示一个振动量时,
A称为振幅,它是做简谐运动的物体离开平衡位置的最大距离;
HYPERLINK "http://www.21cnjy.com" 称为周期,这是做简谐运动的物体往复运动一次所需要的时间;
HYPERLINK "http://www.21cnjy.com" 称为频率,它是做简谐运动的物体在单位时间内往复运动的次数;
HYPERLINK "http://www.21cnjy.com" 称为相位;
HYPERLINK "http://www.21cnjy.com" 时的相位φ称为初相。
详解:
〖相关知识〗振幅变换、周期变换、平移变换
实例:
〖例题〗
例:一根为Lcm的线,一端固定,另一端悬挂一个小球,组成一个单摆,小球摆动时,离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是 HYPERLINK "http://www.21cnjy.com" ,
(1)求小球摆动的周期和频率;
(2)已知g=980cm/s2,要使小球摆动的周期恰好是1秒,线的长度l应当是多少?
解:(1)
HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" .
1.“五点法”画函数y=Asin(ωx+φ)的图象
〖画法〗一般地,对函数 HYPERLINK "http://www.21cnjy.com" ,其“五点法”列表为:
HYPERLINK "http://www.21cnjy.com"
接着描点画图即可。
详解:
〖概念辨析〗注意 HYPERLINK "http://www.21cnjy.com"
〖相关知识〗五点法
实例:
〖例题〗
例:画出函数 HYPERLINK "http://www.21cnjy.com" 在长度为一个周期的闭区间上的简图
解:列表:
HYPERLINK "http://www.21cnjy.com"
描点作图:
HYPERLINK "http://www.21cnjy.com"
2.函数y=Asin(ωx+φ)的性质
〖形成〗
HYPERLINK "http://www.21cnjy.com"
详解:
〖概念辨析〗
1、函数y=Asin(ωx+φ)的性质本质上是由y=sinx的性质推导而来的,所以要重点掌握y=sinx的性质;
2、特别注意,若 HYPERLINK "http://www.21cnjy.com" ,要利用诱导公式把它变为 HYPERLINK "http://www.21cnjy.com" ,便于函数性质的研究。
〖相关知识〗函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:求函数 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ∈[0, HYPERLINK "http://www.21cnjy.com" ]的单调递减区间.
解:令 HYPERLINK "http://www.21cnjy.com" ,
函数 HYPERLINK "http://www.21cnjy.com" 的单调递减区间为 HYPERLINK "http://www.21cnjy.com" ,
由 HYPERLINK "http://www.21cnjy.com" ,
得 HYPERLINK "http://www.21cnjy.com" 。
设 HYPERLINK "http://www.21cnjy.com" ,
则 HYPERLINK "http://www.21cnjy.com" 。
所以函数 HYPERLINK "http://www.21cnjy.com" 的单调递减区间为 HYPERLINK "http://www.21cnjy.com"
3.由函数y=Asin(ωx+φ)的图象求解析式的步骤
〖步骤〗
①看图,求出 HYPERLINK "http://www.21cnjy.com" 、周期T;
②由
HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,
求出A、B和 HYPERLINK "http://www.21cnjy.com" ;
③由题设条件,或特殊值、特殊点求得 HYPERLINK "http://www.21cnjy.com" ;
从而求得函数 HYPERLINK "http://www.21cnjy.com" 的解析式。
详解:
〖概念辨析〗关键是找特殊点代入。
〖相关知识〗五点法
实例:
〖例题〗
例:函数 HYPERLINK "http://www.21cnjy.com" 的一个周期内的图象如图,试确定 HYPERLINK "http://www.21cnjy.com" 的函数解析式.
HYPERLINK "http://www.21cnjy.com"
解法一:
由图象知,振幅 HYPERLINK "http://www.21cnjy.com" ,又 HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" .由点 HYPERLINK "http://www.21cnjy.com" ,令 HYPERLINK "http://www.21cnjy.com" ,得 HYPERLINK "http://www.21cnjy.com" .
HYPERLINK "http://www.21cnjy.com" .
解法二:
待定系数法由图象知, HYPERLINK "http://www.21cnjy.com" ,又图象过点 HYPERLINK "http://www.21cnjy.com" 和 HYPERLINK "http://www.21cnjy.com" ,
根据五点作图法原理(以上两点可判为“五点法”中的第一点和第五点),有 HYPERLINK "http://www.21cnjy.com" 解得 HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com" .
4.相位变换(平移变换)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点向左 HYPERLINK "http://www.21cnjy.com" 或向右 HYPERLINK "http://www.21cnjy.com" 平移 HYPERLINK "http://www.21cnjy.com" 个单位而得到的。这种由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象的变换,使相位由x变为 HYPERLINK "http://www.21cnjy.com" ,匀们称它为相位变换,它实质上是一种左右平移变换。
详解:
〖记忆方法〗左加右减
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把正弦曲线上所有的点向___平行移动___个单位长度.
解:向右平行移动 HYPERLINK "http://www.21cnjy.com" 个单位长度
5.周期变换(横向伸缩)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的横坐标都缩短 HYPERLINK "http://www.21cnjy.com" 或伸长 HYPERLINK "http://www.21cnjy.com" 到原来的 HYPERLINK "http://www.21cnjy.com" 倍(纵坐标不变)而得到的,由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象,其周期由 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" .这种变换叫做周期变换,它实质上是横向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的横坐标伸长到原来的____倍,纵坐标不变
解:由 HYPERLINK "http://www.21cnjy.com" 知,把余弦曲线上所有的点的横坐标伸长到原来的 HYPERLINK "http://www.21cnjy.com" 倍,纵坐标不变;
6.振幅变换
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的纵坐标都伸长 HYPERLINK "http://www.21cnjy.com" 或缩短 HYPERLINK "http://www.21cnjy.com" 到原来的A倍(横坐标不变)而得到的。这种变换叫做振幅变换,它实质上是纵向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗即题目
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的纵坐标缩短到原来的___,横坐标不变
解:纵坐标缩短到原来的 HYPERLINK "http://www.21cnjy.com" 倍,横坐标不变
5.周期变换(横向伸缩)
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的横坐标都缩短 HYPERLINK "http://www.21cnjy.com" 或伸长 HYPERLINK "http://www.21cnjy.com" 到原来的 HYPERLINK "http://www.21cnjy.com" 倍(纵坐标不变)而得到的,由 HYPERLINK "http://www.21cnjy.com" 的图象变换为 HYPERLINK "http://www.21cnjy.com" 的图象,其周期由 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" .这种变换叫做周期变换,它实质上是横向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的横坐标伸长到原来的____倍,纵坐标不变
解:由 HYPERLINK "http://www.21cnjy.com" 知,把余弦曲线上所有的点的横坐标伸长到原来的 HYPERLINK "http://www.21cnjy.com" 倍,纵坐标不变;
6.振幅变换
〖定义〗
函数 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的图象,可以看作是把 HYPERLINK "http://www.21cnjy.com" 的图象上各点的纵坐标都伸长 HYPERLINK "http://www.21cnjy.com" 或缩短 HYPERLINK "http://www.21cnjy.com" 到原来的A倍(横坐标不变)而得到的。这种变换叫做振幅变换,它实质上是纵向的伸缩。
详解:
〖相关知识〗由函数y=Asin(ωx+φ)的图象
实例:
〖例题〗即题目
例:为了得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需把余弦曲线上所有的点的纵坐标缩短到原来的___,横坐标不变
解:纵坐标缩短到原来的 HYPERLINK "http://www.21cnjy.com" 倍,横坐标不变
7.用变换方法画函数y=Asin(ωx+φ)的图象
Ⅰ、先平移后伸缩:
其程序如下:
y=sinx的图象
HYPERLINK "http://www.21cnjy.com"
y=sin(x+φ)的图象
HYPERLINK "http://www.21cnjy.com"
y=sin(ωx+φ)的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx+φ)的图象。
Ⅱ、先伸缩后平移:
其程序如下:
y=sinx的图象
HYPERLINK "http://www.21cnjy.com"
y=Asinx的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx)的图象
HYPERLINK "http://www.21cnjy.com"
y=Asin(ωx+φ)的图象。
详解:
〖辨析〗先伸缩再平移和先平移再伸缩本质的不同是平移的量不同了。
〖相关知识〗振幅变换、周期变换、平移变换
实例:
〖特例〗
HYPERLINK "http://www.21cnjy.com"
如上图,就是把 HYPERLINK "http://www.21cnjy.com" 变为 HYPERLINK "http://www.21cnjy.com" 的过程
〖例题〗
例:要得到函数 HYPERLINK "http://www.21cnjy.com" 的图象,只需将函数 HYPERLINK "http://www.21cnjy.com" 的图象( )
A.向右平移 HYPERLINK "http://www.21cnjy.com" 个单位 B.向左平移 HYPERLINK "http://www.21cnjy.com" 个单位
C. 向左平移 HYPERLINK "http://www.21cnjy.com" 个单位 D.向右平移 HYPERLINK "http://www.21cnjy.com" 个单位
解: HYPERLINK "http://www.21cnjy.com"
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
∴只需将 HYPERLINK "http://www.21cnjy.com" 的图象向右平移 HYPERLINK "http://www.21cnjy.com" 个单位即可得到 HYPERLINK "http://www.21cnjy.com" 的图象。
故选A.
8.简谐运动的物理量
〖定义〗
当函数 HYPERLINK "http://www.21cnjy.com" 表示一个振动量时,
A称为振幅,它是做简谐运动的物体离开平衡位置的最大距离;
HYPERLINK "http://www.21cnjy.com" 称为周期,这是做简谐运动的物体往复运动一次所需要的时间;
HYPERLINK "http://www.21cnjy.com" 称为频率,它是做简谐运动的物体在单位时间内往复运动的次数;
HYPERLINK "http://www.21cnjy.com" 称为相位;
HYPERLINK "http://www.21cnjy.com" 时的相位φ称为初相。
详解:
〖相关知识〗振幅变换、周期变换、平移变换
实例:
〖例题〗
例:一根为Lcm的线,一端固定,另一端悬挂一个小球,组成一个单摆,小球摆动时,离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是 HYPERLINK "http://www.21cnjy.com" ,
(1)求小球摆动的周期和频率;
(2)已知g=980cm/s2,要使小球摆动的周期恰好是1秒,线的长度l应当是多少?
解:(1)
HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" .
