2022--2023学年人教版八年级数学下册18.1.2平行四边形的四种判定课件(共19张PPT)
文档属性
| 名称 | 2022--2023学年人教版八年级数学下册18.1.2平行四边形的四种判定课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 18:03:34 | ||
图片预览




文档简介
(共19张PPT)
平行四边形的判定
学习
目标
01
掌握平行四边形的四种判定方法(重点)
02
掌握利用平行四边形的判定解决应用问题(难点)
复习
1.平行四边形除了对边平行,有哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
边:
角:
对角线:
问:这些逆命题是否都成立?我们如何去证明?
2.平行四边形上面的三条性质的逆命题各是什么?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
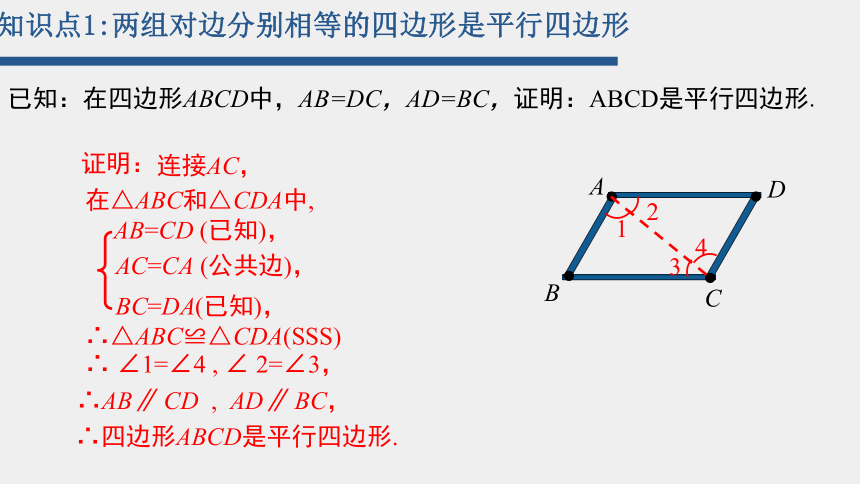
知识点1:两组对边分别相等的四边形是平行四边形
已知:在四边形ABCD中,AB=DC,AD=BC,证明:ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
结论一
两组对边分别相等的四边形是平行四边形.
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理1:
格式:
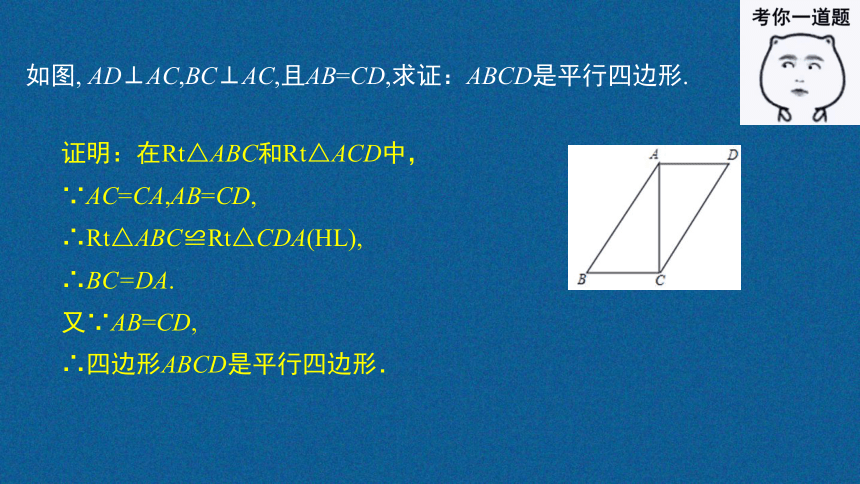
如图, AD⊥AC,BC⊥AC,且AB=CD,求证:ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
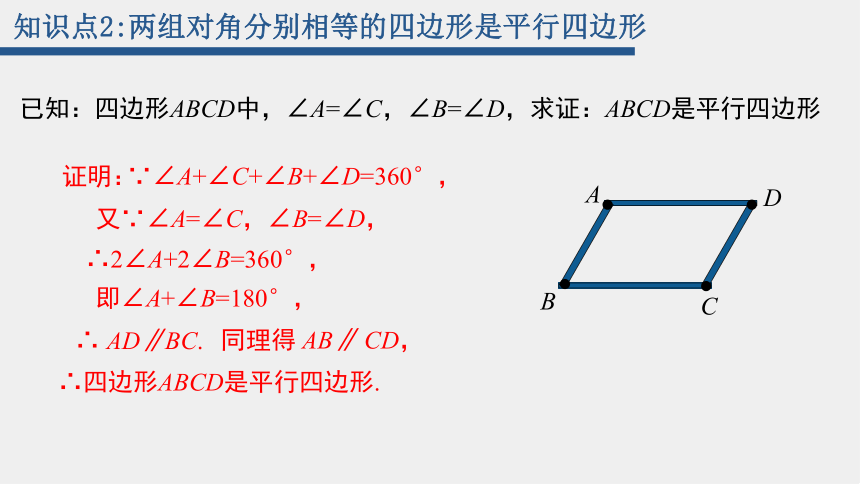
知识点2:两组对角分别相等的四边形是平行四边形
已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:ABCD是平行四边形
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
结论二
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理2:
格式:
如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
知识点3:对角线相互平分的四边形是平行四边形
如图,将两根细木条AC、BD的中点重叠并固定在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,观察四边形ABCD的形状?
B
D
O
A
C
通过上述的动画,我们猜想:
对角线相互平分的四边形是平行四边形
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.求证:ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS),
∴ ∠BAO=∠OCD , ∠ABO=∠CDO,
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
证明:
结论三
平行线的判定定理3:
格式:
对角线互相平分的四边形是平行四边形.
在四边形ABCD中
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
B
O
D
A
C
E
F
O
课堂练习
1.判断:
(1)有一组对边平行的四边形是平行四边形. ( )
(2)有两条边相等,并且另外的两条边也相等的四边
形一定是平行四边形. ( )
(3)对角线互相平分的四边形是平行四边形. ( )
(4)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(5)有一组对角相等且一组对边平行的四边形是平行
四边形. ( )
√
×
×
×
√
2.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
3.如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
B
D
A
C
6
4
4.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
A
B
C
D
E
P
5.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
6.如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.
01两组对边分别相等的四边形是平行四边形
02两组对角分别相等的四边形是平行四边形
03对角线互相平分的四边形是平行四边形
课堂小结
平行四边形的判定
学习
目标
01
掌握平行四边形的四种判定方法(重点)
02
掌握利用平行四边形的判定解决应用问题(难点)
复习
1.平行四边形除了对边平行,有哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
边:
角:
对角线:
问:这些逆命题是否都成立?我们如何去证明?
2.平行四边形上面的三条性质的逆命题各是什么?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
知识点1:两组对边分别相等的四边形是平行四边形
已知:在四边形ABCD中,AB=DC,AD=BC,证明:ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
结论一
两组对边分别相等的四边形是平行四边形.
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理1:
格式:
如图, AD⊥AC,BC⊥AC,且AB=CD,求证:ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
知识点2:两组对角分别相等的四边形是平行四边形
已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:ABCD是平行四边形
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
结论二
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理2:
格式:
如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
知识点3:对角线相互平分的四边形是平行四边形
如图,将两根细木条AC、BD的中点重叠并固定在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,观察四边形ABCD的形状?
B
D
O
A
C
通过上述的动画,我们猜想:
对角线相互平分的四边形是平行四边形
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.求证:ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS),
∴ ∠BAO=∠OCD , ∠ABO=∠CDO,
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
证明:
结论三
平行线的判定定理3:
格式:
对角线互相平分的四边形是平行四边形.
在四边形ABCD中
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
B
O
D
A
C
E
F
O
课堂练习
1.判断:
(1)有一组对边平行的四边形是平行四边形. ( )
(2)有两条边相等,并且另外的两条边也相等的四边
形一定是平行四边形. ( )
(3)对角线互相平分的四边形是平行四边形. ( )
(4)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(5)有一组对角相等且一组对边平行的四边形是平行
四边形. ( )
√
×
×
×
√
2.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
3.如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
B
D
A
C
6
4
4.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
A
B
C
D
E
P
5.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
6.如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.
01两组对边分别相等的四边形是平行四边形
02两组对角分别相等的四边形是平行四边形
03对角线互相平分的四边形是平行四边形
课堂小结
