第六章 变量之间的关系[下学期]
图片预览

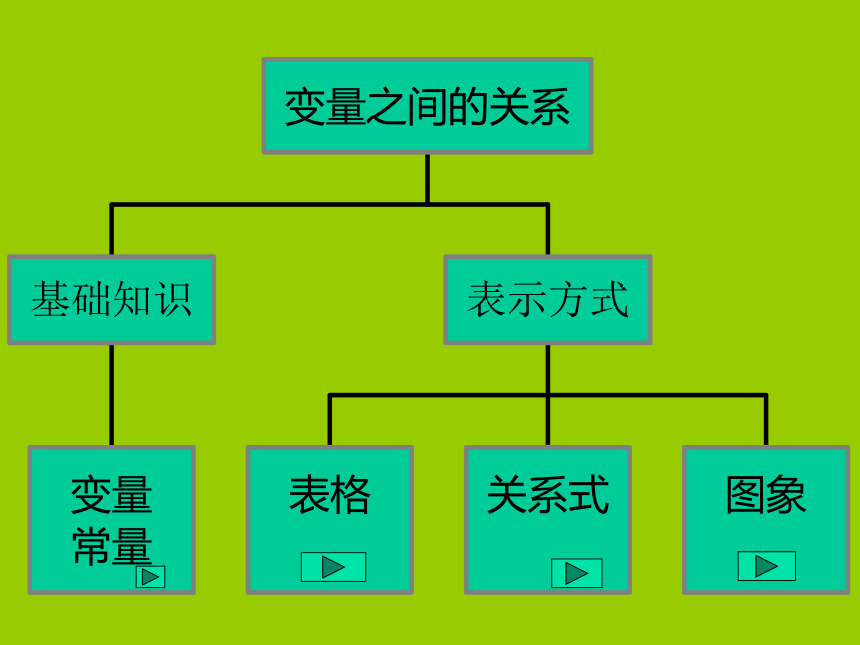







文档简介
课件22张PPT。变量之间的关系练习一:
1、树上落下的果子的高度随时间的变化而变化,这里时间是 ,果子的高度是 。2、小明骑自行车的速度是10km/小时,那么小明骑车所走的路程随时间的变化而变化 ,这里自变量是 ,因变量是 。自变量因变量小明骑车的时间小明骑车所走的路程什么是自变量?什么是因变量?比如:小王家距离学校2000米,小王每小时步行500米,X小时后小明距离学校Y米,这里的常量是 ,变量是 ,自变量是 ,因变量是 。练习二:
3、用总长为80米的绳索围成一个矩形,所围成的矩形的面积S(m2)随着矩形的一边长x(m)的变化而变化。
在这个变化中,变量是 ,常量是 ,自变量是 ,因变量是 。在某一变化过程中保持不变的量叫常量。小王家离学校2000米;小王步行速度500米/小时时间(X)和小王离学校的距离(Y)时间(X)小王离学校的距离(Y)面积S(m2)和边长x(m)总长为80米的绳索边长x(m)面积S(m2)一、表 格1、借助表格可以感知因变量随自变量变化的情况。
2、从表格中可以获取一些信息,能作出某种预测或估计。变量的表示方法例一:小红帮妈妈预算4月份的用电量,她记录了4月份初连续8天每天早上电表的读数,列成了表格如下:
(1)这个表格反映哪两个变量之间的关系?哪个是 自变量?哪个是因变量?(2)4月5 日早上电表的读数是多少?(3)这个月的前5 天共用电多少?(小红家每天只在晚上用电)
(4)估计4月9日早上电表的读数是多少?(5)估计4月份的总用电量。变量的表示方法日期与电表读数日期是自变量,电表读数是因变量。
读数是3539 - 21=18,即这个月的前5天共用电18千瓦时。
读数为49或50。
(46 - 21)÷7×30≈107。二、关 系 式1、能根据题意列简单的关系式。
2、能利用关系式进行简单的计算。变量的表示方法例2:
1、一个长方形的宽是8米,则这个长方形的面积y(cm2)与长x(cm)的关系式是 .
2、用总长为60cm的铁丝围成长方形,如果长方形的一边长为 a(cm),面积为 S (cm2)。
(1)说出这个变化中的自变量、因变量、常量。
(2)写出反映 a 与 S 之间的关系式。
(3)利用所写的关系式计算当a=12时,S的值是多少?变量的表示方法y = 8x自变量:长方形的边长因变量:面积常量:总长60cmS=a(30-a)S=2161、一棵小树高45 cm,每个月长3 cm,则x个月后树高y与x的关系式是 。
练习2、如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系式应该是( )A、y = 12x B、y = 18x C、y = xD、y = x Y = 45 + 3xD三、图象1、识别图象是否正确。
2、利用图象尽可能地获取自变量、因变量的信息。变量的表示方法例三:小明的父母出去散步,从家走(匀速)了20分钟到了一个离家900米的报亭,母亲因有事即按原速、原路返回。父亲看了10分钟报纸后,用了15分钟返回家。下图中哪一个是表示父亲离家的时间与距离之间的关系的图象?哪一个表示母亲离家的时间与距离之间关系的图象?ABCD答案:父亲(D)
母亲(B)
你答对了吗? 2.如图,我国人口统计图如下:人口总数随着时间的变化趋势是 ,估计2009年我国人口总数大概是 。逐渐增加13亿4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )B 1、如图,反映了一次运动会中的 项目的比赛, 先到达终点,其最快速度约是 。A9.1米/秒例四:下图所示的曲线表示某人骑自行车离家的距离与时间的关系,骑车者九时离开家,十五时回到家,根据这个曲线图,回答下列总问题。2、何时开始第一次休息?休息多长时间?
3、第一次休息时离家多远?
4、11:00到12:00他骑了多少千米?
5、他在9:00到10:00和10:00到
10:30的平均速度是多少?
6、他在何时到何时停止前进并休息用午餐?
7、他在停止前进后的返回途中,骑了多少
千米?返回时的平均速度是多少?1、到达离家最远的地方是什么时间?离家多远?ABCDEF2、某种油箱容量为60升的汽车,加满汽油后,汽车行驶
时油箱的油量Q(升)随汽车行驶时间t(时)变化的
关系式 如下:Q=60-6t
(1) 请完成下表 :(2) 汽车行驶5小时后,油箱中油量是__________升 4854303624巩固:(3)若汽车行驶中油箱油量为12升,
则汽车行驶了_________小时 (4)贮满60升汽油的汽车,
最多行驶__________小时 A 某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t810巩固:1.有一幢大楼,高12层,其中:一楼层高为4.5米,二楼及上楼层的层高均为3米,当楼房的层数发生变化时,楼高也随之发生变化.
(1)在这个变化过程中,自变量与因变量各是什么?
(2)设层数为x层(x为正整数),楼高为y(米),求y与x之间的关系式;
(3)当楼层由1变化到10时,楼高是怎样变化的?说说你的理由.3.假定甲,乙两人在一次赛跑中,离终点的距离s(米)与时间t(秒)的关系如图所示.问
(1)这是一次多少米的赛跑?
(2)甲,乙两人跑完全程分别用了多少时间?
(3)甲,乙两人谁先达到终点?
(4)乙在这次赛跑中的速度是多少?4.一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2米,达到坡底时达到40米/秒
(1)在这个变化过程中,自变量与因变量各是什么?
(2)求小球速度v(米/秒)与时间t(秒)之间的关系式;
(3)求经过3.5秒时小球的速度;
(4)当t在允许值范围内每增加1时,v是如何变化的?说你的理由.
(5)试一试,你能求出自变量t的取值范围吗?6.王凯上午9时骑自行车离开家,下午3时回到家,他离家的距离随时间的变化情况如图所示
(1)他到达离家最远的地方是什么时间?
离家多少远?
(2)他何时第一次停驶?
此时离家有多远?
(3)他由离家最远的地方
返回时的平均速度是多少?下课再见
1、树上落下的果子的高度随时间的变化而变化,这里时间是 ,果子的高度是 。2、小明骑自行车的速度是10km/小时,那么小明骑车所走的路程随时间的变化而变化 ,这里自变量是 ,因变量是 。自变量因变量小明骑车的时间小明骑车所走的路程什么是自变量?什么是因变量?比如:小王家距离学校2000米,小王每小时步行500米,X小时后小明距离学校Y米,这里的常量是 ,变量是 ,自变量是 ,因变量是 。练习二:
3、用总长为80米的绳索围成一个矩形,所围成的矩形的面积S(m2)随着矩形的一边长x(m)的变化而变化。
在这个变化中,变量是 ,常量是 ,自变量是 ,因变量是 。在某一变化过程中保持不变的量叫常量。小王家离学校2000米;小王步行速度500米/小时时间(X)和小王离学校的距离(Y)时间(X)小王离学校的距离(Y)面积S(m2)和边长x(m)总长为80米的绳索边长x(m)面积S(m2)一、表 格1、借助表格可以感知因变量随自变量变化的情况。
2、从表格中可以获取一些信息,能作出某种预测或估计。变量的表示方法例一:小红帮妈妈预算4月份的用电量,她记录了4月份初连续8天每天早上电表的读数,列成了表格如下:
(1)这个表格反映哪两个变量之间的关系?哪个是 自变量?哪个是因变量?(2)4月5 日早上电表的读数是多少?(3)这个月的前5 天共用电多少?(小红家每天只在晚上用电)
(4)估计4月9日早上电表的读数是多少?(5)估计4月份的总用电量。变量的表示方法日期与电表读数日期是自变量,电表读数是因变量。
读数是3539 - 21=18,即这个月的前5天共用电18千瓦时。
读数为49或50。
(46 - 21)÷7×30≈107。二、关 系 式1、能根据题意列简单的关系式。
2、能利用关系式进行简单的计算。变量的表示方法例2:
1、一个长方形的宽是8米,则这个长方形的面积y(cm2)与长x(cm)的关系式是 .
2、用总长为60cm的铁丝围成长方形,如果长方形的一边长为 a(cm),面积为 S (cm2)。
(1)说出这个变化中的自变量、因变量、常量。
(2)写出反映 a 与 S 之间的关系式。
(3)利用所写的关系式计算当a=12时,S的值是多少?变量的表示方法y = 8x自变量:长方形的边长因变量:面积常量:总长60cmS=a(30-a)S=2161、一棵小树高45 cm,每个月长3 cm,则x个月后树高y与x的关系式是 。
练习2、如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系式应该是( )A、y = 12x B、y = 18x C、y = xD、y = x Y = 45 + 3xD三、图象1、识别图象是否正确。
2、利用图象尽可能地获取自变量、因变量的信息。变量的表示方法例三:小明的父母出去散步,从家走(匀速)了20分钟到了一个离家900米的报亭,母亲因有事即按原速、原路返回。父亲看了10分钟报纸后,用了15分钟返回家。下图中哪一个是表示父亲离家的时间与距离之间的关系的图象?哪一个表示母亲离家的时间与距离之间关系的图象?ABCD答案:父亲(D)
母亲(B)
你答对了吗? 2.如图,我国人口统计图如下:人口总数随着时间的变化趋势是 ,估计2009年我国人口总数大概是 。逐渐增加13亿4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )B 1、如图,反映了一次运动会中的 项目的比赛, 先到达终点,其最快速度约是 。A9.1米/秒例四:下图所示的曲线表示某人骑自行车离家的距离与时间的关系,骑车者九时离开家,十五时回到家,根据这个曲线图,回答下列总问题。2、何时开始第一次休息?休息多长时间?
3、第一次休息时离家多远?
4、11:00到12:00他骑了多少千米?
5、他在9:00到10:00和10:00到
10:30的平均速度是多少?
6、他在何时到何时停止前进并休息用午餐?
7、他在停止前进后的返回途中,骑了多少
千米?返回时的平均速度是多少?1、到达离家最远的地方是什么时间?离家多远?ABCDEF2、某种油箱容量为60升的汽车,加满汽油后,汽车行驶
时油箱的油量Q(升)随汽车行驶时间t(时)变化的
关系式 如下:Q=60-6t
(1) 请完成下表 :(2) 汽车行驶5小时后,油箱中油量是__________升 4854303624巩固:(3)若汽车行驶中油箱油量为12升,
则汽车行驶了_________小时 (4)贮满60升汽油的汽车,
最多行驶__________小时 A 某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t810巩固:1.有一幢大楼,高12层,其中:一楼层高为4.5米,二楼及上楼层的层高均为3米,当楼房的层数发生变化时,楼高也随之发生变化.
(1)在这个变化过程中,自变量与因变量各是什么?
(2)设层数为x层(x为正整数),楼高为y(米),求y与x之间的关系式;
(3)当楼层由1变化到10时,楼高是怎样变化的?说说你的理由.3.假定甲,乙两人在一次赛跑中,离终点的距离s(米)与时间t(秒)的关系如图所示.问
(1)这是一次多少米的赛跑?
(2)甲,乙两人跑完全程分别用了多少时间?
(3)甲,乙两人谁先达到终点?
(4)乙在这次赛跑中的速度是多少?4.一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2米,达到坡底时达到40米/秒
(1)在这个变化过程中,自变量与因变量各是什么?
(2)求小球速度v(米/秒)与时间t(秒)之间的关系式;
(3)求经过3.5秒时小球的速度;
(4)当t在允许值范围内每增加1时,v是如何变化的?说你的理由.
(5)试一试,你能求出自变量t的取值范围吗?6.王凯上午9时骑自行车离开家,下午3时回到家,他离家的距离随时间的变化情况如图所示
(1)他到达离家最远的地方是什么时间?
离家多少远?
(2)他何时第一次停驶?
此时离家有多远?
(3)他由离家最远的地方
返回时的平均速度是多少?下课再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
