5.5 圆环的面积(课件)-六年级上册数学人教版(共25张PPT)
文档属性
| 名称 | 5.5 圆环的面积(课件)-六年级上册数学人教版(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 14:12:34 | ||
图片预览





文档简介
(共25张PPT)
你知道这些是什么形状吗?它们都有哪些特征?
学习目标
理解和掌握圆环的面积计算公式,并能用它
解决实际问题。
自学指导1
请同学们结合生活中常见的物品,比如一卷胶带,指一指,说一说,什么是圆环?
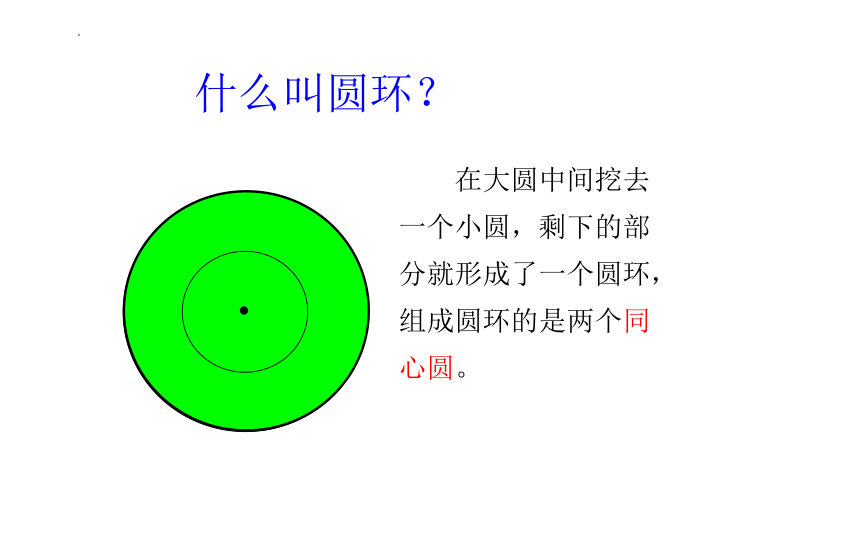
什么是圆环?
认识环形
两个同心圆之间的部分叫做环形,也叫圆环。
同心圆
r
R
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
·
·
·
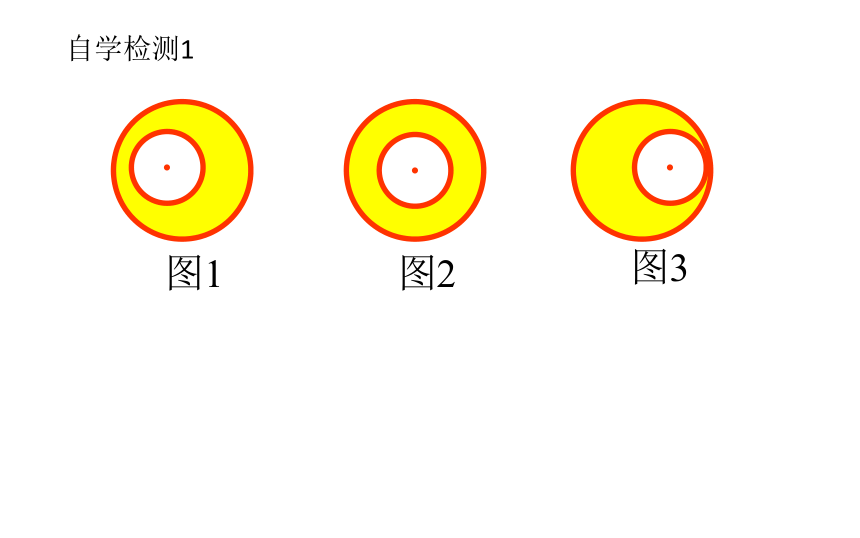
图1
图2
图3
自学检测1
·
图2
自学指导2
1、在同一圆环中,外圆的半径和内圆的半径有什么关系?
2、圆环的面积怎么求?
画圆环
r
R
r
R
第一步:求外圆的面积
第二步:求内圆的面积
求圆环的面积
S
环
S
外
S
内
= 外圆面积 – 内圆面积
圆环的面积
第三步:求环形的面积
πr
2
πR
2
S
外
S
内
-
光盘的银色部分是一个圆环,内圆半径
是2cm,外圆半径是6cm。它的面积是
多少?
2cm
6cm
2
3.14×6
=3.14 ×36
2
3.14×2
=3.14 ×4
113.04 - 12.56
=113.04 ( )
2
cm
=12.56 ( )
2
cm
=100.48 ( )
2
cm
例2
请找出下面圆环的内圆半径(r)或外圆半径(R):
8厘米
R=( )厘米
8厘米
2厘米
r=( )厘米
6厘米
4厘米
r=( )厘米
3厘米
1厘米
R=( )厘米
4
2
2
4
自学检测2
求下面圆环的面积
r=5cm
R=8cm
2
3.14×8
=3.14 ×64
2
3.14×5
=3.14 ×25
200.96 - 78.5
=200.96 ( )
2
cm
=78.5 ( )
2
cm
=122.46 ( )
2
cm
第一步:求外圆的面积
第二步:求内圆的面积
S
环
= 外圆面积 – 内圆面积
圆环的面积
第三步:求环形的面积
-πr
2
=πR
2
= S
外
- S
内
- r )
2
=π( R
2
S
环
- r )
2
=π( R
2
降2
加4
加3
减1
加3
求下面圆环的面积
r=5cm
R=8cm
=3.14 ×( 64 - 25 )
2
3.14×( 8
- 5 )
2
=3.14 ×39
=122.46 ( )
2
cm
当堂训练
3米
2米
某社区修建一个圆形花坛,半径是3米,在花坛周围又修了一条2米的环形小路。小路的面积是多少平方米?
一个圆形环岛的直径是50m,中间是一个花坛直径为10m的圆形花坛,其它地方是草坪。草坪的占地面积是多少?
3.14×(50÷2)2 - 3.14×(10÷2)2
= 3.14×625- 3.14×25
= 1962.5 – 78.5
= 1884(m2)
3.14×[(50÷2)2 – (10÷2)2]
= 3.14×[252 – 52]
= 3.14×[625 - 25]
= 1884(m2)
= 3.14×252 - 3.14×52
= 3.14×600
10米
50米
天圆地方
在中国古代,人们认为天是圆形的,像一把张开的大伞覆盖在地上,地是方形的,像一个棋盘。这一学说被称为“天圆地方”说。
学情分析
学生已经具备测量一般图形(物体)周长的技能,会计算长方形、正方形、三角形、平行四边形、梯形等图形的周长和面积,知道圆的特征,但是长方形、正方形、三角形、平行四边形、梯形等都是直线图形,而圆是曲线图形,在测量圆的周长和面积时,跟前面用到的方法有显著的不同。由此,教学将从对直线图形的研究,对学生而言是一种跨越与挑战。学生在实践活动中,独立完成有一定的难度,教师可以组织学生小组合作,并适当加以指导和启发。
板书设计
教学反思
本节课内容在教科书上只安排了一道例题作为圆面积的计算方法的应用。在教学时,教师从学生熟悉的情境出发,让他们认识圆环,知道圆环的组成,再教学例题,接着选择有层次性的练习,通过变式、求圆环的周长与面积对比练习使学生加深对圆环的认识突出解决问题的灵活性,培养学生结合实际分析图形解决问题的能力。整节课教学内容充实、丰富,教学效果好。
辅导策略
共性共同探讨、差生单独辅导
交流收获
数学基于练习,一定要加强练习,共性问题共同探讨、个性问题个别解决。
你知道这些是什么形状吗?它们都有哪些特征?
学习目标
理解和掌握圆环的面积计算公式,并能用它
解决实际问题。
自学指导1
请同学们结合生活中常见的物品,比如一卷胶带,指一指,说一说,什么是圆环?
什么是圆环?
认识环形
两个同心圆之间的部分叫做环形,也叫圆环。
同心圆
r
R
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
·
·
·
图1
图2
图3
自学检测1
·
图2
自学指导2
1、在同一圆环中,外圆的半径和内圆的半径有什么关系?
2、圆环的面积怎么求?
画圆环
r
R
r
R
第一步:求外圆的面积
第二步:求内圆的面积
求圆环的面积
S
环
S
外
S
内
= 外圆面积 – 内圆面积
圆环的面积
第三步:求环形的面积
πr
2
πR
2
S
外
S
内
-
光盘的银色部分是一个圆环,内圆半径
是2cm,外圆半径是6cm。它的面积是
多少?
2cm
6cm
2
3.14×6
=3.14 ×36
2
3.14×2
=3.14 ×4
113.04 - 12.56
=113.04 ( )
2
cm
=12.56 ( )
2
cm
=100.48 ( )
2
cm
例2
请找出下面圆环的内圆半径(r)或外圆半径(R):
8厘米
R=( )厘米
8厘米
2厘米
r=( )厘米
6厘米
4厘米
r=( )厘米
3厘米
1厘米
R=( )厘米
4
2
2
4
自学检测2
求下面圆环的面积
r=5cm
R=8cm
2
3.14×8
=3.14 ×64
2
3.14×5
=3.14 ×25
200.96 - 78.5
=200.96 ( )
2
cm
=78.5 ( )
2
cm
=122.46 ( )
2
cm
第一步:求外圆的面积
第二步:求内圆的面积
S
环
= 外圆面积 – 内圆面积
圆环的面积
第三步:求环形的面积
-πr
2
=πR
2
= S
外
- S
内
- r )
2
=π( R
2
S
环
- r )
2
=π( R
2
降2
加4
加3
减1
加3
求下面圆环的面积
r=5cm
R=8cm
=3.14 ×( 64 - 25 )
2
3.14×( 8
- 5 )
2
=3.14 ×39
=122.46 ( )
2
cm
当堂训练
3米
2米
某社区修建一个圆形花坛,半径是3米,在花坛周围又修了一条2米的环形小路。小路的面积是多少平方米?
一个圆形环岛的直径是50m,中间是一个花坛直径为10m的圆形花坛,其它地方是草坪。草坪的占地面积是多少?
3.14×(50÷2)2 - 3.14×(10÷2)2
= 3.14×625- 3.14×25
= 1962.5 – 78.5
= 1884(m2)
3.14×[(50÷2)2 – (10÷2)2]
= 3.14×[252 – 52]
= 3.14×[625 - 25]
= 1884(m2)
= 3.14×252 - 3.14×52
= 3.14×600
10米
50米
天圆地方
在中国古代,人们认为天是圆形的,像一把张开的大伞覆盖在地上,地是方形的,像一个棋盘。这一学说被称为“天圆地方”说。
学情分析
学生已经具备测量一般图形(物体)周长的技能,会计算长方形、正方形、三角形、平行四边形、梯形等图形的周长和面积,知道圆的特征,但是长方形、正方形、三角形、平行四边形、梯形等都是直线图形,而圆是曲线图形,在测量圆的周长和面积时,跟前面用到的方法有显著的不同。由此,教学将从对直线图形的研究,对学生而言是一种跨越与挑战。学生在实践活动中,独立完成有一定的难度,教师可以组织学生小组合作,并适当加以指导和启发。
板书设计
教学反思
本节课内容在教科书上只安排了一道例题作为圆面积的计算方法的应用。在教学时,教师从学生熟悉的情境出发,让他们认识圆环,知道圆环的组成,再教学例题,接着选择有层次性的练习,通过变式、求圆环的周长与面积对比练习使学生加深对圆环的认识突出解决问题的灵活性,培养学生结合实际分析图形解决问题的能力。整节课教学内容充实、丰富,教学效果好。
辅导策略
共性共同探讨、差生单独辅导
交流收获
数学基于练习,一定要加强练习,共性问题共同探讨、个性问题个别解决。
