2014学年度黑龙江省大庆市房顶中学北师大初三下数学期中试卷含答案
文档属性
| 名称 | 2014学年度黑龙江省大庆市房顶中学北师大初三下数学期中试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-03 10:18:02 | ||
图片预览


文档简介
2014年度大庆市房顶中学第二学期初三数学期中试卷
(考试时间90分钟)
一.选择题(共14小题,每小题3分)
1.由于受H7N9禽流感的影响,今年4月 ( http: / / www.21cnjy.com )份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤5元,下列所列方程中正确的是( )
A. 12(1+a%)2=5 B. 12(1﹣a%)2=5 C. 12(1﹣2a%)=5 D. 12(1﹣a2%)=5
2.将代数式x2+6x+2化成(x+p)2+q的形式为( )
A. (x﹣3)2+11 B. (x+3)2﹣7 C. (x+3)2﹣11 D. (x+2)2+4
3.一元二次方程x2+2x+2=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 只有一个实数根 D. 无实数根
4.三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )
A. 14 B. 12 C. 12或14 D. 以上都不对
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
5题图 6题图 7题图 8题图
5.如图,是用4个相同的小矩形与1个小正方 ( http: / / www.21cnjy.com )形镶嵌而成的正方形图案,已知该图案的面积为49,小正方形的面积为4,若用x,y表示小矩形的两边长(x>y),请观察图案,指出以下关系式中不正确的是( )
A. x+y=7 B. x﹣y=2 C. x2+y2=25 D. 4xy+4=49
6.如图,在△ABC中,∠ABC和∠ACB ( http: / / www.21cnjy.com )的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
A. 6 B. 7 C. 8 D. 9
7.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A. 50 B. 62 C. 65 D. 68
8.如图,过边长为3的等边 ( http: / / www.21cnjy.com )△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交边AC于点D,则DE的长为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. 不能确定
9.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( )
A. 6 B. 4 C. 3 D. 2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
9题图 11题图 12题图 14题图
10.下列说法中错误的是( )
A. 平行四边形的对角线互相平分
B. 有两对邻角互补的四边形为平行四边形
C. 对角线互相平分的四边形是平行四边形
D. 一组对边平行,一组对角相等的四边形是平行四边形
11.如图,等腰梯形ABCD中,AD∥BC,AB=DC,AD=3,AB=4,∠B=60°,则梯形的面积是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
12.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A. 100° B. 105° C. 110° D. 120°
13.下列各组条件中,能判定四边形ABCD为矩形的是( )
A. ∠A+∠B=90° B. AB∥CD,AB=CD,AC=BD
C. AB∥CD,AD=BC,AC=BD D. AC=BD,∠A=90°
14.如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是( )
A. b=a+c B. b=ac C. b2=a2+c2 D. b=2a=2c
二.填空题(共6小题,每小题3分)
15.若 ( http: / / www.21cnjy.com ),且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是_________.
16.已知x1、x2是方程2x2+14x﹣16=0的两实数根,那么 ( http: / / www.21cnjy.com )的值为 _________ .
17.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17题图 18题图 19题图
18.如图,在Rt△ABC中,∠C=9 ( http: / / www.21cnjy.com )0°,作AB的垂直平分线,交AB于D,交AC于E,连接BE.已知∠CBE=40°,则∠A= _________ 度.
19.如图,∠ABD、∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为 _________ .
20.关于x的方程mx2+3x=x2+4是一元二次方程,则m应满足条件是 _________ .
三.解答题(共6小题)
21.(每小题4分)
(1)用配方法解一元二次方程:3x2﹣6x﹣1=0;
(2)化简 ( http: / / www.21cnjy.com )
(3) ( http: / / www.21cnjy.com ) (4)2x2﹣7x+3=0.
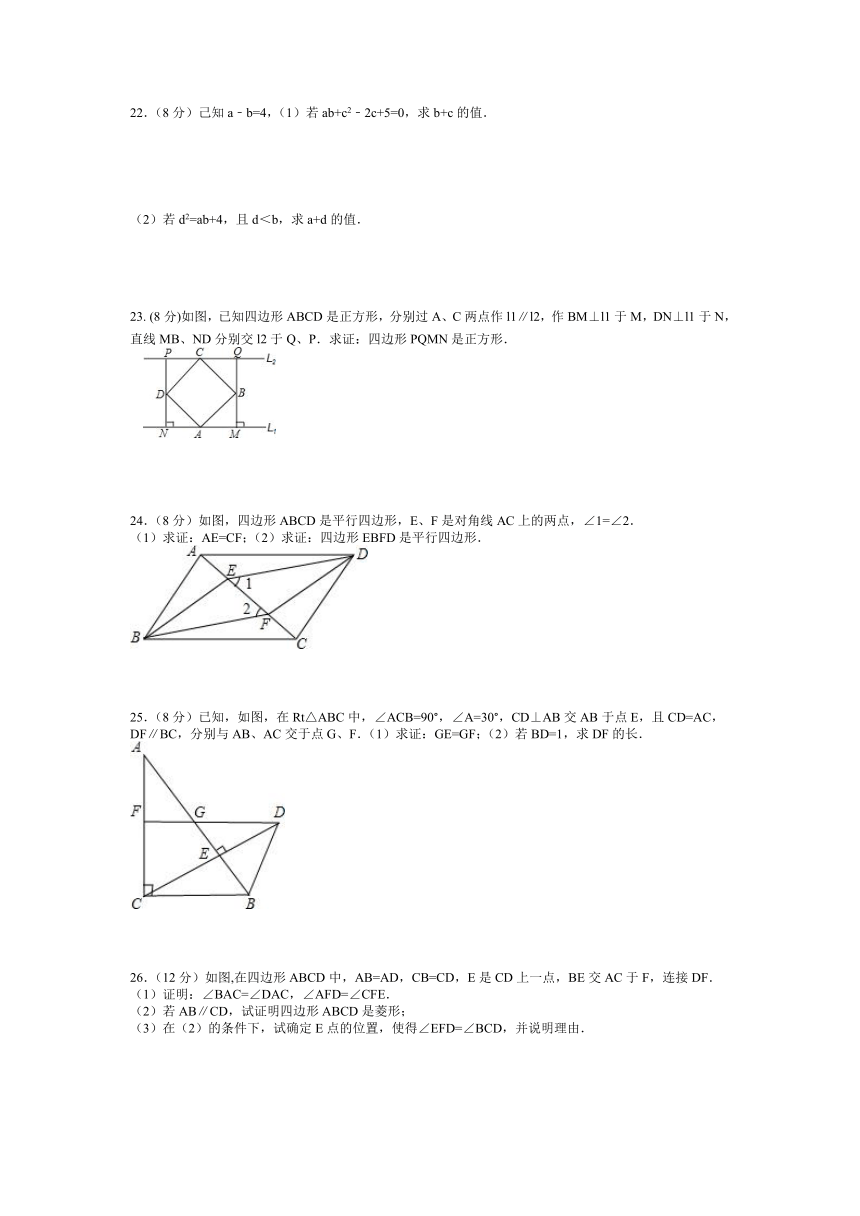
22.(8分)己知a﹣b=4,(1)若ab+c2﹣2c+5=0,求b+c的值.
(2)若d2=ab+4,且d<b,求a+d的值.
23. (8分)如图,已知四边形A ( http: / / www.21cnjy.com )BCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.
( http: / / www.21cnjy.com )
24.(8分)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;(2)求证:四边形EBFD是平行四边形.
( http: / / www.21cnjy.com )
25.(8分)已知,如图,在Rt△ ( http: / / www.21cnjy.com )ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.(1)求证:GE=GF;(2)若BD=1,求DF的长.
( http: / / www.21cnjy.com )
26.(12分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.
( http: / / www.21cnjy.com )
2014年度大庆市房顶中学第二学期初三数学期中试卷
答案
一.选择题(共14小题)
1.B
2.B
3.D
4.B
5.C
6.D
7.A
8.B
9.B
10.B
11.A
12.A
13.B
14.A
二.填空题(共6小题)
15. k≤4且k≠0 .
16. ﹣ ( http: / / www.21cnjy.com ) .
17. ( http: / / www.21cnjy.com ) .
18. 25
19. 20° .
20. m≠1 .
三.解答题(共6小题)
21.(1)x1= ( http: / / www.21cnjy.com ),x2= ( http: / / www.21cnjy.com );
(2)x+1
(3)x1=﹣2+ ( http: / / www.21cnjy.com ),x2=﹣2﹣ ( http: / / www.21cnjy.com ),x3=0,x4=﹣2
(4)x1=3, ( http: / / www.21cnjy.com ).
22.(1)b+c=﹣1(2)a+d=2
23
( http: / / www.21cnjy.com )
24.解答: (1)证明:如图:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠3=∠4,∵∠1=∠3+∠5,∠2=∠4+∠6,∴∠1=∠2∴∠5=∠6∵在△ADE与△CBF中, ( http: / / www.21cnjy.com )∴△ADE≌△CBF(ASA),∴AE=CF;(2))证明:∵∠1=∠2,∴DE∥BF.又∵由(1)知△ADE≌△CBF,∴DE=BF,∴四边形EBFD是平行四边形. ( http: / / www.21cnjy.com )
25.解答: (1)证明:∵DF∥BC,∠ACB=90°,∴∠CFD=90°.∵CD⊥AB,∴∠AEC=90°.在Rt△AEC和Rt△DFC中,∠AEC=∠CFD=90°,∠ACE=∠DCF,DC=AC,∴Rt△AEC≌Rt△DFC.∴CE=CF.∴DE=AF.而∠AGF=∠DGE,∠AFG=∠DEG=90°,∴Rt△AFG≌Rt△DEG.∴GF=GE.(2)解:∵CD⊥AB,∠A=30°,∴CE= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com )CD.∴CE=ED.∴BC=BD=1.又∵∠ECB+∠ACE=90°,∠A+∠ACE=90°,∴∠ECB=∠A=30°,∠CEB=90°,∴BE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com )BD= ( http: / / www.21cnjy.com ).在直角三角形ABC中,∠A=30°,则AB=2BC=2.则AE=AB﹣BE= ( http: / / www.21cnjy.com ).∵Rt△AEC≌Rt△DFC,∴DF=AE= ( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com )
26.解答: (1)证明:在△ABC和△ADC中, ( http: / / www.21cnjy.com ),∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,在△ABF和△ADF中, ( http: / / www.21cnjy.com ),∴△ABF≌△ADF(SAS),∴∠AFD=∠AFB,∵∠AFB=∠CFE,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD,又∵∠BAC=∠DAC,∴∠CAD=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当EB⊥CD时,∠EFD=∠BCD,理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF,在△BCF和△DCF中, ( http: / / www.21cnjy.com ),∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠EFD=∠BCD. ( http: / / www.21cnjy.com )
(考试时间90分钟)
一.选择题(共14小题,每小题3分)
1.由于受H7N9禽流感的影响,今年4月 ( http: / / www.21cnjy.com )份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤5元,下列所列方程中正确的是( )
A. 12(1+a%)2=5 B. 12(1﹣a%)2=5 C. 12(1﹣2a%)=5 D. 12(1﹣a2%)=5
2.将代数式x2+6x+2化成(x+p)2+q的形式为( )
A. (x﹣3)2+11 B. (x+3)2﹣7 C. (x+3)2﹣11 D. (x+2)2+4
3.一元二次方程x2+2x+2=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 只有一个实数根 D. 无实数根
4.三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )
A. 14 B. 12 C. 12或14 D. 以上都不对
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
5题图 6题图 7题图 8题图
5.如图,是用4个相同的小矩形与1个小正方 ( http: / / www.21cnjy.com )形镶嵌而成的正方形图案,已知该图案的面积为49,小正方形的面积为4,若用x,y表示小矩形的两边长(x>y),请观察图案,指出以下关系式中不正确的是( )
A. x+y=7 B. x﹣y=2 C. x2+y2=25 D. 4xy+4=49
6.如图,在△ABC中,∠ABC和∠ACB ( http: / / www.21cnjy.com )的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
A. 6 B. 7 C. 8 D. 9
7.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A. 50 B. 62 C. 65 D. 68
8.如图,过边长为3的等边 ( http: / / www.21cnjy.com )△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交边AC于点D,则DE的长为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. 不能确定
9.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( )
A. 6 B. 4 C. 3 D. 2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
9题图 11题图 12题图 14题图
10.下列说法中错误的是( )
A. 平行四边形的对角线互相平分
B. 有两对邻角互补的四边形为平行四边形
C. 对角线互相平分的四边形是平行四边形
D. 一组对边平行,一组对角相等的四边形是平行四边形
11.如图,等腰梯形ABCD中,AD∥BC,AB=DC,AD=3,AB=4,∠B=60°,则梯形的面积是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
12.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A. 100° B. 105° C. 110° D. 120°
13.下列各组条件中,能判定四边形ABCD为矩形的是( )
A. ∠A+∠B=90° B. AB∥CD,AB=CD,AC=BD
C. AB∥CD,AD=BC,AC=BD D. AC=BD,∠A=90°
14.如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是( )
A. b=a+c B. b=ac C. b2=a2+c2 D. b=2a=2c
二.填空题(共6小题,每小题3分)
15.若 ( http: / / www.21cnjy.com ),且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是_________.
16.已知x1、x2是方程2x2+14x﹣16=0的两实数根,那么 ( http: / / www.21cnjy.com )的值为 _________ .
17.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17题图 18题图 19题图
18.如图,在Rt△ABC中,∠C=9 ( http: / / www.21cnjy.com )0°,作AB的垂直平分线,交AB于D,交AC于E,连接BE.已知∠CBE=40°,则∠A= _________ 度.
19.如图,∠ABD、∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为 _________ .
20.关于x的方程mx2+3x=x2+4是一元二次方程,则m应满足条件是 _________ .
三.解答题(共6小题)
21.(每小题4分)
(1)用配方法解一元二次方程:3x2﹣6x﹣1=0;
(2)化简 ( http: / / www.21cnjy.com )
(3) ( http: / / www.21cnjy.com ) (4)2x2﹣7x+3=0.
22.(8分)己知a﹣b=4,(1)若ab+c2﹣2c+5=0,求b+c的值.
(2)若d2=ab+4,且d<b,求a+d的值.
23. (8分)如图,已知四边形A ( http: / / www.21cnjy.com )BCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.
( http: / / www.21cnjy.com )
24.(8分)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;(2)求证:四边形EBFD是平行四边形.
( http: / / www.21cnjy.com )
25.(8分)已知,如图,在Rt△ ( http: / / www.21cnjy.com )ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.(1)求证:GE=GF;(2)若BD=1,求DF的长.
( http: / / www.21cnjy.com )
26.(12分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.
( http: / / www.21cnjy.com )
2014年度大庆市房顶中学第二学期初三数学期中试卷
答案
一.选择题(共14小题)
1.B
2.B
3.D
4.B
5.C
6.D
7.A
8.B
9.B
10.B
11.A
12.A
13.B
14.A
二.填空题(共6小题)
15. k≤4且k≠0 .
16. ﹣ ( http: / / www.21cnjy.com ) .
17. ( http: / / www.21cnjy.com ) .
18. 25
19. 20° .
20. m≠1 .
三.解答题(共6小题)
21.(1)x1= ( http: / / www.21cnjy.com ),x2= ( http: / / www.21cnjy.com );
(2)x+1
(3)x1=﹣2+ ( http: / / www.21cnjy.com ),x2=﹣2﹣ ( http: / / www.21cnjy.com ),x3=0,x4=﹣2
(4)x1=3, ( http: / / www.21cnjy.com ).
22.(1)b+c=﹣1(2)a+d=2
23
( http: / / www.21cnjy.com )
24.解答: (1)证明:如图:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠3=∠4,∵∠1=∠3+∠5,∠2=∠4+∠6,∴∠1=∠2∴∠5=∠6∵在△ADE与△CBF中, ( http: / / www.21cnjy.com )∴△ADE≌△CBF(ASA),∴AE=CF;(2))证明:∵∠1=∠2,∴DE∥BF.又∵由(1)知△ADE≌△CBF,∴DE=BF,∴四边形EBFD是平行四边形. ( http: / / www.21cnjy.com )
25.解答: (1)证明:∵DF∥BC,∠ACB=90°,∴∠CFD=90°.∵CD⊥AB,∴∠AEC=90°.在Rt△AEC和Rt△DFC中,∠AEC=∠CFD=90°,∠ACE=∠DCF,DC=AC,∴Rt△AEC≌Rt△DFC.∴CE=CF.∴DE=AF.而∠AGF=∠DGE,∠AFG=∠DEG=90°,∴Rt△AFG≌Rt△DEG.∴GF=GE.(2)解:∵CD⊥AB,∠A=30°,∴CE= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com )CD.∴CE=ED.∴BC=BD=1.又∵∠ECB+∠ACE=90°,∠A+∠ACE=90°,∴∠ECB=∠A=30°,∠CEB=90°,∴BE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com )BD= ( http: / / www.21cnjy.com ).在直角三角形ABC中,∠A=30°,则AB=2BC=2.则AE=AB﹣BE= ( http: / / www.21cnjy.com ).∵Rt△AEC≌Rt△DFC,∴DF=AE= ( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com )
26.解答: (1)证明:在△ABC和△ADC中, ( http: / / www.21cnjy.com ),∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,在△ABF和△ADF中, ( http: / / www.21cnjy.com ),∴△ABF≌△ADF(SAS),∴∠AFD=∠AFB,∵∠AFB=∠CFE,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD,又∵∠BAC=∠DAC,∴∠CAD=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当EB⊥CD时,∠EFD=∠BCD,理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF,在△BCF和△DCF中, ( http: / / www.21cnjy.com ),∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠EFD=∠BCD. ( http: / / www.21cnjy.com )
同课章节目录
