第二十章 数据的分析单元测试卷(困难 含答案)
文档属性
| 名称 | 第二十章 数据的分析单元测试卷(困难 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 547.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-24 14:23:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册第二十章《数据的分析》单元测试卷(困难)(含答案解析)
考试范围:第二十章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1. 已知一组数据,,,的中位数与平均数相等,那么这组数据的中位数是( )
A. B. C. 或 D. 或
2. 有个正整数,平均数是,中位数是,唯一的众数是,则最大的正整数最大为( )
A. B. C. D.
3. 为参加全市中学生足球赛.某中学从全校学生中选拔名足球运动员组建校足球队,这名运动员的年龄岁如下表所示,该足球队队员的平均年龄是( )
年龄岁
人数
A. 岁 B. 岁 C. 岁 D. 岁
4. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:该班等及等以上占全班;等有人,没有得满分的按分制;成绩分数按分制的中位数在第三组;成绩分数按分制的众数在第三组,其中正确的是( )
A. B. C. D.
5. 一个民营企业名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )
人次
工资
A. 标准差 B. 平均数 C. 众数 D. 中位数
6. 关于七年级与班在运动会中的比赛成绩,甲同学说:班与班得分比为乙同学说:班得分是班得分的倍少分设班得分,班得分,则( )
A. B. C. D.
7. 下列说法正确的是( )
A. 为了了解一本书页的书稿中错别字的个数,应采用普查的调查方式进行;
B. 为了了解我市今年夏季冷饮市场冰激凌的质量可采用普查的调查方式进行;
C. 销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数;
D. 为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取份试卷进行统计分析,在这个问题中,样本是被抽取的名学生;
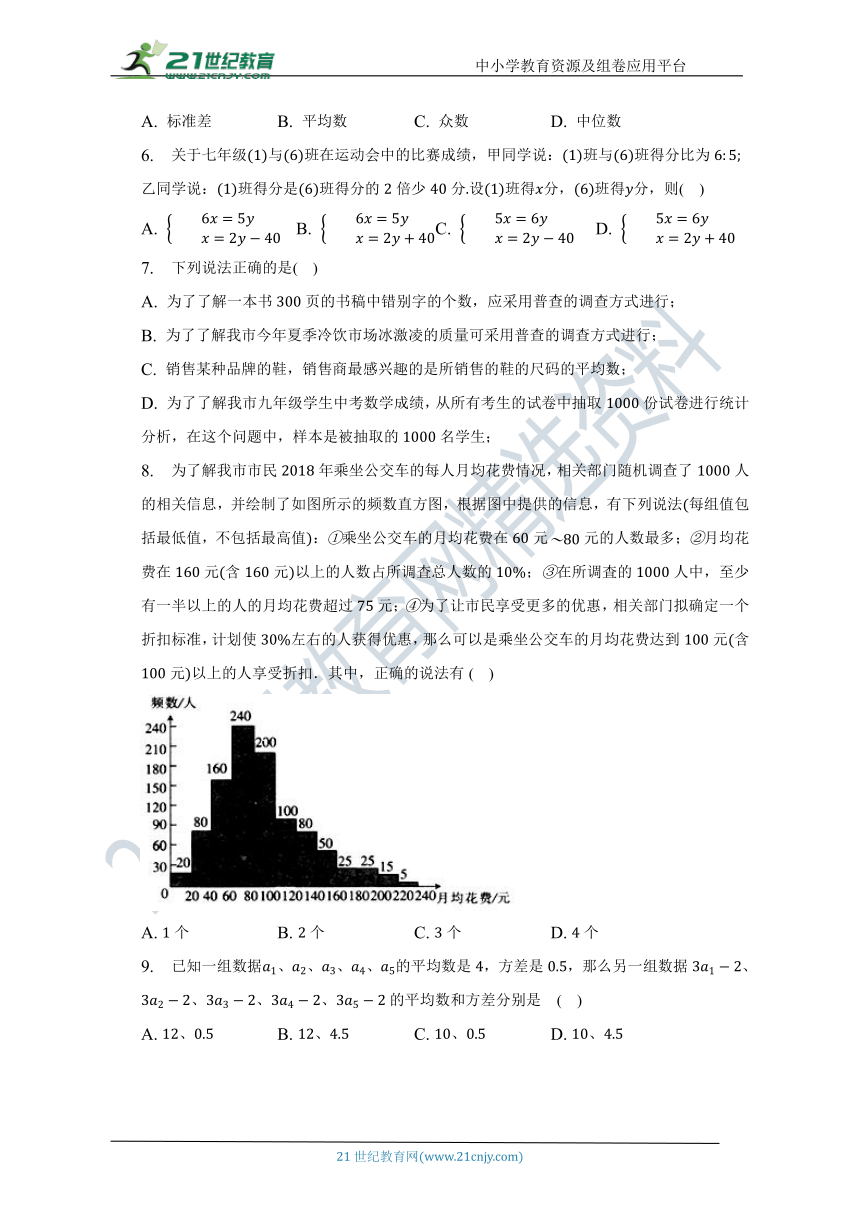
8. 为了解我市市民年乘坐公交车的每人月均花费情况,相关部门随机调查了人的相关信息,并绘制了如图所示的频数直方图,根据图中提供的信息,有下列说法每组值包括最低值,不包括最高值:乘坐公交车的月均花费在元元的人数最多;月均花费在元含元以上的人数占所调査总人数的;在所调査的人中,至少有一半以上的人的月均花费超过元;为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使左右的人获得优惠,那么可以是乘坐公交车的月均花费达到元含元以上的人享受折扣.其中,正确的说法有( )
A. 个 B. 个 C. 个 D. 个
9. 已知一组数据、、、、的平均数是,方差是,那么另一组数据、、、、的平均数和方差分别是 ( )
A. 、 B. 、 C. 、 D. 、
10. 已知一组数据,,,,的平均数是,方差是,那么另一组数据,,,,的平均数和方差分别是( )
A. , B. , C. , D. ,
11. 已知甲组数据,的方差 ,将甲组数据中每个数分别乘以后,再加得到乙组数据,则乙组数据的方差( )
A. B. C. D.
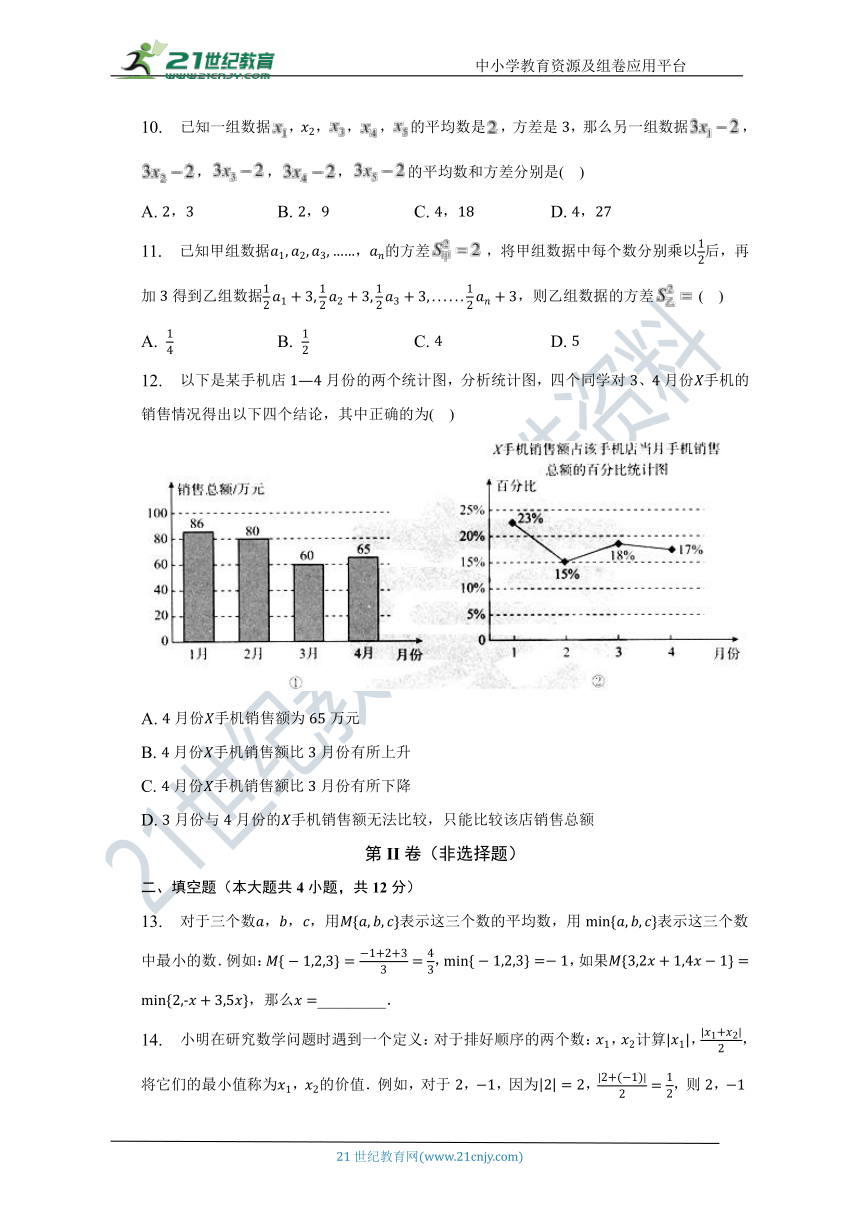
12. 以下是某手机店月份的两个统计图,分析统计图,四个同学对、月份手机的销售情况得出以下四个结论,其中正确的为( )
A. 月份手机销售额为万元
B. 月份手机销售额比月份有所上升
C. 月份手机销售额比月份有所下降
D. 月份与月份的手机销售额无法比较,只能比较该店销售总额
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13. 对于三个数,,,用表示这三个数的平均数,用表示这三个数中最小的数.例如:,,如果,那么_________.
14. 小明在研究数学问题时遇到一个定义:对于排好顺序的两个数:,计算,,将它们的最小值称为,的价值.例如,对于,,因为,,则,的价值为现将,这两个数按照不同的顺序排列,可得到这两个数价值的最小值为,则的值是 ______.
15. 已知一组数据,,,,的平均数是,方差是,那么另一组数据,,,,的平均数和方差的和为______.
16. 已知一组数据,,,的方差为,则另一组数据,,,的方差为________.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
为提高学生的安全防范意识,八年级组织了一场“安全伴着你我他”的知识竞赛活动,活动将成绩分为,,,四个等级,其中相应等级的得分依次记为分,分,分,分,成绩出来后,学校从中抽取了部分学生的成绩整理并绘制如下统计图,请你根据以上提供的信息解答下列问题:
在抽取的学生人数中成绩在级以上包括级的人数为______;
求这些学生成绩的平均数分、中位数分、众数分;
若八年级共有学生人,请估计一下,全校竞赛成绩等级是级的学生约有多少人?
18. 本小题分
附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集号电池节,号电池节,总重量为克;第二天收集号电池节,号电池节,总重量为克.
求号和号电池每节分别重多少克?
学校环保小组为估算四月份收集废电池的总重量,他们随意抽取了该月某天每天收集废电池的数量,如下表:
号电池单位:节
号电池单位:节
分别计算两种废电池的样本平均数;并由此估算该月天环保小组收集废电池的总重量是多少千克?
19. 本小题分
某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 阅读时间单位:小时 频数人数
图表中的______,______;
扇形统计图中组所对应的圆心角为______度;
该校共有学生名,请估计该校有多少名学生的每周平均课外阅读时间不低于小时?
20. 本小题分
某厂生产,两种产品,其单价需随市场变化而做相应调整.两种产品前三次单价变化的情况如下表所示:
第一次 第二次 第三次
产品单价元件
产品单价元件
产品第三次的单价比上一次的单价降低了___.
求两种产品三次单价的方差,并比较哪种产品的单价波动小.
该厂决定第四次调价,产品的单价仍为元件,产品的单价比元件上调,调整后产品这四次单价的中位数比产品这四次单价中位数的倍少,求的值.
21. 本小题分
在某旅游景区上山的一条小路上,有一些断断续续的台阶如图是其中的甲、乙两段台阶路的示意图请你用所学过的有关统计知识平均数、中位数、方差回答下列问题:
两段台阶路有哪些相同点和不同点
哪段台阶路走起来更舒服为什么
为方便游客行走,需要重新整修上山的小路对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
22. 本小题分
一次期中考试中,,,,,五位同学的数学、英语成绩有如下信息:
平均分 标准差
数学
英语
求这位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分个人成绩平均成绩成绩标准差.从标准分看,标准分高的考试成绩更好,请问同学在本次考试中,数学与英语哪个学科考得更好?
23. 本小题分
郴州市飞天山旅游景区上山的一条小路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶的示意图每级台阶旁的数字为该级台阶高度,单位为请你用所学过的有关统计知识平均数、中位数、方差等回答下列问题:
求甲段台阶高度的中位数和乙段台阶高度的众数;
试问甲、乙哪段台阶更方便游客行走?在台阶数量不变的情况下,如果要将不方便行走的该段台阶进行整修,请你提出合理的整修建议.
24. 本小题分
某校举办了一次成语知识竞赛,满分分,学生得分均为整数,成绩达到分及分以上为合格,达到分或分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
组别 平均分 中位数 方差 合格率 优秀率
甲组
乙组
直接写出下列成绩统计分析表中,,的值;
小英同学说:“这次竞赛我得了分,在我们小组中排名属中游略偏上”观察上面表格判断,小英是甲、乙哪个组的学生?
甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
25. 本小题分
阅读下列材料:
延庆是全市唯一一个全境域都是水源保护地的区域,森林覆盖率达到,“干净指数”连续五年全市第一,人均公共绿地面积平方米,空气质量长期保持全市前列.根据区环保局的空气质量的通报,年空气质量为优,成为北京市最宜居的地方.
由于经济发展,私家车剧增等原因,年空气质量下降为良,尤其是平均浓度有所增长,年平均浓度约为微克立方米,比年平均浓度增长了延庆区作为年世园会和年冬奥会比赛的举办地,将全面治理“煤、气、尘”,逐渐降低浓度,力争到年降至微克立方米,实现“延庆蓝”.
据悉,延庆将大力推广地源热泵、风能、太阳能等新能源和可再生能源.同时强化大货车监管,提升新能源车辆利用率.年新能源和可再生能源在延庆的使用比例将达到,煤炭能源消费总量占比以下,基本建成“无煤区”.
经过全面治理,年平均浓度约为微克立方米,比年平均浓度降低了;年平均浓度比年平均浓度降低了,为全市最低;年平均浓度约为微克立方米.
根据以上材料解答下列问题:
年平均浓度约为______微克立方米;
选择统计表或统计图,将年平均浓度整理出来;
根据上述材料和绘制的统计表或统计图中提供的信息,预估年的平均浓度约为______微克立方米;你的预估理由是______.
答案和解析
1.【答案】
【解析】
【分析】
本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数,因为中位数的值与大小排列顺序有关,而此题中的大小位置未定,故应该分类讨论所处的所有位置情况:从小到大或从大到小排列在中间在第二位或第三位结果不影响;结尾;开始的位置.
【解答】
解:将这组数据从大到小的顺序排列后,,,,处于中间位置的那个数是,,
那么由中位数的定义可知,,
,符合题意;中位数为:
将这组数据从大到小的顺序排列后,,,,中位数是,
此时平均数是,
,符合题意;
将这组数据从大到小的顺序排列后,,,,中位数是,
平均数,
,符合题意;
所以中位数是或.
故选D.
2.【答案】
【解析】
【分析】
本题主要考查了众数、平均数以及中位数的运用,解题时注意:一组数据中出现次数最多的数据叫做众数.将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.
根据个正整数,平均数是,中位数是,众数只有一个,经过推理验证即可得到个正整数为,,,,,,,,,,时满足题意.
【解答】
解:个正整数的平均数是,
这个数的和为.
设最大的正整数为,
这个数据的中位数是,众数只有一个,
如有两个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,.
这个数据的和,
比较上面各组数据中哪个更大即可,通过计算可知分别为,,,,故这组数据中最大的正整数最大为.
故选:.
3.【答案】
【解析】解:该足球队队员的平均年龄是岁,
故选:.
直接利用加权平均数的定义计算可得.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
4.【答案】
【解析】
【分析】
本题考查的是众数,中位数有关知识,根据百分比,中位数,众数的定义对每个问题分别解答,即可确定选项.
【解答】
解:,正确,
等有人,但看不出其具体的份数,错误,
该班共有人,在等,等的义工人,所以中位数在第三组,正确,
虽然第三组的人数多,但成绩分数不确定,所以众数不确定,错误.
故选C.
5.【答案】
【解析】
【分析】
此题主要考查了平均数以及中位数和众数的定义求法和标准差的意义,正确把握相关定义是解题关键.分别利用平均数以及中位数和众数的定义求法和标准差的意义分别分析得出答案.
【解答】
解:平均数为:,
中位数是:,
众数是:,
标准差反映的是数据的波动大小,无法反映这些员工月平均工资水平,只有中位数,能够较好反映这些员工月平均工资水平.
故选D.
6.【答案】
【解析】
【分析】
此题主要考查了二元一次方程组的应用.
设班得分,班得分,根据:班与班得分比为:;班得分比班得分的倍少分即可列出方程组.
【解答】
解:设班得分,班得分,
根据题意可得:,
故选C.
7.【答案】
【解析】
【分析】
此题主要考查了全面调查和抽样调查,正确把握相关定义是解题关键,直接利用全面调查与抽样调查的意义分析得出答案.
【解答】
解:为了了解一本书页的书稿中错别字的个数,应采用普查的调查方式进行,此选项正确;
B.为了了解我市今年夏季冷饮市场冰激凌的质量可采用抽样的调查方式进行,此选项错误;
C.销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的众数,此选项错误;
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取份试卷进行统计分析,在这个问题中,样本是被抽取的名学生的成绩,此选项错误;
故选A.
8.【答案】
【解析】
【分析】
本题主要考查了频数分布直方图,平均数以及中位数的应用,将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,根据频数分布直方图中的数据,求得众数,平均数,中位数,即可得出结论.
【解答】
解:根据频数分布直方图,可得众数为元范围,故乘坐公交车的月均花费在元元的人数最多,故正确;
根据频数分布直方图,可得月均花费在元含元以上的人数占所调査总人数的,故错误;
根据频数分布直方图,可得在所调査的人中,至少有一半以上的人的月均花费超过元,故正确;
根据频数分布直方图,可得为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使左右的人获得优惠,那么可以是乘坐公交车的月均花费达到元含元以上的人享受折扣,故正确.
故选C.
9.【答案】
【解析】
【分析】
本题考查了方差和平均数:关键是掌握方差和平均数的变化规律,根据方差和平均数的变化规律可得:数据,,,,的平均数是,方差是,再进行计算即可.
【解答】
解:数据,,,,的平均数是,
另一组数据,,,,的平均数是;
数据,,,,的方差是,
另一组数据,,,,的方差是,
另一组数据,,,,的方差是.
故选D.
10.【答案】
【解析】
【分析】
本题考查了方差的知识,说明了当数据都加上一个数或减去一个数时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍.根据数据的变化和其平均数及方差的变化规律求得新数据的平均数及方差即可.
【解答】
解:当一组数据中的每一个数据发生什么样的变化其平均数就发生什么样的变化,
,,,,的平均数数据,,,,的平均数的倍减,
数据,,,,的平均数是,
,,,,的平均数为:,
当一组数据同时加上一个常数不影响方差,
乘以一个常数则其方差变为原来的常数的平方倍,
,,,,的方差为:.
故选D.
11.【答案】
【解析】
【分析】
本题考查了当数据都乘以一个数时,方差变为原来的倍,是基础题目,方差是用来衡量一组数据波动大小的量,每个数都乘以,所以平均数变,方差也变,加一个数之后,平均数变化,方差没变.
【解答】
解:由题意知,甲数据为,,,
设甲的平均数为,乙的平均数为
,
故选B.
12.【答案】
【解析】
【分析】
A.月份手机销售总额为万元,并非是三星手机销售额为万元,故A选项错误
B.月份三星手机销售额为万元,月份三星手机销售额为万元,所以月份三星手机销售额大于月份三星手机销售额,故 B选项正确
C.由分析可知:月份三星手机销售额比月份有所下降判断错误,应是有所上升
D.由分析可知:月份与月份的三星手机销售额可以比较,故D选项错误
故选B.
【解答】月份手机的销售额是万元,月份手机的销售额是万元故月份手机销售额比月份有所上升.
故选B.
13.【答案】或
【解析】
【分析】
本题考查了一元一次方程的解法、平均数及新定义运算,解决的关键是读懂题意,据题意结合方程和新定义规则求解,根据表示这三个数的平均数,先求出的值,然后根据,即可求出的取值范围.
【解答】
解:,
,
有如下三种情况:
,,此时,成立;
,,此时,不成立;
,,此时,成立,
或,
故答案为或.
14.【答案】或或或.
【解析】
【分析】
本题考查的是算术平均数的有关知识,由题意利用给出的新定义,建立关于的方程进行求解即可.
【解答】
解:由题意可得:
当时,
解得:或.
当时,
解得:或.
故答案为或或或.
15.【答案】
【解析】解:数据,,,,的平均数是,
数据,,,,的平均数是;
数据,,,,的方差为,
数据,,,,的方差是,
数据,,,,的方差是;
数据,,,,的平均数和方差的和为:.
故答案为:.
根据平均数的变化规律可得出数据,,,,的平均数是;先根据数据,,,,的方差为,求出数据,,,,的方差是,即可得出数据,,,,的平均数和方差的和.
此题考查了平均数和方差,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.【答案】
【解析】
【分析】
本题主要考查了方差,先设这组数据,,,的平均数为,则另一组新数据,,,的平均数为,然后运用方差公式,根据由方差计算即可.
【解答】
解:设这组数据,,,的平均数为,
,
.
故答案为.
17.【答案】
【解析】解:由统计图知级以上包括级的人数为人;
平均分为分;
竞赛成绩是级的学生约有人.
直接从条形统计图中看出成绩在级以上包括级的人数为人;
用加权平均数计算平均分,利用中位数及众数的定义求得这两个量即可;
首先求得成绩为级的人数占被抽查的人数的百分比,然后用样本估计总体即可;
本题考查了条形统计图及用样本估计总体的知识,解题的关键是仔细读图并从条形统计图中整理出进一步解题的有关信息.
18.【答案】解:设号电池每节重克,号电池每节重克,
根据题意得
解之得.
节;节
总重量千克.
答:号和号电池每节分别重克,克;
两种废电池的样本平均数分别为节,节.该月天环保小组收集废电池的总重量是千克.
【解析】根据题意列出方程组求出号电池和号电池的重量,然后再利用平均数求出电池的总重量.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.学会用样本估计总体的方法也是解决此题的关键.
19.【答案】
【解析】解:,;
扇形统计图中组所对应的圆心角为:;
由题意得,每周平均课外阅读时间不低于小时的学生数为:名.
故答案为:,,.
根据题意列式计算即可;
组所对应的百分数即可得到结论;
根据题意列式计算即可得到结论.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
20.【答案】解:;
,
,
产品的方差小,
产品的单价波动小;
第四次调价后,对于产品,这四次单价的中位数为;
对于产品,,
第四次单价大于,
,
第四次单价小于,
,
.
【解析】
【分析】
本题考查了方差,算术平均数,中位数的知识,解题的关键是根据方差公式进行有关的运算,难度不大.
根据题目提供数据计算即可;
分别计算平均数及方差即可;用第二次的单价减去第三次的单价除以第二次的单价计算即可;
首先确定这四次单价的中位数,然后确定第四次调价的范围,根据“产品这四次单价的中位数是产品四次单价中位数的倍少”列式求即可.
【解答】
解:产品第三次的单价比上一次的单价降低了;
故答案为;
见答案;
见答案.
21.【答案】解:
因为,
甲路段的中位数为,乙路段的中位数为
,,
所以相同点:两段台阶路每一级台阶高度的平均数相同
不同点:两段台阶路每一级台阶高度的中位数、方差不同.
甲段台阶路走起来更舒服,因为它的每一级台阶高度的方差小.
每一级台阶高度均整修为原每一级台阶高度的平均数,使得方差为,此时游客行走最方便.
【解析】略
22.【答案】解:数学平均分是:分,
英语标准差为:;
数学标准分,英语标准分,,
数学更好.
【解析】由平均数、标准差的公式进行计算即可;
代入公式:标准分个人成绩平均成绩成绩标准差计算,再比较即可.
本题考查的是标准差的计算,计算标准差需要先算出方差,计算方差的步骤是:计算数据的平均数;计算偏差,即每个数据与平均数的差;计算偏差的平方和;偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.
23.【答案】解:甲段台阶高度的中位数是,乙段台阶高度的众数是;
乙段台阶更方便游客行走,
因为甲路段台阶高度的平均数是,
所以按每级台阶为的高度进行整修.
【解析】根据中位数和和众数的定义即可求解;
由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
此题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
24.【答案】解:甲组:分的有人,分有人,分的有人,分的有人,分的有人,
乙组:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,
,,;
甲:分的有人,分有人,分的有人,分的有人,分的有人,
乙:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,
小英是甲组的学生;
支持乙组同学观点的理由是乙组的平均分高于甲组,乙组的方差小,比甲组稳定.
【解析】先根据图形得出甲组:分的有人,分有人,分的有人,分的有人,分的有人;乙组:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,再分别求出即可;
根据图中数据得出即可;
从平均数和方差得出即可.
本题考查了折线统计图,中位数和方差等知识点,能正确根据折线统计图得出正确信息是解此题的关键.
25.【答案】 近三年平均浓度平均每年降低约微克立方米
【解析】解:年平均浓度比年平均浓度降低了,
年平均浓度约为微克立方米,
故答案为:;
年平均浓度如下表所示,
根据近三年平均浓度平均每年降低微克立方米,
可得年的平均浓度约为微克立方米.
故答案为:,近三年平均浓度平均每年降低约微克立方米.
根据年平均浓度比年平均浓度降低了,进行计算即可;
根据年平均浓度的值,画统计表即可;
根据近三年平均浓度平均每年降低微克立方米,可得年的平均浓度.
本题主要考查了统计图的选择以及用样本估计总体的运用,解题时注意:根据具体问题选择合适的统计图,可以使数据变得清晰直观.
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册第二十章《数据的分析》单元测试卷(困难)(含答案解析)
考试范围:第二十章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1. 已知一组数据,,,的中位数与平均数相等,那么这组数据的中位数是( )
A. B. C. 或 D. 或
2. 有个正整数,平均数是,中位数是,唯一的众数是,则最大的正整数最大为( )
A. B. C. D.
3. 为参加全市中学生足球赛.某中学从全校学生中选拔名足球运动员组建校足球队,这名运动员的年龄岁如下表所示,该足球队队员的平均年龄是( )
年龄岁
人数
A. 岁 B. 岁 C. 岁 D. 岁
4. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:该班等及等以上占全班;等有人,没有得满分的按分制;成绩分数按分制的中位数在第三组;成绩分数按分制的众数在第三组,其中正确的是( )
A. B. C. D.
5. 一个民营企业名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )
人次
工资
A. 标准差 B. 平均数 C. 众数 D. 中位数
6. 关于七年级与班在运动会中的比赛成绩,甲同学说:班与班得分比为乙同学说:班得分是班得分的倍少分设班得分,班得分,则( )
A. B. C. D.
7. 下列说法正确的是( )
A. 为了了解一本书页的书稿中错别字的个数,应采用普查的调查方式进行;
B. 为了了解我市今年夏季冷饮市场冰激凌的质量可采用普查的调查方式进行;
C. 销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数;
D. 为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取份试卷进行统计分析,在这个问题中,样本是被抽取的名学生;
8. 为了解我市市民年乘坐公交车的每人月均花费情况,相关部门随机调查了人的相关信息,并绘制了如图所示的频数直方图,根据图中提供的信息,有下列说法每组值包括最低值,不包括最高值:乘坐公交车的月均花费在元元的人数最多;月均花费在元含元以上的人数占所调査总人数的;在所调査的人中,至少有一半以上的人的月均花费超过元;为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使左右的人获得优惠,那么可以是乘坐公交车的月均花费达到元含元以上的人享受折扣.其中,正确的说法有( )
A. 个 B. 个 C. 个 D. 个
9. 已知一组数据、、、、的平均数是,方差是,那么另一组数据、、、、的平均数和方差分别是 ( )
A. 、 B. 、 C. 、 D. 、
10. 已知一组数据,,,,的平均数是,方差是,那么另一组数据,,,,的平均数和方差分别是( )
A. , B. , C. , D. ,
11. 已知甲组数据,的方差 ,将甲组数据中每个数分别乘以后,再加得到乙组数据,则乙组数据的方差( )
A. B. C. D.
12. 以下是某手机店月份的两个统计图,分析统计图,四个同学对、月份手机的销售情况得出以下四个结论,其中正确的为( )
A. 月份手机销售额为万元
B. 月份手机销售额比月份有所上升
C. 月份手机销售额比月份有所下降
D. 月份与月份的手机销售额无法比较,只能比较该店销售总额
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13. 对于三个数,,,用表示这三个数的平均数,用表示这三个数中最小的数.例如:,,如果,那么_________.
14. 小明在研究数学问题时遇到一个定义:对于排好顺序的两个数:,计算,,将它们的最小值称为,的价值.例如,对于,,因为,,则,的价值为现将,这两个数按照不同的顺序排列,可得到这两个数价值的最小值为,则的值是 ______.
15. 已知一组数据,,,,的平均数是,方差是,那么另一组数据,,,,的平均数和方差的和为______.
16. 已知一组数据,,,的方差为,则另一组数据,,,的方差为________.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
为提高学生的安全防范意识,八年级组织了一场“安全伴着你我他”的知识竞赛活动,活动将成绩分为,,,四个等级,其中相应等级的得分依次记为分,分,分,分,成绩出来后,学校从中抽取了部分学生的成绩整理并绘制如下统计图,请你根据以上提供的信息解答下列问题:
在抽取的学生人数中成绩在级以上包括级的人数为______;
求这些学生成绩的平均数分、中位数分、众数分;
若八年级共有学生人,请估计一下,全校竞赛成绩等级是级的学生约有多少人?
18. 本小题分
附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集号电池节,号电池节,总重量为克;第二天收集号电池节,号电池节,总重量为克.
求号和号电池每节分别重多少克?
学校环保小组为估算四月份收集废电池的总重量,他们随意抽取了该月某天每天收集废电池的数量,如下表:
号电池单位:节
号电池单位:节
分别计算两种废电池的样本平均数;并由此估算该月天环保小组收集废电池的总重量是多少千克?
19. 本小题分
某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 阅读时间单位:小时 频数人数
图表中的______,______;
扇形统计图中组所对应的圆心角为______度;
该校共有学生名,请估计该校有多少名学生的每周平均课外阅读时间不低于小时?
20. 本小题分
某厂生产,两种产品,其单价需随市场变化而做相应调整.两种产品前三次单价变化的情况如下表所示:
第一次 第二次 第三次
产品单价元件
产品单价元件
产品第三次的单价比上一次的单价降低了___.
求两种产品三次单价的方差,并比较哪种产品的单价波动小.
该厂决定第四次调价,产品的单价仍为元件,产品的单价比元件上调,调整后产品这四次单价的中位数比产品这四次单价中位数的倍少,求的值.
21. 本小题分
在某旅游景区上山的一条小路上,有一些断断续续的台阶如图是其中的甲、乙两段台阶路的示意图请你用所学过的有关统计知识平均数、中位数、方差回答下列问题:
两段台阶路有哪些相同点和不同点
哪段台阶路走起来更舒服为什么
为方便游客行走,需要重新整修上山的小路对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
22. 本小题分
一次期中考试中,,,,,五位同学的数学、英语成绩有如下信息:
平均分 标准差
数学
英语
求这位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分个人成绩平均成绩成绩标准差.从标准分看,标准分高的考试成绩更好,请问同学在本次考试中,数学与英语哪个学科考得更好?
23. 本小题分
郴州市飞天山旅游景区上山的一条小路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶的示意图每级台阶旁的数字为该级台阶高度,单位为请你用所学过的有关统计知识平均数、中位数、方差等回答下列问题:
求甲段台阶高度的中位数和乙段台阶高度的众数;
试问甲、乙哪段台阶更方便游客行走?在台阶数量不变的情况下,如果要将不方便行走的该段台阶进行整修,请你提出合理的整修建议.
24. 本小题分
某校举办了一次成语知识竞赛,满分分,学生得分均为整数,成绩达到分及分以上为合格,达到分或分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
组别 平均分 中位数 方差 合格率 优秀率
甲组
乙组
直接写出下列成绩统计分析表中,,的值;
小英同学说:“这次竞赛我得了分,在我们小组中排名属中游略偏上”观察上面表格判断,小英是甲、乙哪个组的学生?
甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
25. 本小题分
阅读下列材料:
延庆是全市唯一一个全境域都是水源保护地的区域,森林覆盖率达到,“干净指数”连续五年全市第一,人均公共绿地面积平方米,空气质量长期保持全市前列.根据区环保局的空气质量的通报,年空气质量为优,成为北京市最宜居的地方.
由于经济发展,私家车剧增等原因,年空气质量下降为良,尤其是平均浓度有所增长,年平均浓度约为微克立方米,比年平均浓度增长了延庆区作为年世园会和年冬奥会比赛的举办地,将全面治理“煤、气、尘”,逐渐降低浓度,力争到年降至微克立方米,实现“延庆蓝”.
据悉,延庆将大力推广地源热泵、风能、太阳能等新能源和可再生能源.同时强化大货车监管,提升新能源车辆利用率.年新能源和可再生能源在延庆的使用比例将达到,煤炭能源消费总量占比以下,基本建成“无煤区”.
经过全面治理,年平均浓度约为微克立方米,比年平均浓度降低了;年平均浓度比年平均浓度降低了,为全市最低;年平均浓度约为微克立方米.
根据以上材料解答下列问题:
年平均浓度约为______微克立方米;
选择统计表或统计图,将年平均浓度整理出来;
根据上述材料和绘制的统计表或统计图中提供的信息,预估年的平均浓度约为______微克立方米;你的预估理由是______.
答案和解析
1.【答案】
【解析】
【分析】
本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数,因为中位数的值与大小排列顺序有关,而此题中的大小位置未定,故应该分类讨论所处的所有位置情况:从小到大或从大到小排列在中间在第二位或第三位结果不影响;结尾;开始的位置.
【解答】
解:将这组数据从大到小的顺序排列后,,,,处于中间位置的那个数是,,
那么由中位数的定义可知,,
,符合题意;中位数为:
将这组数据从大到小的顺序排列后,,,,中位数是,
此时平均数是,
,符合题意;
将这组数据从大到小的顺序排列后,,,,中位数是,
平均数,
,符合题意;
所以中位数是或.
故选D.
2.【答案】
【解析】
【分析】
本题主要考查了众数、平均数以及中位数的运用,解题时注意:一组数据中出现次数最多的数据叫做众数.将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.
根据个正整数,平均数是,中位数是,众数只有一个,经过推理验证即可得到个正整数为,,,,,,,,,,时满足题意.
【解答】
解:个正整数的平均数是,
这个数的和为.
设最大的正整数为,
这个数据的中位数是,众数只有一个,
如有两个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,
如有个,则其他数至多个,符合条件的数据可以是,,,,,,,,,,.
这个数据的和,
比较上面各组数据中哪个更大即可,通过计算可知分别为,,,,故这组数据中最大的正整数最大为.
故选:.
3.【答案】
【解析】解:该足球队队员的平均年龄是岁,
故选:.
直接利用加权平均数的定义计算可得.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
4.【答案】
【解析】
【分析】
本题考查的是众数,中位数有关知识,根据百分比,中位数,众数的定义对每个问题分别解答,即可确定选项.
【解答】
解:,正确,
等有人,但看不出其具体的份数,错误,
该班共有人,在等,等的义工人,所以中位数在第三组,正确,
虽然第三组的人数多,但成绩分数不确定,所以众数不确定,错误.
故选C.
5.【答案】
【解析】
【分析】
此题主要考查了平均数以及中位数和众数的定义求法和标准差的意义,正确把握相关定义是解题关键.分别利用平均数以及中位数和众数的定义求法和标准差的意义分别分析得出答案.
【解答】
解:平均数为:,
中位数是:,
众数是:,
标准差反映的是数据的波动大小,无法反映这些员工月平均工资水平,只有中位数,能够较好反映这些员工月平均工资水平.
故选D.
6.【答案】
【解析】
【分析】
此题主要考查了二元一次方程组的应用.
设班得分,班得分,根据:班与班得分比为:;班得分比班得分的倍少分即可列出方程组.
【解答】
解:设班得分,班得分,
根据题意可得:,
故选C.
7.【答案】
【解析】
【分析】
此题主要考查了全面调查和抽样调查,正确把握相关定义是解题关键,直接利用全面调查与抽样调查的意义分析得出答案.
【解答】
解:为了了解一本书页的书稿中错别字的个数,应采用普查的调查方式进行,此选项正确;
B.为了了解我市今年夏季冷饮市场冰激凌的质量可采用抽样的调查方式进行,此选项错误;
C.销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的众数,此选项错误;
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取份试卷进行统计分析,在这个问题中,样本是被抽取的名学生的成绩,此选项错误;
故选A.
8.【答案】
【解析】
【分析】
本题主要考查了频数分布直方图,平均数以及中位数的应用,将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,根据频数分布直方图中的数据,求得众数,平均数,中位数,即可得出结论.
【解答】
解:根据频数分布直方图,可得众数为元范围,故乘坐公交车的月均花费在元元的人数最多,故正确;
根据频数分布直方图,可得月均花费在元含元以上的人数占所调査总人数的,故错误;
根据频数分布直方图,可得在所调査的人中,至少有一半以上的人的月均花费超过元,故正确;
根据频数分布直方图,可得为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使左右的人获得优惠,那么可以是乘坐公交车的月均花费达到元含元以上的人享受折扣,故正确.
故选C.
9.【答案】
【解析】
【分析】
本题考查了方差和平均数:关键是掌握方差和平均数的变化规律,根据方差和平均数的变化规律可得:数据,,,,的平均数是,方差是,再进行计算即可.
【解答】
解:数据,,,,的平均数是,
另一组数据,,,,的平均数是;
数据,,,,的方差是,
另一组数据,,,,的方差是,
另一组数据,,,,的方差是.
故选D.
10.【答案】
【解析】
【分析】
本题考查了方差的知识,说明了当数据都加上一个数或减去一个数时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍.根据数据的变化和其平均数及方差的变化规律求得新数据的平均数及方差即可.
【解答】
解:当一组数据中的每一个数据发生什么样的变化其平均数就发生什么样的变化,
,,,,的平均数数据,,,,的平均数的倍减,
数据,,,,的平均数是,
,,,,的平均数为:,
当一组数据同时加上一个常数不影响方差,
乘以一个常数则其方差变为原来的常数的平方倍,
,,,,的方差为:.
故选D.
11.【答案】
【解析】
【分析】
本题考查了当数据都乘以一个数时,方差变为原来的倍,是基础题目,方差是用来衡量一组数据波动大小的量,每个数都乘以,所以平均数变,方差也变,加一个数之后,平均数变化,方差没变.
【解答】
解:由题意知,甲数据为,,,
设甲的平均数为,乙的平均数为
,
故选B.
12.【答案】
【解析】
【分析】
A.月份手机销售总额为万元,并非是三星手机销售额为万元,故A选项错误
B.月份三星手机销售额为万元,月份三星手机销售额为万元,所以月份三星手机销售额大于月份三星手机销售额,故 B选项正确
C.由分析可知:月份三星手机销售额比月份有所下降判断错误,应是有所上升
D.由分析可知:月份与月份的三星手机销售额可以比较,故D选项错误
故选B.
【解答】月份手机的销售额是万元,月份手机的销售额是万元故月份手机销售额比月份有所上升.
故选B.
13.【答案】或
【解析】
【分析】
本题考查了一元一次方程的解法、平均数及新定义运算,解决的关键是读懂题意,据题意结合方程和新定义规则求解,根据表示这三个数的平均数,先求出的值,然后根据,即可求出的取值范围.
【解答】
解:,
,
有如下三种情况:
,,此时,成立;
,,此时,不成立;
,,此时,成立,
或,
故答案为或.
14.【答案】或或或.
【解析】
【分析】
本题考查的是算术平均数的有关知识,由题意利用给出的新定义,建立关于的方程进行求解即可.
【解答】
解:由题意可得:
当时,
解得:或.
当时,
解得:或.
故答案为或或或.
15.【答案】
【解析】解:数据,,,,的平均数是,
数据,,,,的平均数是;
数据,,,,的方差为,
数据,,,,的方差是,
数据,,,,的方差是;
数据,,,,的平均数和方差的和为:.
故答案为:.
根据平均数的变化规律可得出数据,,,,的平均数是;先根据数据,,,,的方差为,求出数据,,,,的方差是,即可得出数据,,,,的平均数和方差的和.
此题考查了平均数和方差,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.【答案】
【解析】
【分析】
本题主要考查了方差,先设这组数据,,,的平均数为,则另一组新数据,,,的平均数为,然后运用方差公式,根据由方差计算即可.
【解答】
解:设这组数据,,,的平均数为,
,
.
故答案为.
17.【答案】
【解析】解:由统计图知级以上包括级的人数为人;
平均分为分;
竞赛成绩是级的学生约有人.
直接从条形统计图中看出成绩在级以上包括级的人数为人;
用加权平均数计算平均分,利用中位数及众数的定义求得这两个量即可;
首先求得成绩为级的人数占被抽查的人数的百分比,然后用样本估计总体即可;
本题考查了条形统计图及用样本估计总体的知识,解题的关键是仔细读图并从条形统计图中整理出进一步解题的有关信息.
18.【答案】解:设号电池每节重克,号电池每节重克,
根据题意得
解之得.
节;节
总重量千克.
答:号和号电池每节分别重克,克;
两种废电池的样本平均数分别为节,节.该月天环保小组收集废电池的总重量是千克.
【解析】根据题意列出方程组求出号电池和号电池的重量,然后再利用平均数求出电池的总重量.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.学会用样本估计总体的方法也是解决此题的关键.
19.【答案】
【解析】解:,;
扇形统计图中组所对应的圆心角为:;
由题意得,每周平均课外阅读时间不低于小时的学生数为:名.
故答案为:,,.
根据题意列式计算即可;
组所对应的百分数即可得到结论;
根据题意列式计算即可得到结论.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
20.【答案】解:;
,
,
产品的方差小,
产品的单价波动小;
第四次调价后,对于产品,这四次单价的中位数为;
对于产品,,
第四次单价大于,
,
第四次单价小于,
,
.
【解析】
【分析】
本题考查了方差,算术平均数,中位数的知识,解题的关键是根据方差公式进行有关的运算,难度不大.
根据题目提供数据计算即可;
分别计算平均数及方差即可;用第二次的单价减去第三次的单价除以第二次的单价计算即可;
首先确定这四次单价的中位数,然后确定第四次调价的范围,根据“产品这四次单价的中位数是产品四次单价中位数的倍少”列式求即可.
【解答】
解:产品第三次的单价比上一次的单价降低了;
故答案为;
见答案;
见答案.
21.【答案】解:
因为,
甲路段的中位数为,乙路段的中位数为
,,
所以相同点:两段台阶路每一级台阶高度的平均数相同
不同点:两段台阶路每一级台阶高度的中位数、方差不同.
甲段台阶路走起来更舒服,因为它的每一级台阶高度的方差小.
每一级台阶高度均整修为原每一级台阶高度的平均数,使得方差为,此时游客行走最方便.
【解析】略
22.【答案】解:数学平均分是:分,
英语标准差为:;
数学标准分,英语标准分,,
数学更好.
【解析】由平均数、标准差的公式进行计算即可;
代入公式:标准分个人成绩平均成绩成绩标准差计算,再比较即可.
本题考查的是标准差的计算,计算标准差需要先算出方差,计算方差的步骤是:计算数据的平均数;计算偏差,即每个数据与平均数的差;计算偏差的平方和;偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.
23.【答案】解:甲段台阶高度的中位数是,乙段台阶高度的众数是;
乙段台阶更方便游客行走,
因为甲路段台阶高度的平均数是,
所以按每级台阶为的高度进行整修.
【解析】根据中位数和和众数的定义即可求解;
由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
此题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
24.【答案】解:甲组:分的有人,分有人,分的有人,分的有人,分的有人,
乙组:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,
,,;
甲:分的有人,分有人,分的有人,分的有人,分的有人,
乙:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,
小英是甲组的学生;
支持乙组同学观点的理由是乙组的平均分高于甲组,乙组的方差小,比甲组稳定.
【解析】先根据图形得出甲组:分的有人,分有人,分的有人,分的有人,分的有人;乙组:分的有人,分有人,分的有人,分的有人,分的有人,分的有人,再分别求出即可;
根据图中数据得出即可;
从平均数和方差得出即可.
本题考查了折线统计图,中位数和方差等知识点,能正确根据折线统计图得出正确信息是解此题的关键.
25.【答案】 近三年平均浓度平均每年降低约微克立方米
【解析】解:年平均浓度比年平均浓度降低了,
年平均浓度约为微克立方米,
故答案为:;
年平均浓度如下表所示,
根据近三年平均浓度平均每年降低微克立方米,
可得年的平均浓度约为微克立方米.
故答案为:,近三年平均浓度平均每年降低约微克立方米.
根据年平均浓度比年平均浓度降低了,进行计算即可;
根据年平均浓度的值,画统计表即可;
根据近三年平均浓度平均每年降低微克立方米,可得年的平均浓度.
本题主要考查了统计图的选择以及用样本估计总体的运用,解题时注意:根据具体问题选择合适的统计图,可以使数据变得清晰直观.
21世纪教育网(www.21cnjy.com)
