19.2.2 第4课时 一次函数的实际应用 人教版八年级数学下册 教学课件(共19张PPT)
文档属性
| 名称 | 19.2.2 第4课时 一次函数的实际应用 人教版八年级数学下册 教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
19.2 一次函数
19.2.2 一次函数
第十九章 一次函数
课程讲授
新知导入
随堂练习
课堂小结
第4课时 一次函数的实际应用
知识要点
1.一次函数的简单应用
2.分段函数的应用
新知导入
看一看:
利用函数方法解决实际问题,关键是分析题中的
数量关系,联系实际生活及以前学过的内容,将
实际问题抽象、升华为一次函数模型,即建模,
再利用函数的性质解决问题.一次函数的应用主
要有两种类型:
新知导入
看一看:
(1)给出了一次函数关系式,直接应用一次函数
的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数
的情境时,应先求出关系式,进而利用函数
性质解决问题.
例 某弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如图所示,当所挂物体质量为20 kg时,弹簧的长度为( )
A. 20 cm
B. 25 cm
C. 30 cm
D.无法确定
课程讲授
1
一次函数的简单应用
A
课程讲授
1
一次函数的简单应用
练一练:
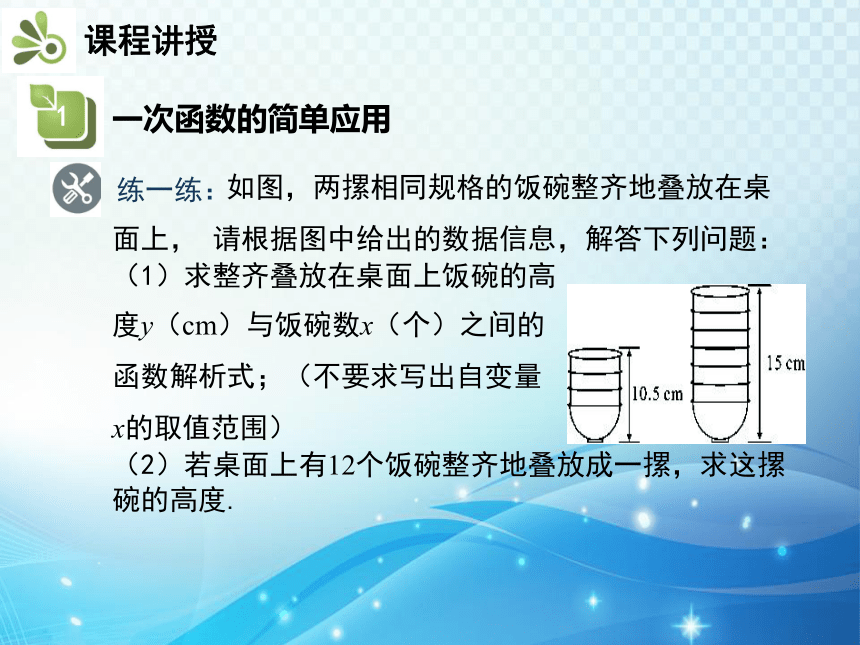
如图,两摞相同规格的饭碗整齐地叠放在桌面上, 请根据图中给出的数据信息,解答下列问题:
(1)求整齐叠放在桌面上饭碗的高
度y(cm)与饭碗数x(个)之间的
函数解析式;(不要求写出自变量
x的取值范围)
(2)若桌面上有12个饭碗整齐地叠放成一摞,求这摞碗的高度.
课程讲授
1
一次函数的简单应用
练一练:
解:(1)设函数解析式为y= kx + b,根据题意,得
4k+b=10. 5,
7k+b=15,
解得 k=1.5,
b = 4. 5,
∴y与x之间的函数解析式为y = 1.5x+ 4. 5.
(2)当 x=12 时,y= 1. 5×12 + 4. 5 = 22. 5.
答:这摞碗的高度是22. 5 cm.
例
课程讲授
2
分段函数的应用
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
“黄金1号”玉米种子的价格为5 元/kg,如果一次购 买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
2.5
5
7.5
10
12
14
16
18
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
提示:付款金额与种子价格相关.问题中种子价格不是固定不变的,它与购买量有关.设购买x kg种子,当0≤x≤2时,种子价格为5元/kg;当x>2时,其中有2kg种子按5元/kg计价,其余的(x-2)kg(即超出2kg部分)种子按4元/kg(即8折)计价.因此,写函数解析式与画函数图象时,应对0≤x≤2和x>2分段讨论.
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x kg,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
函数图象为:
课程讲授
2
分段函数的应用
想一想:
你能由上面的函数解析式或函数图象解决以下问题吗?
由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)一次购买3 kg 种子,需付款多少元?
课程讲授
2
分段函数的应用
练一练:
如图是某复印店复印收费y(元)与复印页数(8开纸)x(页)的函数图象,那么从图象中可看出,复印超过100页的部分,每页收费( )
A. 0. 4 元 B. 0. 45 元
C.0.47 元 D.0.5 元
A
随堂练习
1.某水库的水位在5 h内持续上涨,初始的水位高度为6 m,水位以每小时0. 3 m的速度匀速上升,则 水库的水位高度y m与时间x h(0≤x≤5)的函数关系式为 .
y=6+0.3x
随堂练习
2.
(中考·阜新)一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前_____h到达B地.
2
随堂练习
3.有一个安装进出水管的30 L容器,水管单位时间
内进出的水量是一定的,设从某时刻开始的4 min内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(L)与时间x(min)之间的函数关系如图所示.下列说法错误的是( )
A.每分钟进水5 L
B.每分钟放水1.25 L
C.若12 min后只放水,不进水,
还要8 min可以把水放完
D.若从一开始进出水管同时打开需要24 min可以
将容器灌满
B
随堂练习
4.(中考 .绍兴)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(kw .h)关于已行驶路程x(km)的函数图象.
(1) 根据图象,直接写出蓄电池剩余电量为35 kw .h时汽车已行驶的路程.当0≤x≤150时, 求1 kw .h的电量汽车能行驶的路程;
(1)由图象可知,蓄电池剩余电量为35
kw h时汽车已行驶了150 km.1 kw h的电量汽车能行驶的路程为 =6(km).
解:
随堂练习
(2) 当150≤x≤200时,求y关于x的函数解析式,并计算当汽车已行驶180 km时,蓄电池的剩余电量.
(2)设y关于x的函数解析式为y= kx + b,把点(150,35),(200,10)代入,得
解得 ∴y=-0.5x+110.
当 x= 180 时,y=-0. 5×180 + 110 = 20.
解:
150k+b=35,
200k+b=10,
k=-0.5,
b=110,
课堂小结
一次函数的实际应用
一次函数的简单应用
分段函数的应用
19.2 一次函数
19.2.2 一次函数
第十九章 一次函数
课程讲授
新知导入
随堂练习
课堂小结
第4课时 一次函数的实际应用
知识要点
1.一次函数的简单应用
2.分段函数的应用
新知导入
看一看:
利用函数方法解决实际问题,关键是分析题中的
数量关系,联系实际生活及以前学过的内容,将
实际问题抽象、升华为一次函数模型,即建模,
再利用函数的性质解决问题.一次函数的应用主
要有两种类型:
新知导入
看一看:
(1)给出了一次函数关系式,直接应用一次函数
的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数
的情境时,应先求出关系式,进而利用函数
性质解决问题.
例 某弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如图所示,当所挂物体质量为20 kg时,弹簧的长度为( )
A. 20 cm
B. 25 cm
C. 30 cm
D.无法确定
课程讲授
1
一次函数的简单应用
A
课程讲授
1
一次函数的简单应用
练一练:
如图,两摞相同规格的饭碗整齐地叠放在桌面上, 请根据图中给出的数据信息,解答下列问题:
(1)求整齐叠放在桌面上饭碗的高
度y(cm)与饭碗数x(个)之间的
函数解析式;(不要求写出自变量
x的取值范围)
(2)若桌面上有12个饭碗整齐地叠放成一摞,求这摞碗的高度.
课程讲授
1
一次函数的简单应用
练一练:
解:(1)设函数解析式为y= kx + b,根据题意,得
4k+b=10. 5,
7k+b=15,
解得 k=1.5,
b = 4. 5,
∴y与x之间的函数解析式为y = 1.5x+ 4. 5.
(2)当 x=12 时,y= 1. 5×12 + 4. 5 = 22. 5.
答:这摞碗的高度是22. 5 cm.
例
课程讲授
2
分段函数的应用
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
“黄金1号”玉米种子的价格为5 元/kg,如果一次购 买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
2.5
5
7.5
10
12
14
16
18
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
提示:付款金额与种子价格相关.问题中种子价格不是固定不变的,它与购买量有关.设购买x kg种子,当0≤x≤2时,种子价格为5元/kg;当x>2时,其中有2kg种子按5元/kg计价,其余的(x-2)kg(即超出2kg部分)种子按4元/kg(即8折)计价.因此,写函数解析式与画函数图象时,应对0≤x≤2和x>2分段讨论.
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x kg,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
例
课程讲授
2
分段函数的应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
函数图象为:
课程讲授
2
分段函数的应用
想一想:
你能由上面的函数解析式或函数图象解决以下问题吗?
由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)一次购买3 kg 种子,需付款多少元?
课程讲授
2
分段函数的应用
练一练:
如图是某复印店复印收费y(元)与复印页数(8开纸)x(页)的函数图象,那么从图象中可看出,复印超过100页的部分,每页收费( )
A. 0. 4 元 B. 0. 45 元
C.0.47 元 D.0.5 元
A
随堂练习
1.某水库的水位在5 h内持续上涨,初始的水位高度为6 m,水位以每小时0. 3 m的速度匀速上升,则 水库的水位高度y m与时间x h(0≤x≤5)的函数关系式为 .
y=6+0.3x
随堂练习
2.
(中考·阜新)一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前_____h到达B地.
2
随堂练习
3.有一个安装进出水管的30 L容器,水管单位时间
内进出的水量是一定的,设从某时刻开始的4 min内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(L)与时间x(min)之间的函数关系如图所示.下列说法错误的是( )
A.每分钟进水5 L
B.每分钟放水1.25 L
C.若12 min后只放水,不进水,
还要8 min可以把水放完
D.若从一开始进出水管同时打开需要24 min可以
将容器灌满
B
随堂练习
4.(中考 .绍兴)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(kw .h)关于已行驶路程x(km)的函数图象.
(1) 根据图象,直接写出蓄电池剩余电量为35 kw .h时汽车已行驶的路程.当0≤x≤150时, 求1 kw .h的电量汽车能行驶的路程;
(1)由图象可知,蓄电池剩余电量为35
kw h时汽车已行驶了150 km.1 kw h的电量汽车能行驶的路程为 =6(km).
解:
随堂练习
(2) 当150≤x≤200时,求y关于x的函数解析式,并计算当汽车已行驶180 km时,蓄电池的剩余电量.
(2)设y关于x的函数解析式为y= kx + b,把点(150,35),(200,10)代入,得
解得 ∴y=-0.5x+110.
当 x= 180 时,y=-0. 5×180 + 110 = 20.
解:
150k+b=35,
200k+b=10,
k=-0.5,
b=110,
课堂小结
一次函数的实际应用
一次函数的简单应用
分段函数的应用
