人教版(2023春)数学五年级下册4.7最小公倍数 课件(36张PPT)
文档属性
| 名称 | 人教版(2023春)数学五年级下册4.7最小公倍数 课件(36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
第4单元 分数的意义和性质
第7节 最小公倍数
规则:先请同学们报数,要声音洪亮,口齿清楚,并记住自己所报的数;再请报2的倍数的同学起立,几秒钟后坐下;最后请报3的倍数的同学起立,然后坐下。
以趣激疑
小游戏
你发现了什么 为什么有些人起立了两次
以趣激疑
有些数既是2的倍数又是3的倍数。
6,12,18,24,…既是2的倍数又是3的倍数,我们就可以说6,12,18,24,…是2和3的公倍数。
以趣激疑
今天我们就一起来研究有关公倍数的问题。
探究新知
姜子牙没出道前,住在一个村子里。村子里有个胖胖的地主,找了一些人给他家做长工。有一年,这些长工在胖地主家做了一年也没拿到一个铜板,心里又着急又生气。于是长工们自发地组织起来,并邀请姜子牙帮他们去向胖地主讨工钱。胖地主含着烟斗冷笑着说:“工钱我可以给你们,不过我的钱都在我的账房先生那里。从八月一日起,我要连续出去收账3天才休息一天,我的账房先生要连续收账5天才可以休息一天,你们就在我们两人同时休息的时候来吧。我肯定给钱。”姜子牙想了想,便带长工们离开了。到了某天,他真的从胖地主家帮长工们拿到了工钱。
小故事
探究新知
请大家想一想,姜子牙是哪天去胖地主家的 他用的是什么办法找到这个日期的 你准备如何解决这个问题
要先分别找出胖地主、账房先生的休息日,再找出他们两人的共同休息日。
特别提醒:休息日的日期应是4和6的公倍数,而不是3和5的公倍数。
账房先生的休息日
××
胖地主的休息日
××
探究新知
探究新知
胖地主和账房先生的共同休息日是12日、24日。
姜子牙只有在胖地主和账房先生都在家休息的日子去才能拿到钱,所以姜子牙可以在12日或24日去找胖地主和账房先生。
探究新知
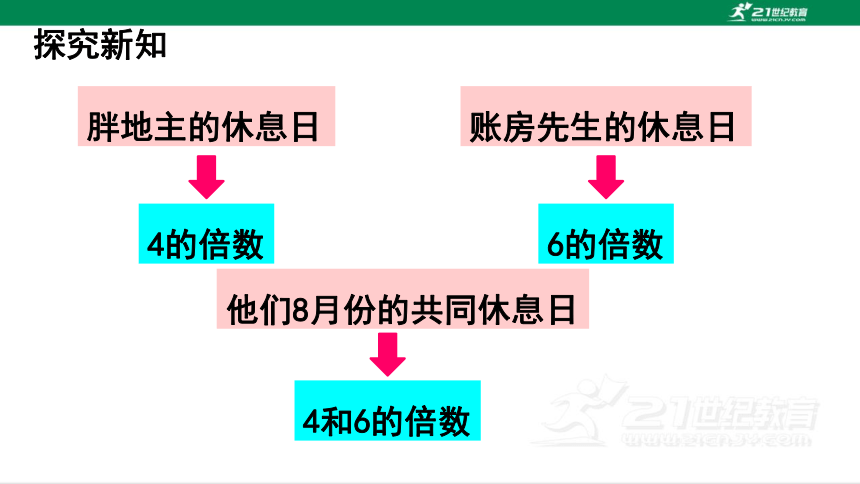
胖地主的休息日
账房先生的休息日
他们8月份的共同休息日
4的倍数
6的倍数
4和6的倍数
探究新知
“4和6的倍数”还可以怎么说
数据“12”是什么
4和6的公倍数
“公”是什么意思
你有我也有
4和6的最小公倍数
探究新知
4的倍数
4,8,16,20,28,32,40,…
12,24,
36,…
集合图的表示方式
6的倍数
6,18,
30,42,…
4和6的公倍数
探究新知
什么是公倍数 什么是最小公倍数
12,24,36,…是4和6公有的倍数,叫作它们的公倍数。
1
2
其中,12是最小的公倍数,叫作它们的最小公倍数。
探究新知
一些小朋友在组织跳绳活动。他们可以分成6人一组,也可以分成8人一组,都正好分完。
猜猜这些小朋友可能有几人。
要求人数就是求6和8的公倍数。
探究新知
6的倍数:6,12,18,24,30,36,42,48,…
8的倍数:8,16,24,32,40,48,…
1
2
8的倍数:8,16,24,32,40,48,…
探究新知
观察一下,两个数的公倍数和它们的最小公倍数之间有什么关系
48÷24=2,它们是倍数关系,两个数的公倍数都是最小公倍数的倍数。
6和8的公倍数:24,48,72,96,…
6和8的最小公倍数:24
探究新知
还有其他方法求两个数的公倍数和最小公倍数吗
探究新知
要求两个数的最小公倍数,可将较大数翻倍,一直翻倍到是较小数的倍数时,那这个数就是这两个数的最小公倍数。
42是6的倍数,那么42就是6和7的最小公倍数。
如:6和7
7×1=7
7×2=14
7×3=21
7×4=28
7×5=35
7×6=42
……
(1)大数翻倍的方法
探究新知
可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。
例如:60=2×2×3×5
42=2×3×7
60和42的最小公倍数:2×3×2×5×7=420
(2)短除法
探究新知
为了简便,可以写成下面的形式:
(2)短除法
60和42的最小公倍数:2×3×10×7=420
2 60 42
…用公有的质因数2除
3 30 21
…用公有的质因数3除
10 7 …除到两个商只有公因数1为止
探究新知
如果这些小朋友的总人数在50以内,那么他们最多有几人
48人
一些小朋友在组织跳绳活动。他们可以分成6人一组,也可以分成8人一组,都正好分完。
探究新知
我们所求出的“48人”是6和8的最大公倍数吗 为什么 为什么不用学习求最大公倍数呢
每一个数的倍数的个数都是无限的,两个数的公倍数的个数也是无限的。因此,两个数没有最大公倍数
探究新知
想一想找“共同的休息日”和“人数”的过程,说一说,可以怎样求两个数的最小公倍数
探究新知
求最小公倍数的方法
①找倍数:从小到大依次找出各个数的倍数;
②找公倍数:把各个数的倍数进行对照,找出公倍数;
③找最小公倍数:从公倍数中找出最小的那个)。
探究新知
你从中了解到哪些数学信息
例3 一种长方形地砖长3 dm,宽2 dm。如果用
这种地砖铺一个正方形(用的地砖必须都
是整块的),正方形的边长可以是多少分
米 最小是多少分米
怎样解决这个问题呢
探究新知
铺成的正方形可能有很多种。
1
2
要用整块的这种长方形地砖铺出一个正方形。
探究新知
正方形的边长必须既是3的倍数,又是2的倍数。
3
4
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长了。
探究新知
2和3的公倍数有哪些 最小公倍数是多少?
2和3的公倍数有6,12,18,24,…
你知道要铺出正方形的边长是多少了吗
正方形的边长可以是6 dm、12 dm、18 dm……最小是6 dm。
在边长是6 dm的正方形上画一画,看看找得对不对。
探究新知
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
深化理解
找出下列每组数的最小公倍数。你发现了什么
观察一下,每一组中的两个数有什么关系 它们的最小公倍数与这两个数有什么关系
3和6
2和8
4和9
6
8
36
3和9
5和6
9
5和10
10
30
深化理解
将题中的数分为两组:
第一组:3和6 2和8 3和9 5和10
第二组:5和6 4和9
观察第一组,它们的最小公倍数有什么规律吗
一个数是另一个数的倍数,它们的最小公倍数就是其中较大的那个数。
深化理解
第二组:5和6 4和9
当两个数是互质数时,它们的最小公倍数就是这两个数的积。
5和6的最小公倍数是30,4和9的最小公倍数是36,它们的最小公倍数有什么规律吗 你们能举出类似的两个数,并说出它们的最小公倍数吗
课堂练习
1.按照从小到大的顺序,在100以内的数中找出6的倍
数和10的倍数,再找出它们的公倍数和最小公倍数。
6的倍数:6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96。
公倍数:30,60,90。最小公倍数:30。
10的倍数:10,20,30,40,50,60,70,80,90,100。
课堂练习
2.找出下列每组数的最小公倍数。
8和10
6和15
4和15
40
30
60
1和7
6和9
7
4和10
20
18
课堂小结
今天你学到了什么 收获最大的是什么 你有什么学习经验介绍给大家
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4单元 分数的意义和性质
第7节 最小公倍数
规则:先请同学们报数,要声音洪亮,口齿清楚,并记住自己所报的数;再请报2的倍数的同学起立,几秒钟后坐下;最后请报3的倍数的同学起立,然后坐下。
以趣激疑
小游戏
你发现了什么 为什么有些人起立了两次
以趣激疑
有些数既是2的倍数又是3的倍数。
6,12,18,24,…既是2的倍数又是3的倍数,我们就可以说6,12,18,24,…是2和3的公倍数。
以趣激疑
今天我们就一起来研究有关公倍数的问题。
探究新知
姜子牙没出道前,住在一个村子里。村子里有个胖胖的地主,找了一些人给他家做长工。有一年,这些长工在胖地主家做了一年也没拿到一个铜板,心里又着急又生气。于是长工们自发地组织起来,并邀请姜子牙帮他们去向胖地主讨工钱。胖地主含着烟斗冷笑着说:“工钱我可以给你们,不过我的钱都在我的账房先生那里。从八月一日起,我要连续出去收账3天才休息一天,我的账房先生要连续收账5天才可以休息一天,你们就在我们两人同时休息的时候来吧。我肯定给钱。”姜子牙想了想,便带长工们离开了。到了某天,他真的从胖地主家帮长工们拿到了工钱。
小故事
探究新知
请大家想一想,姜子牙是哪天去胖地主家的 他用的是什么办法找到这个日期的 你准备如何解决这个问题
要先分别找出胖地主、账房先生的休息日,再找出他们两人的共同休息日。
特别提醒:休息日的日期应是4和6的公倍数,而不是3和5的公倍数。
账房先生的休息日
××
胖地主的休息日
××
探究新知
探究新知
胖地主和账房先生的共同休息日是12日、24日。
姜子牙只有在胖地主和账房先生都在家休息的日子去才能拿到钱,所以姜子牙可以在12日或24日去找胖地主和账房先生。
探究新知
胖地主的休息日
账房先生的休息日
他们8月份的共同休息日
4的倍数
6的倍数
4和6的倍数
探究新知
“4和6的倍数”还可以怎么说
数据“12”是什么
4和6的公倍数
“公”是什么意思
你有我也有
4和6的最小公倍数
探究新知
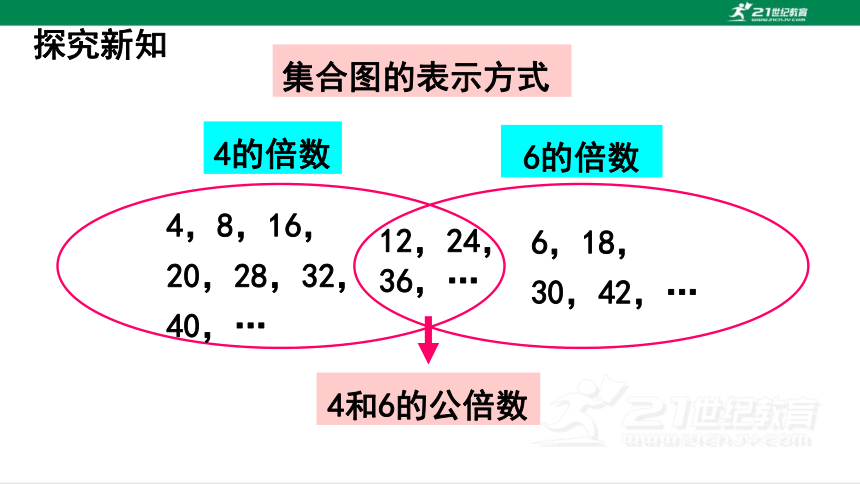
4的倍数
4,8,16,20,28,32,40,…
12,24,
36,…
集合图的表示方式
6的倍数
6,18,
30,42,…
4和6的公倍数
探究新知
什么是公倍数 什么是最小公倍数
12,24,36,…是4和6公有的倍数,叫作它们的公倍数。
1
2
其中,12是最小的公倍数,叫作它们的最小公倍数。
探究新知
一些小朋友在组织跳绳活动。他们可以分成6人一组,也可以分成8人一组,都正好分完。
猜猜这些小朋友可能有几人。
要求人数就是求6和8的公倍数。
探究新知
6的倍数:6,12,18,24,30,36,42,48,…
8的倍数:8,16,24,32,40,48,…
1
2
8的倍数:8,16,24,32,40,48,…
探究新知
观察一下,两个数的公倍数和它们的最小公倍数之间有什么关系
48÷24=2,它们是倍数关系,两个数的公倍数都是最小公倍数的倍数。
6和8的公倍数:24,48,72,96,…
6和8的最小公倍数:24
探究新知
还有其他方法求两个数的公倍数和最小公倍数吗
探究新知
要求两个数的最小公倍数,可将较大数翻倍,一直翻倍到是较小数的倍数时,那这个数就是这两个数的最小公倍数。
42是6的倍数,那么42就是6和7的最小公倍数。
如:6和7
7×1=7
7×2=14
7×3=21
7×4=28
7×5=35
7×6=42
……
(1)大数翻倍的方法
探究新知
可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。
例如:60=2×2×3×5
42=2×3×7
60和42的最小公倍数:2×3×2×5×7=420
(2)短除法
探究新知
为了简便,可以写成下面的形式:
(2)短除法
60和42的最小公倍数:2×3×10×7=420
2 60 42
…用公有的质因数2除
3 30 21
…用公有的质因数3除
10 7 …除到两个商只有公因数1为止
探究新知
如果这些小朋友的总人数在50以内,那么他们最多有几人
48人
一些小朋友在组织跳绳活动。他们可以分成6人一组,也可以分成8人一组,都正好分完。
探究新知
我们所求出的“48人”是6和8的最大公倍数吗 为什么 为什么不用学习求最大公倍数呢
每一个数的倍数的个数都是无限的,两个数的公倍数的个数也是无限的。因此,两个数没有最大公倍数
探究新知
想一想找“共同的休息日”和“人数”的过程,说一说,可以怎样求两个数的最小公倍数
探究新知
求最小公倍数的方法
①找倍数:从小到大依次找出各个数的倍数;
②找公倍数:把各个数的倍数进行对照,找出公倍数;
③找最小公倍数:从公倍数中找出最小的那个)。
探究新知
你从中了解到哪些数学信息
例3 一种长方形地砖长3 dm,宽2 dm。如果用
这种地砖铺一个正方形(用的地砖必须都
是整块的),正方形的边长可以是多少分
米 最小是多少分米
怎样解决这个问题呢
探究新知
铺成的正方形可能有很多种。
1
2
要用整块的这种长方形地砖铺出一个正方形。
探究新知
正方形的边长必须既是3的倍数,又是2的倍数。
3
4
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长了。
探究新知
2和3的公倍数有哪些 最小公倍数是多少?
2和3的公倍数有6,12,18,24,…
你知道要铺出正方形的边长是多少了吗
正方形的边长可以是6 dm、12 dm、18 dm……最小是6 dm。
在边长是6 dm的正方形上画一画,看看找得对不对。
探究新知
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
深化理解
找出下列每组数的最小公倍数。你发现了什么
观察一下,每一组中的两个数有什么关系 它们的最小公倍数与这两个数有什么关系
3和6
2和8
4和9
6
8
36
3和9
5和6
9
5和10
10
30
深化理解
将题中的数分为两组:
第一组:3和6 2和8 3和9 5和10
第二组:5和6 4和9
观察第一组,它们的最小公倍数有什么规律吗
一个数是另一个数的倍数,它们的最小公倍数就是其中较大的那个数。
深化理解
第二组:5和6 4和9
当两个数是互质数时,它们的最小公倍数就是这两个数的积。
5和6的最小公倍数是30,4和9的最小公倍数是36,它们的最小公倍数有什么规律吗 你们能举出类似的两个数,并说出它们的最小公倍数吗
课堂练习
1.按照从小到大的顺序,在100以内的数中找出6的倍
数和10的倍数,再找出它们的公倍数和最小公倍数。
6的倍数:6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96。
公倍数:30,60,90。最小公倍数:30。
10的倍数:10,20,30,40,50,60,70,80,90,100。
课堂练习
2.找出下列每组数的最小公倍数。
8和10
6和15
4和15
40
30
60
1和7
6和9
7
4和10
20
18
课堂小结
今天你学到了什么 收获最大的是什么 你有什么学习经验介绍给大家
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
