2022-2023学年北师大版九年级数学下册2.2 二次函数的图象与性质 强化训练(无答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册2.2 二次函数的图象与性质 强化训练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 21:53:54 | ||
图片预览

文档简介
2.2 二次函数的图象与性质( 强化训练)-北师大版九年级下册
一.选择题
.二次函数y=ax2+bx+c(a≠0)的图象如图所示,点P在x轴的正半轴上,下列选项中正确的是( )
A.a>0 B.c<0 C.a+b+c>0 D.b<0
.将抛物线经过下列平移能得到抛物线的是( )
A.向右平移1个单位,向下平移3个单位
B.向左平移1个单位,向下平移3个单位
C.向右平移1个单位,向上平移3个单位
D.向左平移1个单位,向上平移3个单位
.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
A. B.
C. D.
.已知抛物线y=(2﹣a)x2+1有最低点,那么a的取值范围是( )
A.a>0 B.a<0 C.a>2 D.a<2
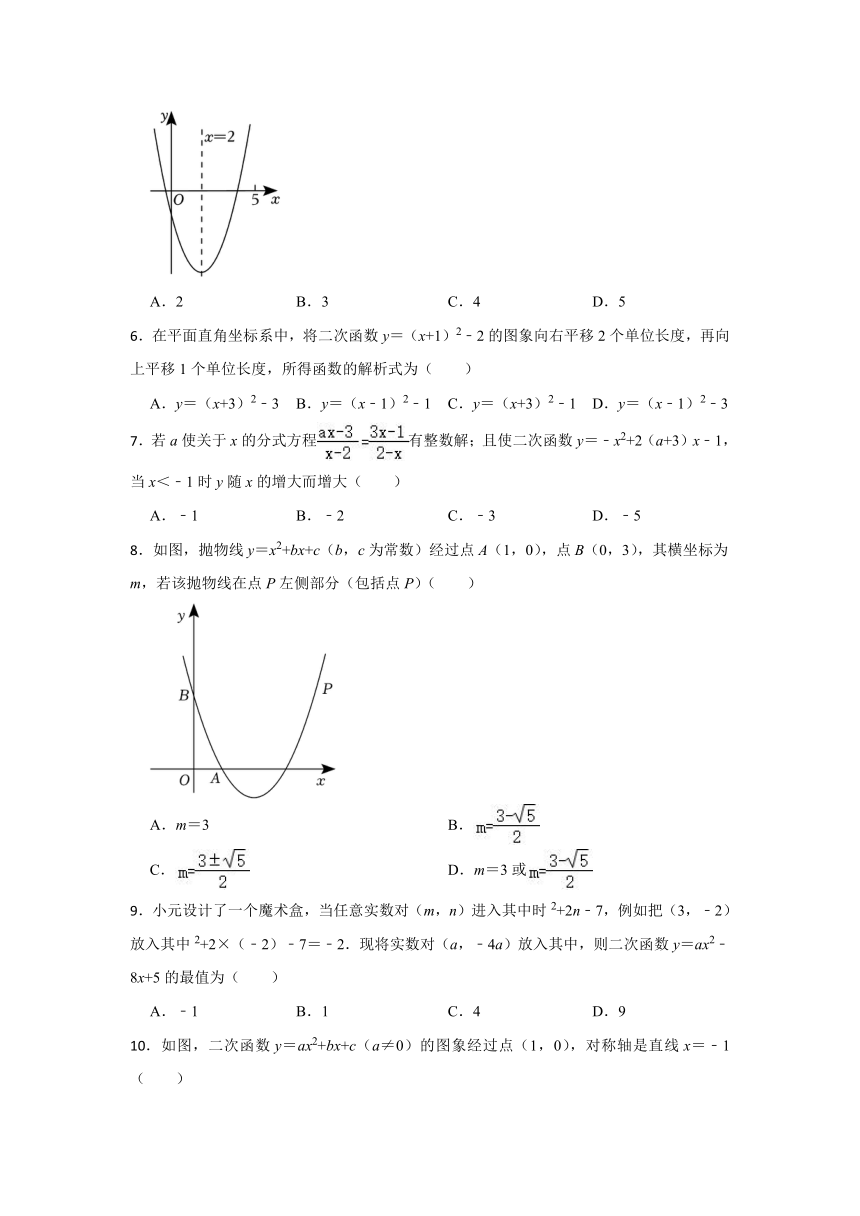
.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,下列结论:①abc>0;③a﹣b+c>0;④;⑤若P(﹣4,y1),Q(8,y2)是该函数图象上两点,则y1=y2.正确结论的个数是( )
A.2 B.3 C.4 D.5
.在平面直角坐标系中,将二次函数y=(x+1)2﹣2的图象向右平移2个单位长度,再向上平移1个单位长度,所得函数的解析式为( )
A.y=(x+3)2﹣3 B.y=(x﹣1)2﹣1 C.y=(x+3)2﹣1 D.y=(x﹣1)2﹣3
.若a使关于x的分式方程有整数解;且使二次函数y=﹣x2+2(a+3)x﹣1,当x<﹣1时y随x的增大而增大( )
A.﹣1 B.﹣2 C.﹣3 D.﹣5
.如图,抛物线y=x2+bx+c(b,c为常数)经过点A(1,0),点B(0,3),其横坐标为m,若该抛物线在点P左侧部分(包括点P)( )
A.m=3 B.
C. D.m=3或
.小元设计了一个魔术盒,当任意实数对(m,n)进入其中时2+2n﹣7,例如把(3,﹣2)放入其中2+2×(﹣2)﹣7=﹣2.现将实数对(a,﹣4a)放入其中,则二次函数y=ax2﹣8x+5的最值为( )
A.﹣1 B.1 C.4 D.9
.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),对称轴是直线x=﹣1( )
A.abc>0 B.2a﹣b=0 C.3a+2c<0 D.9a﹣3b+c=0
二.填空题
.二次函数y=ax2+2ax+c(a<0)图象上两点的坐标分别为(﹣1,y1),(2,y2),则y1和y2大小关系是 .
.用一张边长为48cm的正方形纸,制成一个无盖的长方体盒子,需在四个角上都剪去一个同样大小的正方形(如图中虚线所示),折成的无盖的长方体的容积是 立方厘米;用你喜欢的方式探究,用这张正方形纸可制成的无盖的长方体盒子的最大容积是 立方厘米.
.若实数a,b满足a+b2=2b+1,则代数式a2﹣4a+2b2﹣4b﹣4的最小值为 .
.已知二次函数y=a(x﹣2)2+a(a<0),当﹣1≤x≤4时,y的最小值为﹣10 .
.已知A(x1,y1),B(x2,y2)是抛物线y=ax2﹣3x+1上的两点,其对称轴是直线x=x0,若|x1﹣x0|>|x2﹣x0|时,总有y1>y2,同一坐标系中有M(﹣1,﹣2),N(3,2),且抛物线y=ax2﹣3x+1与线段MN有两个不相同的交点,则a的取值范围是 .
三.解答题
.已知二次函数y=x2﹣2x﹣4.
(1)求该函数图象的顶点坐标和对称轴.
(2)自变量在什么范围内时,y随x的增大而增大.
.如图,点P(a,3)在抛物线C:y=4﹣(7﹣x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',使C'所在抛物线对应的函数恰为y=﹣x2+8x﹣16,求点P'移动的最短路程.
.已知二次函数y=x2﹣2x+c的图象如图所示.
(1)求该抛物线的顶点坐标;
(2)将该抛物线进行左右平移,使其经过坐标原点,请直接写出平移的方法.
.在平面直角坐标系xOy中,已知抛物线M:y=ax2﹣4ax+4a+1(a≠0)和直线l:y=.
(1)抛物线M的对称轴是 ;
(2)若直线y=n与抛物线M有两个公共点,它们的横坐标记为x1,x2,直线y=n与直线l的交点横坐标记为x3.若当﹣1<n<0时,总有x1<x3<x2,请结合函数图象,求a的取值范围.
.两个完全相同的长方形ABCD、EFGH,如图所示放置在数轴上.
(1)长方形ABCD的面积是 .
(2)若点P在线段BE上,且PA+PB=5,求点P在数轴上表示的数.
(3)若长方形ABCD、EFGH分别以每秒2个单位长度、1个单位长度在数轴上相向而行.设两个长方形重叠部分的面积为S,移动时间为t.
①在整个运动过程中,S的最大值是 ,持续时间是 ;
②当S是长方形ABCD面积一半时,求t的值.
一.选择题
.二次函数y=ax2+bx+c(a≠0)的图象如图所示,点P在x轴的正半轴上,下列选项中正确的是( )
A.a>0 B.c<0 C.a+b+c>0 D.b<0
.将抛物线经过下列平移能得到抛物线的是( )
A.向右平移1个单位,向下平移3个单位
B.向左平移1个单位,向下平移3个单位
C.向右平移1个单位,向上平移3个单位
D.向左平移1个单位,向上平移3个单位
.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
A. B.
C. D.
.已知抛物线y=(2﹣a)x2+1有最低点,那么a的取值范围是( )
A.a>0 B.a<0 C.a>2 D.a<2
.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,下列结论:①abc>0;③a﹣b+c>0;④;⑤若P(﹣4,y1),Q(8,y2)是该函数图象上两点,则y1=y2.正确结论的个数是( )
A.2 B.3 C.4 D.5
.在平面直角坐标系中,将二次函数y=(x+1)2﹣2的图象向右平移2个单位长度,再向上平移1个单位长度,所得函数的解析式为( )
A.y=(x+3)2﹣3 B.y=(x﹣1)2﹣1 C.y=(x+3)2﹣1 D.y=(x﹣1)2﹣3
.若a使关于x的分式方程有整数解;且使二次函数y=﹣x2+2(a+3)x﹣1,当x<﹣1时y随x的增大而增大( )
A.﹣1 B.﹣2 C.﹣3 D.﹣5
.如图,抛物线y=x2+bx+c(b,c为常数)经过点A(1,0),点B(0,3),其横坐标为m,若该抛物线在点P左侧部分(包括点P)( )
A.m=3 B.
C. D.m=3或
.小元设计了一个魔术盒,当任意实数对(m,n)进入其中时2+2n﹣7,例如把(3,﹣2)放入其中2+2×(﹣2)﹣7=﹣2.现将实数对(a,﹣4a)放入其中,则二次函数y=ax2﹣8x+5的最值为( )
A.﹣1 B.1 C.4 D.9
.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),对称轴是直线x=﹣1( )
A.abc>0 B.2a﹣b=0 C.3a+2c<0 D.9a﹣3b+c=0
二.填空题
.二次函数y=ax2+2ax+c(a<0)图象上两点的坐标分别为(﹣1,y1),(2,y2),则y1和y2大小关系是 .
.用一张边长为48cm的正方形纸,制成一个无盖的长方体盒子,需在四个角上都剪去一个同样大小的正方形(如图中虚线所示),折成的无盖的长方体的容积是 立方厘米;用你喜欢的方式探究,用这张正方形纸可制成的无盖的长方体盒子的最大容积是 立方厘米.
.若实数a,b满足a+b2=2b+1,则代数式a2﹣4a+2b2﹣4b﹣4的最小值为 .
.已知二次函数y=a(x﹣2)2+a(a<0),当﹣1≤x≤4时,y的最小值为﹣10 .
.已知A(x1,y1),B(x2,y2)是抛物线y=ax2﹣3x+1上的两点,其对称轴是直线x=x0,若|x1﹣x0|>|x2﹣x0|时,总有y1>y2,同一坐标系中有M(﹣1,﹣2),N(3,2),且抛物线y=ax2﹣3x+1与线段MN有两个不相同的交点,则a的取值范围是 .
三.解答题
.已知二次函数y=x2﹣2x﹣4.
(1)求该函数图象的顶点坐标和对称轴.
(2)自变量在什么范围内时,y随x的增大而增大.
.如图,点P(a,3)在抛物线C:y=4﹣(7﹣x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',使C'所在抛物线对应的函数恰为y=﹣x2+8x﹣16,求点P'移动的最短路程.
.已知二次函数y=x2﹣2x+c的图象如图所示.
(1)求该抛物线的顶点坐标;
(2)将该抛物线进行左右平移,使其经过坐标原点,请直接写出平移的方法.
.在平面直角坐标系xOy中,已知抛物线M:y=ax2﹣4ax+4a+1(a≠0)和直线l:y=.
(1)抛物线M的对称轴是 ;
(2)若直线y=n与抛物线M有两个公共点,它们的横坐标记为x1,x2,直线y=n与直线l的交点横坐标记为x3.若当﹣1<n<0时,总有x1<x3<x2,请结合函数图象,求a的取值范围.
.两个完全相同的长方形ABCD、EFGH,如图所示放置在数轴上.
(1)长方形ABCD的面积是 .
(2)若点P在线段BE上,且PA+PB=5,求点P在数轴上表示的数.
(3)若长方形ABCD、EFGH分别以每秒2个单位长度、1个单位长度在数轴上相向而行.设两个长方形重叠部分的面积为S,移动时间为t.
①在整个运动过程中,S的最大值是 ,持续时间是 ;
②当S是长方形ABCD面积一半时,求t的值.
