2022-2023学年人教版数学八年级下册第十八章 平行四边形 测试卷 (无答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级下册第十八章 平行四边形 测试卷 (无答案) | 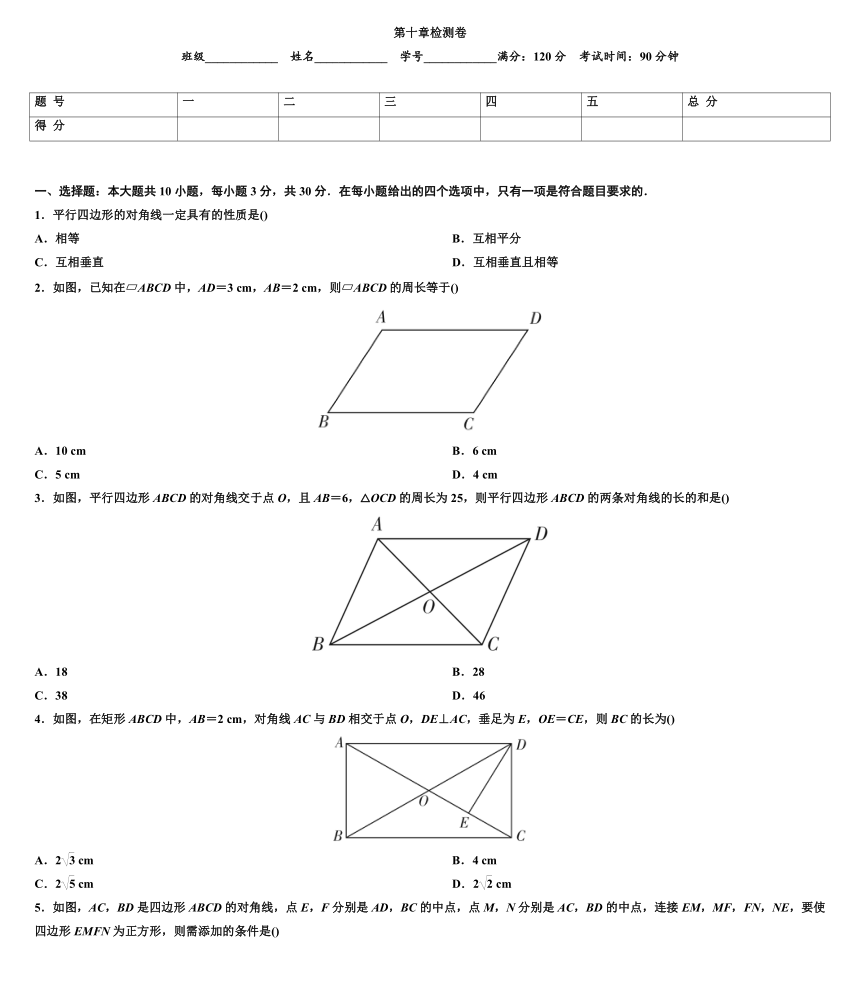 | |
| 格式 | docx | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 22:23:09 | ||
图片预览

文档简介
第十章检测卷
班级____________ 姓名____________ 学号____________满分:120分 考试时间:90分钟
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.平行四边形的对角线一定具有的性质是()
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
2.如图,已知在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长等于()
A.10 cm B.6 cm
C.5 cm D.4 cm
3.如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为25,则平行四边形ABCD的两条对角线的长的和是()
A.18 B.28
C.38 D.46
4.如图,在矩形ABCD中,AB=2 cm,对角线AC与BD相交于点O,DE⊥AC,垂足为E,OE=CE,则BC的长为()
A.2 cm B.4 cm
C.2 cm D.2 cm
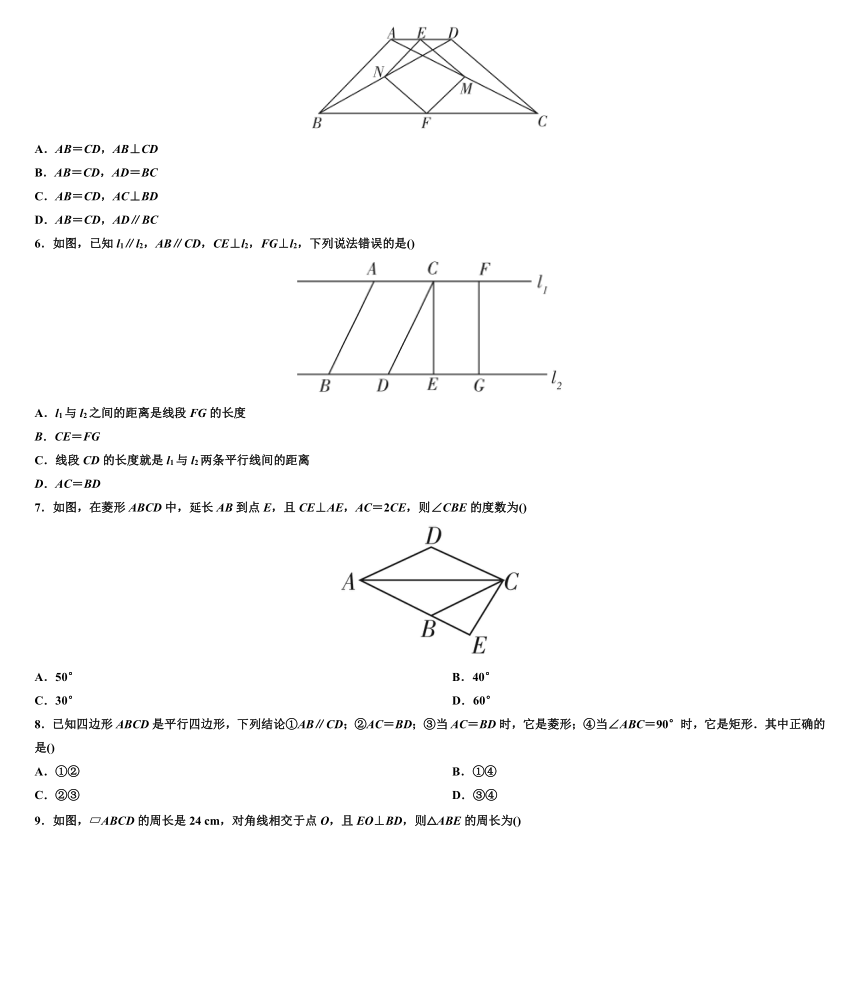
5.如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是()
A.AB=CD,AB⊥CD
B.AB=CD,AD=BC
C.AB=CD,AC⊥BD
D.AB=CD,AD∥BC
6.如图,已知l1∥l2,AB∥CD,CE⊥l2,FG⊥l2,下列说法错误的是()
A.l1与l2之间的距离是线段FG的长度
B.CE=FG
C.线段CD的长度就是l1与l2两条平行线间的距离
D.AC=BD
7.如图,在菱形ABCD中,延长AB到点E,且CE⊥AE,AC=2CE,则∠CBE的度数为()
A.50° B.40°
C.30° D.60°
8.已知四边形ABCD是平行四边形,下列结论①AB∥CD;②AC=BD;③当AC=BD时,它是菱形;④当∠ABC=90°时,它是矩形.其中正确的是()
A.①② B.①④
C.②③ D.③④
9.如图, ABCD的周长是24 cm,对角线相交于点O,且EO⊥BD,则△ABE的周长为()
A.24 cm B.15 cm
C.12 cm D.10 cm
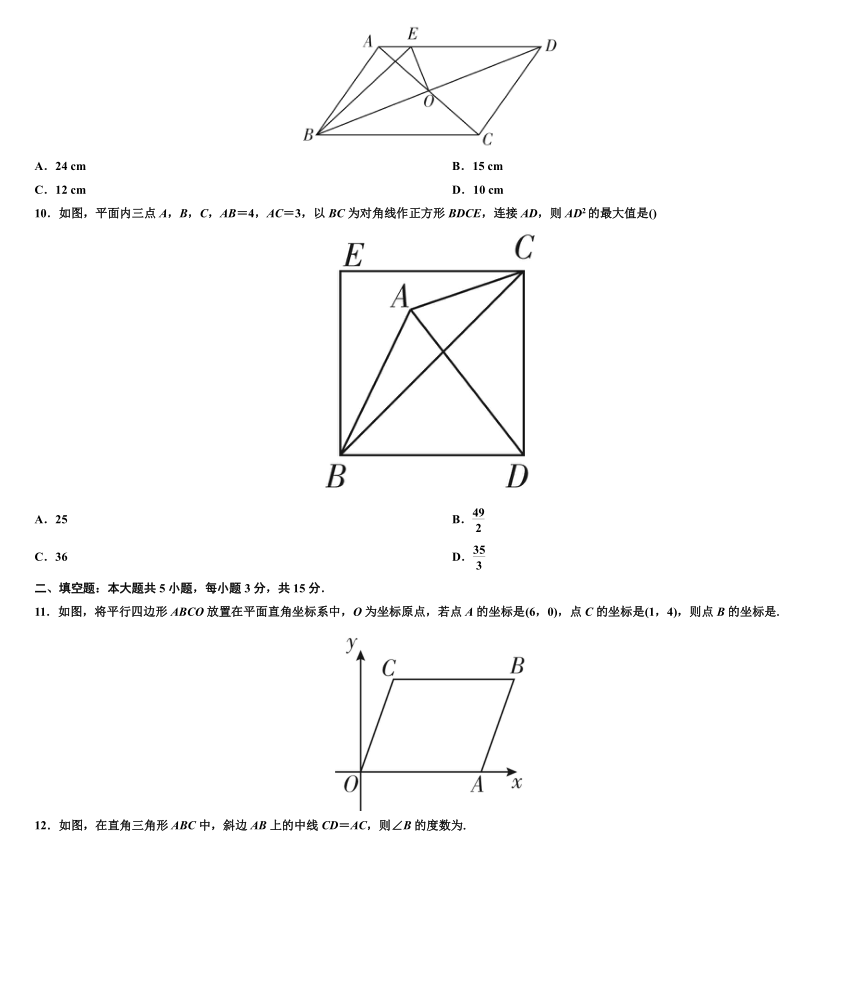
10.如图,平面内三点A,B,C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD2的最大值是()
A.25 B.
C.36 D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.如图,将平行四边形ABCO放置在平面直角坐标系中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是.
12.如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B的度数为.
13.菱形有一个内角是120°,有一条对角线为6 cm,则此菱形的边长是.
14.如图,将一张矩形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD.若∠ABC=58°,则∠E′BD的度数是.
15.如图,在菱形ABCD中,∠D=60°,CD=4,过AD的中点E作AC的垂线,交CB的延长线于点F.则EF的长为.
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.在四边形ABCD中,对角线AC,BD相交于点O,若AD=12,OD=OB=5,AC=26,∠ADB=90°,求证:四边形ABCD为平行四边形.
17.如图,在矩形ABCD中,点E在边AB上,连接DE,将矩形ABCD沿DE折叠,点A的对称点F落在边CD上,连接EF.求证:四边形ADFE是正方形.
18.如图,点E,F分别是锐角∠A两边上的点,分别以点E,F为圆心,以AF,AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)若AE=AF,请判断此四边形的形状,并说明理由.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,点O是菱形ABCD对角线的交点,CE∥BD,BE∥AC,连接OE.
(1)求证:OE=CB;
(2)若菱形的边长为2,∠ADC=60°,求四边形OCEB的面积.
20.如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而改变?并说明理由.
21.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD的中点,求证:四边形ABGE是平行四边形.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图,在正方形ABCD中,对角线交于点O,E是OB上一点,DG⊥AE于点G,DG交OA于点F.
(1)求证:OE=OF.
(2)当E为OB延长线上一点时,画出对应的图形.观察(1)中的结论是否仍然成立,并给予证明.
23.在平行四边形ABCD中,AB=6 cm,BC=a cm,P是对角线AC上的一个动点,由A向C运动(不与A,C重合),速度为每秒1 cm,Q是CB延长线上一点,与点P以相同的速度由B向CB延长线方向运动(不与B重合),连接PQ交AB于点E.
(1)如图①,若∠ABC=60°,BC=AB,求点P运动几秒后,∠BQE=30°.
(2)如图②,在(1)的条件下,作PF⊥AB于点F,在运动过程中,线段EF的长度是否发生变化?如果不变,求出EF的长;如果变化,请说明理由.
(3)如图③,当BC≠AB时,平行四边形的面积是24 cm2,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称?若存在,求出a的值;若不存在,说明理由.
班级____________ 姓名____________ 学号____________满分:120分 考试时间:90分钟
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.平行四边形的对角线一定具有的性质是()
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
2.如图,已知在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长等于()
A.10 cm B.6 cm
C.5 cm D.4 cm
3.如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为25,则平行四边形ABCD的两条对角线的长的和是()
A.18 B.28
C.38 D.46
4.如图,在矩形ABCD中,AB=2 cm,对角线AC与BD相交于点O,DE⊥AC,垂足为E,OE=CE,则BC的长为()
A.2 cm B.4 cm
C.2 cm D.2 cm
5.如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是()
A.AB=CD,AB⊥CD
B.AB=CD,AD=BC
C.AB=CD,AC⊥BD
D.AB=CD,AD∥BC
6.如图,已知l1∥l2,AB∥CD,CE⊥l2,FG⊥l2,下列说法错误的是()
A.l1与l2之间的距离是线段FG的长度
B.CE=FG
C.线段CD的长度就是l1与l2两条平行线间的距离
D.AC=BD
7.如图,在菱形ABCD中,延长AB到点E,且CE⊥AE,AC=2CE,则∠CBE的度数为()
A.50° B.40°
C.30° D.60°
8.已知四边形ABCD是平行四边形,下列结论①AB∥CD;②AC=BD;③当AC=BD时,它是菱形;④当∠ABC=90°时,它是矩形.其中正确的是()
A.①② B.①④
C.②③ D.③④
9.如图, ABCD的周长是24 cm,对角线相交于点O,且EO⊥BD,则△ABE的周长为()
A.24 cm B.15 cm
C.12 cm D.10 cm
10.如图,平面内三点A,B,C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD2的最大值是()
A.25 B.
C.36 D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.如图,将平行四边形ABCO放置在平面直角坐标系中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是.
12.如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B的度数为.
13.菱形有一个内角是120°,有一条对角线为6 cm,则此菱形的边长是.
14.如图,将一张矩形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD.若∠ABC=58°,则∠E′BD的度数是.
15.如图,在菱形ABCD中,∠D=60°,CD=4,过AD的中点E作AC的垂线,交CB的延长线于点F.则EF的长为.
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.在四边形ABCD中,对角线AC,BD相交于点O,若AD=12,OD=OB=5,AC=26,∠ADB=90°,求证:四边形ABCD为平行四边形.
17.如图,在矩形ABCD中,点E在边AB上,连接DE,将矩形ABCD沿DE折叠,点A的对称点F落在边CD上,连接EF.求证:四边形ADFE是正方形.
18.如图,点E,F分别是锐角∠A两边上的点,分别以点E,F为圆心,以AF,AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)若AE=AF,请判断此四边形的形状,并说明理由.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,点O是菱形ABCD对角线的交点,CE∥BD,BE∥AC,连接OE.
(1)求证:OE=CB;
(2)若菱形的边长为2,∠ADC=60°,求四边形OCEB的面积.
20.如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而改变?并说明理由.
21.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD的中点,求证:四边形ABGE是平行四边形.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图,在正方形ABCD中,对角线交于点O,E是OB上一点,DG⊥AE于点G,DG交OA于点F.
(1)求证:OE=OF.
(2)当E为OB延长线上一点时,画出对应的图形.观察(1)中的结论是否仍然成立,并给予证明.
23.在平行四边形ABCD中,AB=6 cm,BC=a cm,P是对角线AC上的一个动点,由A向C运动(不与A,C重合),速度为每秒1 cm,Q是CB延长线上一点,与点P以相同的速度由B向CB延长线方向运动(不与B重合),连接PQ交AB于点E.
(1)如图①,若∠ABC=60°,BC=AB,求点P运动几秒后,∠BQE=30°.
(2)如图②,在(1)的条件下,作PF⊥AB于点F,在运动过程中,线段EF的长度是否发生变化?如果不变,求出EF的长;如果变化,请说明理由.
(3)如图③,当BC≠AB时,平行四边形的面积是24 cm2,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称?若存在,求出a的值;若不存在,说明理由.
