18.1.1 平行四边形的性质 同步练习 2022-2023学年人教版八年级数学下册含答案
文档属性
| 名称 | 18.1.1 平行四边形的性质 同步练习 2022-2023学年人教版八年级数学下册含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 22:51:31 | ||
图片预览


文档简介
18.1.1 平行四边形的性质 同步练习 2022-2023学年人教版八年级数学下册
一、单选题
1.若平行四边形中两内角的度数比为2:3,则其中较小的内角是( )
A. B. C. D.
2.平行四边形具有的特征是( )
A.对角线互相平分 B.对角线相等
C.四个角都是直角 D.四边相等
3.如图,在 ABCD中,∠A=130°,则∠C-∠B的度数为( )
A.90° B.80° C.70° D.60°
4.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
5.如图,在平行四边形中,若,则的度数为( )
A. B. C. D.
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=8,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.3 B.4 C.4 D.3
7.如图,在平行四边形ABCD中,∠BDA=90°,AC=10,BD=6,则AD=( )
A.4 B.5 C.6 D.8
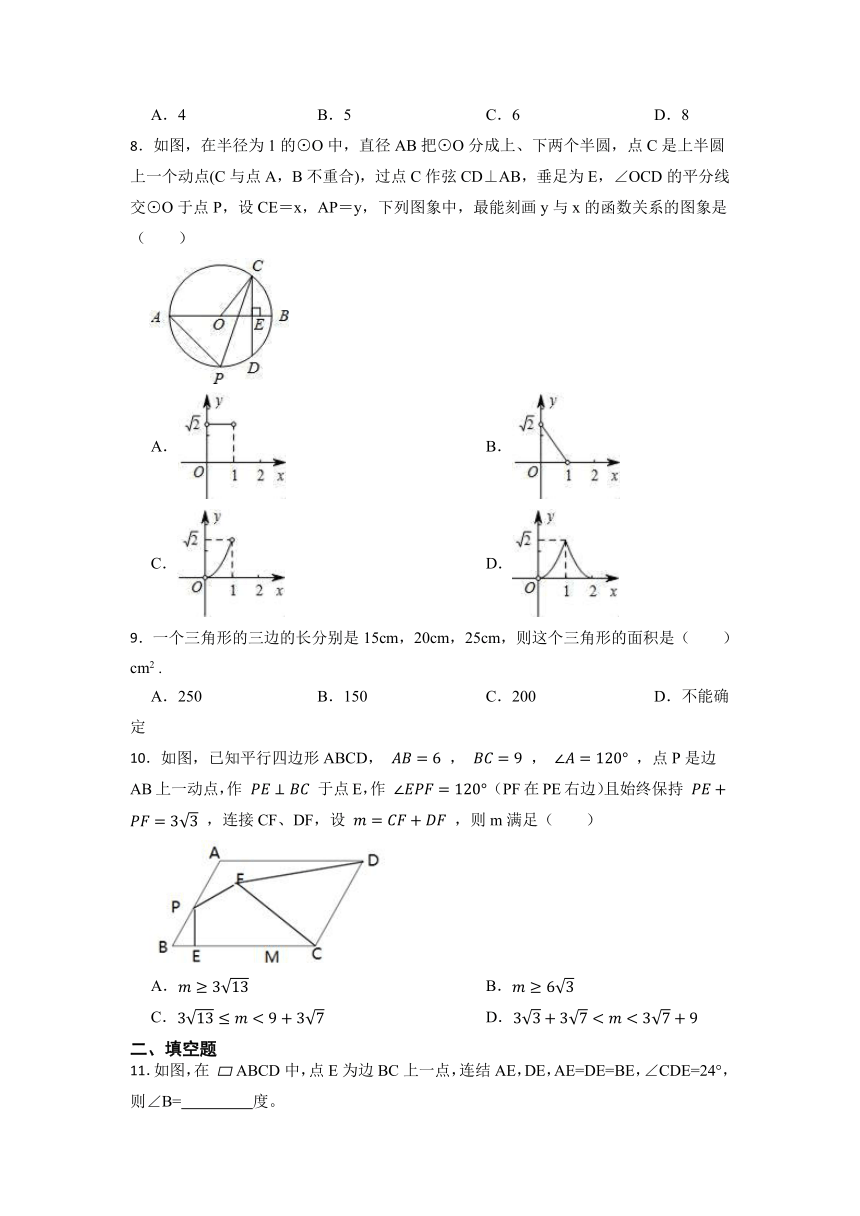
8.如图,在半径为1的⊙O中,直径AB把⊙O分成上、下两个半圆,点C是上半圆上一个动点(C与点A,B不重合),过点C作弦CD⊥AB,垂足为E,∠OCD的平分线交⊙O于点P,设CE=x,AP=y,下列图象中,最能刻画y与x的函数关系的图象是( )
A. B.
C. D.
9.一个三角形的三边的长分别是15cm,20cm,25cm,则这个三角形的面积是( )cm2 .
A.250 B.150 C.200 D.不能确定
10.如图,已知平行四边形ABCD, , , ,点P是边AB上一动点,作 于点E,作 (PF在PE右边)且始终保持 ,连接CF、DF,设 ,则m满足( )
A. B.
C. D.
二、填空题
11.如图,在 ABCD中,点E为边BC上一点,连结AE,DE,AE=DE=BE,∠CDE=24°,则∠B= 度。
12.如图,OP平分 , , , ,则 的面积等于 .
13.如图,平行四边形 , 和 的平分线交于点 ,过点E作EF∥AB交BC于F,连接 并延长交 于 ,若 ,BC=6,则线段 的长为 .
14.如图,过原点的直线与反比例函数 ( )的图象交于 , 两点,点 在第一象限.点 在 轴正半轴上,连结 交反比例函数图象于点 . 为 的平分线,过点 作 的垂线,垂足为 ,连结 .若 是线段 中点, 的面积为4,则 的值为 .
三、解答题
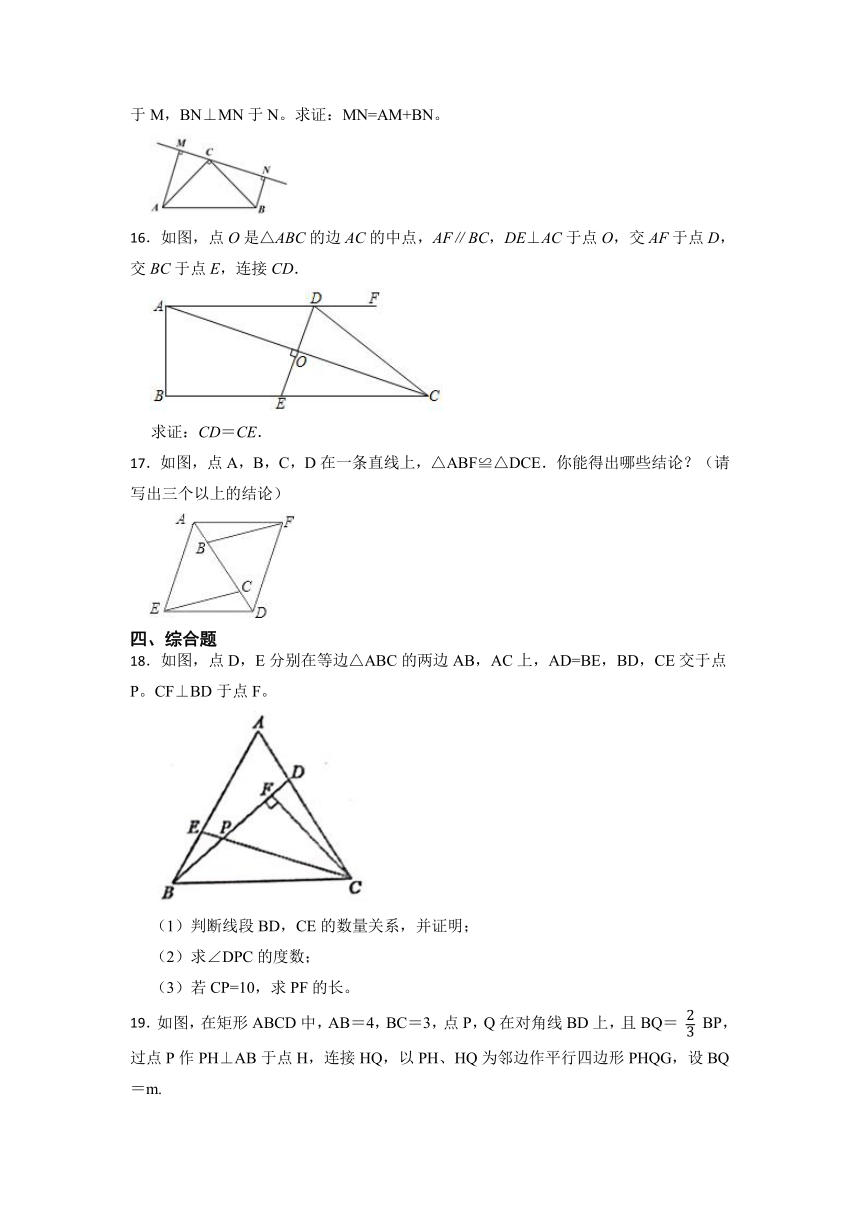
15.如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。求证:MN=AM+BN。
16.如图,点O是△ABC的边AC的中点,AF∥BC,DE⊥AC于点O,交AF于点D,交BC于点E,连接CD.
求证:CD=CE.
17.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
四、综合题
18.如图,点D,E分别在等边△ABC的两边AB,AC上,AD=BE,BD,CE交于点P。CF⊥BD于点F。
(1)判断线段BD,CE的数量关系,并证明;
(2)求∠DPC的度数;
(3)若CP=10,求PF的长。
19.如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ= BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
(1)若m=2时,求此时PH的长.
(2)若点C,G,H在同一直线上时,求此时的m值.
(3)若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】68
12.【答案】
13.【答案】4
14.【答案】
15.【答案】证明:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90 ,
∴∠MAC+∠ACM=90 ,
又∵∠ACB=90 ,
∴∠NCB+∠ACM=90 ,
∴∠MAC=∠NCB.
又∵AC=BC,
∴△ACM≌△CBN,
∴AM=CN,CM=BN,
又∵MN=CN+CM,
∴MN=AM+BN.
16.【答案】证明:∵点O是△ABC的边AC的中点,
∴AO=CO.
∵AD∥BC,
∴∠DAO=∠ECO.
在△AOD和△COE中,
,
∴△AOD≌△COE(ASA),
∴DO=EO.
在△COD和△COE中,
,
∴△COD≌△COE(SAS),
∴CD=CE.
17.【答案】解:∵△ABF≌△DCE
∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;
∴AF∥ED,AC=BD,BF∥CE
18.【答案】(1)证明:∵△ABC是等边三角形,
∴∠A=∠ABC=60°,AB=BC,
又∵AD=BE,
∴△ABD≌△BCE,
∴BD=CE.
(2)解:∵△ABD≌△BCE,
∴∠BCE=∠ABD,
∴∠DPC=∠DBC+∠BCE=∠DBC+∠ABD=∠ABC=60°.
(3)解:∵∠DPC=60°,CF⊥BD,
∴∠PCF=30°,
又∵CP=10,
∴PF=5.
19.【答案】(1)解: 在矩形ABCD中,AB=4,BC=3,
∴BD= = =5,
∵BQ=2, ,
∴BP=3,
∵PH∥AD,
∴△BPH∽△BDA,
∴ ,
∴ ;
(2)解: 如图,设HG与PQ交于点O,
设BQ=2x,则BP=3x,PQ=x,
∴PO=QO= ,
∴BO= x,
∵PH∥BC,
∴△PHO∽△BCO,
∴ ,
∴PH= = ,
∵PH∥AD,
∴△BPH∽△BDA,
∴ ,
∴ ,
∴x= ,
∴BQ= ;
(3)解:连接AC交BD于点O,
∵经过点G的直线将矩形ABCD的面积平分
∴这条直线经过矩形ABCD的对角线的交点,
如图,当直线OG经过PH的中点时,
∵直线OG将平行四边形PHQG的面积分成1:3的两部分
∴PH∥GQ,
∴△PRO∽△GOQ,
∴
∴
解之:;
如图,当直线OG经过HQ的中点N时,
∵直线OG将平行四边形PHQG的面积分成1:3的两部分
∴PG∥HQ,
∴△NOQ∽△POG
∴
∴
解之:;
m的值为或
一、单选题
1.若平行四边形中两内角的度数比为2:3,则其中较小的内角是( )
A. B. C. D.
2.平行四边形具有的特征是( )
A.对角线互相平分 B.对角线相等
C.四个角都是直角 D.四边相等
3.如图,在 ABCD中,∠A=130°,则∠C-∠B的度数为( )
A.90° B.80° C.70° D.60°
4.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
5.如图,在平行四边形中,若,则的度数为( )
A. B. C. D.
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=8,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.3 B.4 C.4 D.3
7.如图,在平行四边形ABCD中,∠BDA=90°,AC=10,BD=6,则AD=( )
A.4 B.5 C.6 D.8
8.如图,在半径为1的⊙O中,直径AB把⊙O分成上、下两个半圆,点C是上半圆上一个动点(C与点A,B不重合),过点C作弦CD⊥AB,垂足为E,∠OCD的平分线交⊙O于点P,设CE=x,AP=y,下列图象中,最能刻画y与x的函数关系的图象是( )
A. B.
C. D.
9.一个三角形的三边的长分别是15cm,20cm,25cm,则这个三角形的面积是( )cm2 .
A.250 B.150 C.200 D.不能确定
10.如图,已知平行四边形ABCD, , , ,点P是边AB上一动点,作 于点E,作 (PF在PE右边)且始终保持 ,连接CF、DF,设 ,则m满足( )
A. B.
C. D.
二、填空题
11.如图,在 ABCD中,点E为边BC上一点,连结AE,DE,AE=DE=BE,∠CDE=24°,则∠B= 度。
12.如图,OP平分 , , , ,则 的面积等于 .
13.如图,平行四边形 , 和 的平分线交于点 ,过点E作EF∥AB交BC于F,连接 并延长交 于 ,若 ,BC=6,则线段 的长为 .
14.如图,过原点的直线与反比例函数 ( )的图象交于 , 两点,点 在第一象限.点 在 轴正半轴上,连结 交反比例函数图象于点 . 为 的平分线,过点 作 的垂线,垂足为 ,连结 .若 是线段 中点, 的面积为4,则 的值为 .
三、解答题
15.如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。求证:MN=AM+BN。
16.如图,点O是△ABC的边AC的中点,AF∥BC,DE⊥AC于点O,交AF于点D,交BC于点E,连接CD.
求证:CD=CE.
17.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
四、综合题
18.如图,点D,E分别在等边△ABC的两边AB,AC上,AD=BE,BD,CE交于点P。CF⊥BD于点F。
(1)判断线段BD,CE的数量关系,并证明;
(2)求∠DPC的度数;
(3)若CP=10,求PF的长。
19.如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ= BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
(1)若m=2时,求此时PH的长.
(2)若点C,G,H在同一直线上时,求此时的m值.
(3)若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】68
12.【答案】
13.【答案】4
14.【答案】
15.【答案】证明:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90 ,
∴∠MAC+∠ACM=90 ,
又∵∠ACB=90 ,
∴∠NCB+∠ACM=90 ,
∴∠MAC=∠NCB.
又∵AC=BC,
∴△ACM≌△CBN,
∴AM=CN,CM=BN,
又∵MN=CN+CM,
∴MN=AM+BN.
16.【答案】证明:∵点O是△ABC的边AC的中点,
∴AO=CO.
∵AD∥BC,
∴∠DAO=∠ECO.
在△AOD和△COE中,
,
∴△AOD≌△COE(ASA),
∴DO=EO.
在△COD和△COE中,
,
∴△COD≌△COE(SAS),
∴CD=CE.
17.【答案】解:∵△ABF≌△DCE
∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;
∴AF∥ED,AC=BD,BF∥CE
18.【答案】(1)证明:∵△ABC是等边三角形,
∴∠A=∠ABC=60°,AB=BC,
又∵AD=BE,
∴△ABD≌△BCE,
∴BD=CE.
(2)解:∵△ABD≌△BCE,
∴∠BCE=∠ABD,
∴∠DPC=∠DBC+∠BCE=∠DBC+∠ABD=∠ABC=60°.
(3)解:∵∠DPC=60°,CF⊥BD,
∴∠PCF=30°,
又∵CP=10,
∴PF=5.
19.【答案】(1)解: 在矩形ABCD中,AB=4,BC=3,
∴BD= = =5,
∵BQ=2, ,
∴BP=3,
∵PH∥AD,
∴△BPH∽△BDA,
∴ ,
∴ ;
(2)解: 如图,设HG与PQ交于点O,
设BQ=2x,则BP=3x,PQ=x,
∴PO=QO= ,
∴BO= x,
∵PH∥BC,
∴△PHO∽△BCO,
∴ ,
∴PH= = ,
∵PH∥AD,
∴△BPH∽△BDA,
∴ ,
∴ ,
∴x= ,
∴BQ= ;
(3)解:连接AC交BD于点O,
∵经过点G的直线将矩形ABCD的面积平分
∴这条直线经过矩形ABCD的对角线的交点,
如图,当直线OG经过PH的中点时,
∵直线OG将平行四边形PHQG的面积分成1:3的两部分
∴PH∥GQ,
∴△PRO∽△GOQ,
∴
∴
解之:;
如图,当直线OG经过HQ的中点N时,
∵直线OG将平行四边形PHQG的面积分成1:3的两部分
∴PG∥HQ,
∴△NOQ∽△POG
∴
∴
解之:;
m的值为或
