北京市海淀外国语2022-2023-2初三年级数学练习PDF版(无答案)
文档属性
| 名称 | 北京市海淀外国语2022-2023-2初三年级数学练习PDF版(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 07:45:45 | ||
图片预览


文档简介
北京市海淀外国语 2022—2023—2 初三年级数学练习
姓名:___________班级:___________
一、单选题(共 16分,每题 2分)
1.下列几何体中,其俯视图与主视图完全相同的是( )
A. B. C. D.
2.据报道,位于丰台区的北京排水集团槐房再生水厂,是亚洲规模最大的一座全地下再
生水厂,日处理污水能力 600000立方米,服务面积 137平方公里.将 600000用科学记数
法表示为( )
A.0.6×105 B.0.6×106 C.6×105 D.6×106
3.一个多边形的每个内角都等于 120°, 则此多边形是( )
A.五边形 B.七边形 C.六边形 D.八边形
4.实数 a、b、c、d在数轴上对应点的位置如图所示,正确的结论有( )
A.a>b B.bc>0 C.|c|>|b| D.b+d>0
5.对于两组数据 A,B 2 2,如果 sA sB ,且 xA xB,则( )
A.这两组数据的波动相同 B.数据 B的波动小一些
C.它们的平均水平不相同 D.数据 A的波动小一些
6.在⊙O中按如下步骤作图:
(1)作⊙O的直径 AD;
(2)以点 D为圆心,DO长为半径画弧,交⊙O于 B,C两点;
(3)连接 DB,DC,AB,AC,BC.
根据以上作图过程及所作图形,下列四个结论中错误的是( )
A.∠ABD=90° B.∠BAD=∠CBD C.AD⊥BC D.AC=2CD
2 2 ab
7.如果 a﹣b=5 a b,那么代数式( ﹣2) 的值是( )
ab a b
1 1
A.﹣ B. C.﹣5 D.5
5 5
8.已知关于 n的函数 s=an2+bn(n为自然数),当 n=9时,s<0;当 n=10时,s>0.则
s的值最小时,n取( ).
A.3 B.4 C.5 D.6
第 1页,共 8页
二、填空题(共 16分,每题 2分)
1
9.使分式 有意义的 x的取值范围是_________.
x 1
10.因式分解 2x2 4x 2 =______.
11.一个不透明的盒子中装有 4个黄球,3个红球和 1个绿球,这些球除了颜色外无其他
差别.从中随机摸出一个小球,恰好是红球的概率是_____.
BF
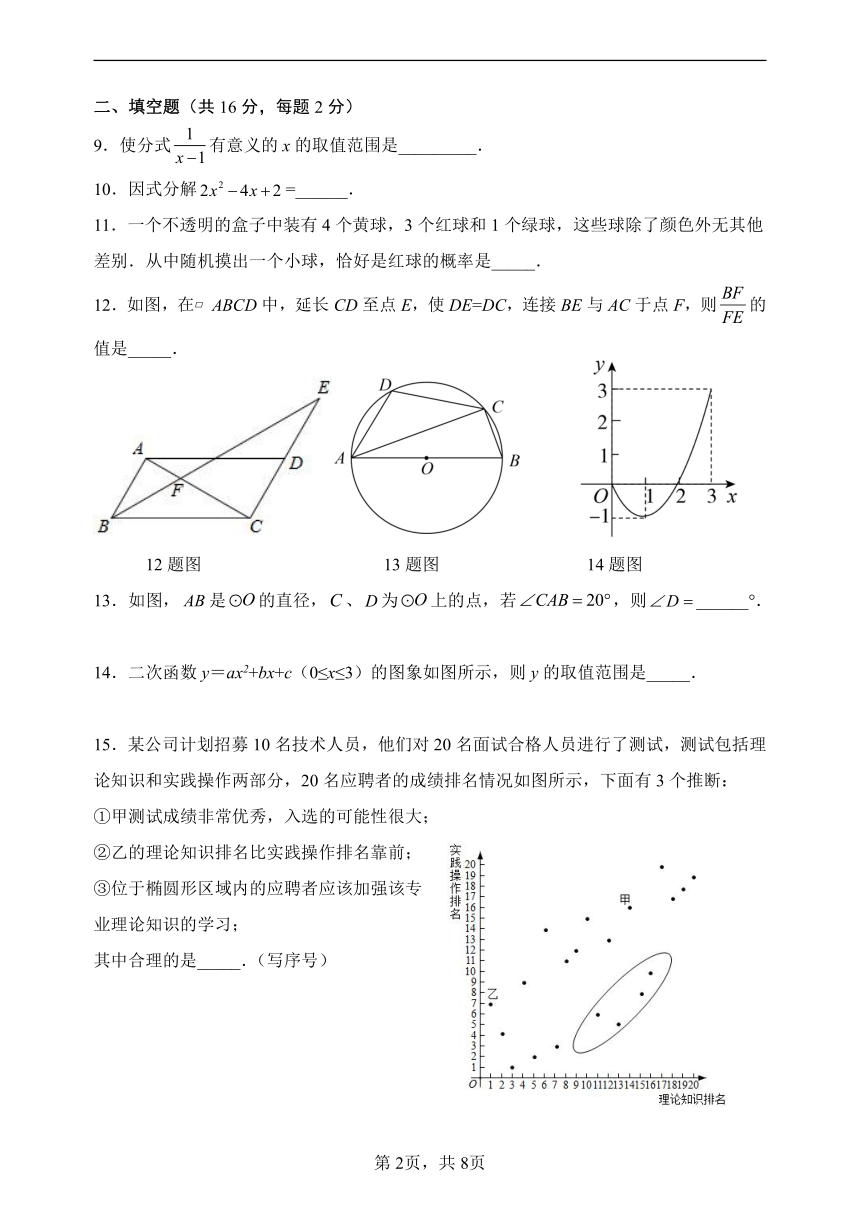
12.如图,在 ABCD中,延长 CD至点 E,使 DE=DC,连接 BE与 AC于点 F,则 的
FE
值是_____.
12题图 13题图 14题图
13.如图, AB是 O的直径,C、D为 O上的点,若 CAB 20 ,则 D ______°.
14.二次函数 y=ax2+bx+c(0≤x≤3)的图象如图所示,则 y的取值范围是_____.
15.某公司计划招募 10名技术人员,他们对 20名面试合格人员进行了测试,测试包括理
论知识和实践操作两部分,20名应聘者的成绩排名情况如图所示,下面有 3个推断:
①甲测试成绩非常优秀,入选的可能性很大;
②乙的理论知识排名比实践操作排名靠前;
③位于椭圆形区域内的应聘者应该加强该专
业理论知识的学习;
其中合理的是_____.(写序号)
第 2页,共 8页
16.标有 1-25号的 25个座位如图摆放.甲、乙、丙、丁四人玩选座位游戏,甲选 2个
座位,乙选 3个座位,丙选 4个座位,丁选 5个座位,游戏规则如下:①每人只能选择同
一横行或同一竖列的座位;②每人使自己所选的座位号数字之和最小;③座位不能重复选
择.如果按“甲、乙、丙、丁”的先后顺序选座位,那
么甲选 1,2号座位,乙选 3,4,5号座位,丙选 7,
8,9,10号座位,丁选 13,14,15,16,17号座位,
此时四人所选的座位号数字之和为 124,如果按“丁、
丙、乙、甲”的先后顺序选座位,那么四人所选的座
位号数字之和为________.
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,第 27-28 题,
每题 7分)
2
17 1 .计算: ( 7)
0 3 2 4sin60 .
2
3x-5>2(x-3) ①
18.解不等式组 并写出该不等式组的所有非负整数解.
x 4
≥x ②
3
19.已知 x2 3x 1 0,求代数式 (x 2)(x 2) x(3x 6)的值.
20.关于 x的一元二次方程 x2﹣2kx+k2+k﹣2=0有两个不相等的实数根.
(1)求 k的取值范围;
(2)若 k为正整数,求 k的值及此时方程的根.
第 3页,共 8页
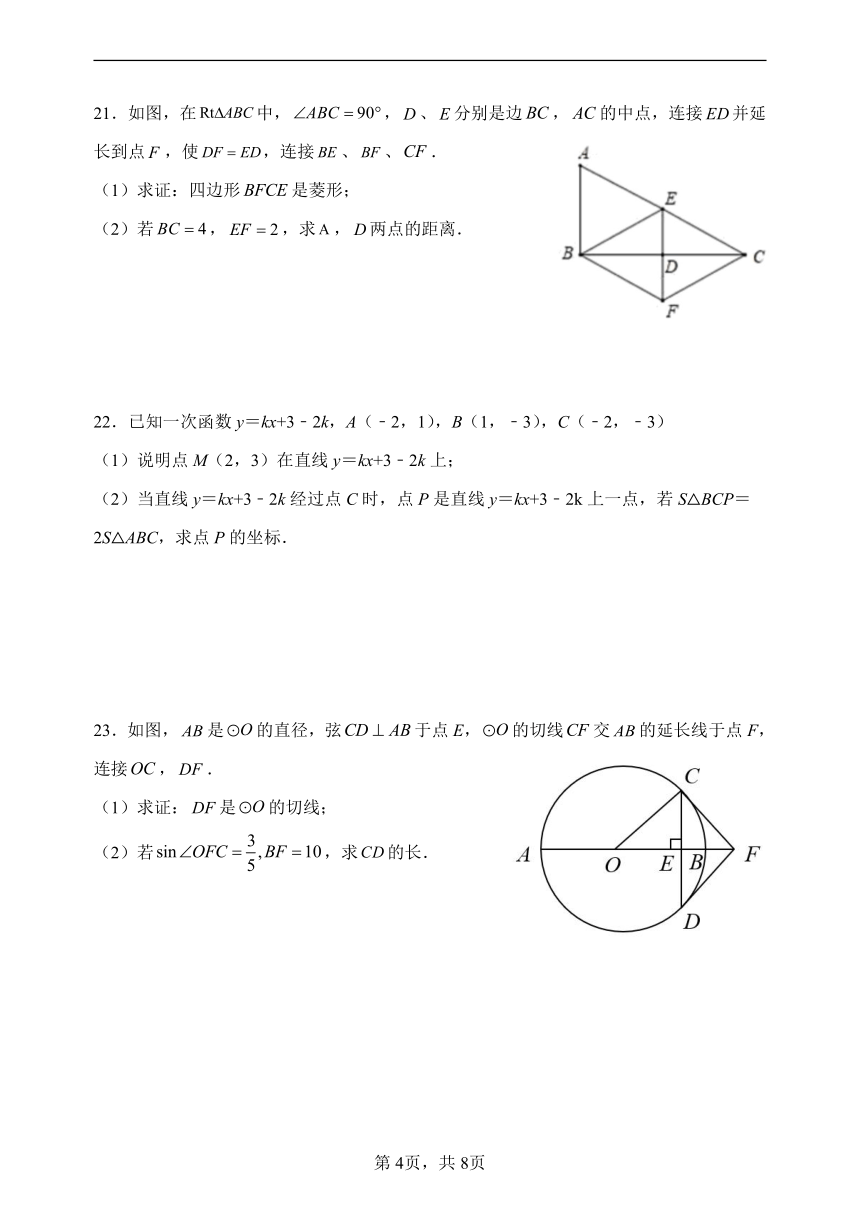
21.如图,在Rt ABC中, ABC 90 ,D、E分别是边 BC, AC的中点,连接 ED并延
长到点 F ,使DF ED,连接 BE、 BF、CF.
(1)求证:四边形BFCE是菱形;
(2)若 BC 4, EF 2,求A,D两点的距离.
22.已知一次函数 y=kx+3﹣2k,A(﹣2,1),B(1,﹣3),C(﹣2,﹣3)
(1)说明点 M(2,3)在直线 y=kx+3﹣2k上;
(2)当直线 y=kx+3﹣2k经过点 C时,点 P是直线 y=kx+3﹣2k上一点,若 S△BCP=
2S△ABC,求点 P的坐标.
23.如图, AB是 O的直径,弦CD AB于点 E, O的切线CF交 AB的延长线于点 F,
连接OC,DF.
(1)求证:DF是 O的切线;
3
(2)若 sin OFC ,BF 10,求CD的长.
5
第 4页,共 8页
24.如图,半圆 O的直径 AB=5cm,点 M在 AB上且 AM=1cm,点 P是半圆 O上的动点,
过点 B作 BQ⊥PM交 PM(或 PM的延长线)于点 Q.设 PM=xcm,BQ=ycm.(当点 P
与点 A或点 B重合时,y的值为 0)小石根据学习函数的经验,对函数 y随自变量 x的变
化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了 x与 y的几组值,如下表:
x/cm 1 1.5 2 2.5 3 3.5 4
y/cm 0 3.7 ______ 3.8 3.3 2.5 ______
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的
图象;
(3)结合画出的函数图象,解决问题:当 BQ与直径 AB所夹的锐角为 60°时,PM的长
度约为______cm.
第 5页,共 8页
25.北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从甲、
乙两个滑雪场的游客中各随机抽取了 50人,获得了这些游客当天消费额(单位:元)的
数据,并对数据进行整理、描述和分析.下面给出部分信息:
a.甲滑雪场游客消费额的数据的频数分布直方图如下(数据分成 6组:0≤x<200,
200≤x<400,400≤x<600,600≤x<800,800≤x<1000,1000≤x<1200):
b.甲滑雪场游客消费额的数据在 400≤x<600这一组的是:
410 430 430 440 440 440 450 450 520 540
c.甲、乙两个滑雪场游客消费额的数据的平均数、中位数如下:
平均数 中位数
甲滑雪场 420 m
乙滑雪场 390 n
根据以上信息,回答下列问题:
(1)写出表中 m=_____
(2)一名被调查的游客当天的消费额为 380元,在他所在的滑雪场,他的消费额超过了
一半以上的被调查的游客,那么他是哪个滑雪场的游客?请说明理由;
(3)若乙滑雪场当天的游客人数为 500人,估计乙滑雪场这个月(按 30天计算)的游客
消费总额.
第 6页,共 8页
26.在直角坐标系 xOy中,点 A(t,2)(t≠0)在二次函数 y ax 2 bx 2(a 0)的图象上.
(1)当 t 4时,求抛物线对称轴的表达式;
(2)若点 B(5 t, 0)也在这个二次函数的图象上.
①当这个函数的最小值为 0时,求 t的值;
②若在 0 x 1时,y随 x的增大而增大,求 t的取值范围.
27.△ABC中,AB=BC,∠ABC=90°,将线段 AB绕点 A逆时针旋转α(0°<α<90°)得
到线段 AD.作射线 BD,点 C关于射线 BD的对称点为点 E.连接 AE,CE.
(1)依题意补全图形;
(2)若α=20°,直接写出∠AEC的度数;
(3)写出一个α的值,使 AE= 2时,线段 CE的长为 3﹣1,并证明.
第 7页,共 8页
28.对于平面直角坐标系 xOy中的图形M ,N,给出如下定义:P为图形M 上任意一点,
Q为图形 N上任意一点,如果 P,Q两点间的距离有最小值,那么称这个最小值为图形M ,
N间的“闭距离”,记作d (M , N).
已知点A( 2,6), B( 2, 2),C(6, 2).
(1)求d (点O, ABC);
(2)记函数 y kx( 1 x 1,k 0)的图象为图形G,若d (G, ABC) 1,直接
写出 k的取值范围;
(3) T 的圆心为T(t,0),半径为 1.若d ( T , ABC) 1,直接写出 t的取值范
围.
第 8页,共 8页
姓名:___________班级:___________
一、单选题(共 16分,每题 2分)
1.下列几何体中,其俯视图与主视图完全相同的是( )
A. B. C. D.
2.据报道,位于丰台区的北京排水集团槐房再生水厂,是亚洲规模最大的一座全地下再
生水厂,日处理污水能力 600000立方米,服务面积 137平方公里.将 600000用科学记数
法表示为( )
A.0.6×105 B.0.6×106 C.6×105 D.6×106
3.一个多边形的每个内角都等于 120°, 则此多边形是( )
A.五边形 B.七边形 C.六边形 D.八边形
4.实数 a、b、c、d在数轴上对应点的位置如图所示,正确的结论有( )
A.a>b B.bc>0 C.|c|>|b| D.b+d>0
5.对于两组数据 A,B 2 2,如果 sA sB ,且 xA xB,则( )
A.这两组数据的波动相同 B.数据 B的波动小一些
C.它们的平均水平不相同 D.数据 A的波动小一些
6.在⊙O中按如下步骤作图:
(1)作⊙O的直径 AD;
(2)以点 D为圆心,DO长为半径画弧,交⊙O于 B,C两点;
(3)连接 DB,DC,AB,AC,BC.
根据以上作图过程及所作图形,下列四个结论中错误的是( )
A.∠ABD=90° B.∠BAD=∠CBD C.AD⊥BC D.AC=2CD
2 2 ab
7.如果 a﹣b=5 a b,那么代数式( ﹣2) 的值是( )
ab a b
1 1
A.﹣ B. C.﹣5 D.5
5 5
8.已知关于 n的函数 s=an2+bn(n为自然数),当 n=9时,s<0;当 n=10时,s>0.则
s的值最小时,n取( ).
A.3 B.4 C.5 D.6
第 1页,共 8页
二、填空题(共 16分,每题 2分)
1
9.使分式 有意义的 x的取值范围是_________.
x 1
10.因式分解 2x2 4x 2 =______.
11.一个不透明的盒子中装有 4个黄球,3个红球和 1个绿球,这些球除了颜色外无其他
差别.从中随机摸出一个小球,恰好是红球的概率是_____.
BF
12.如图,在 ABCD中,延长 CD至点 E,使 DE=DC,连接 BE与 AC于点 F,则 的
FE
值是_____.
12题图 13题图 14题图
13.如图, AB是 O的直径,C、D为 O上的点,若 CAB 20 ,则 D ______°.
14.二次函数 y=ax2+bx+c(0≤x≤3)的图象如图所示,则 y的取值范围是_____.
15.某公司计划招募 10名技术人员,他们对 20名面试合格人员进行了测试,测试包括理
论知识和实践操作两部分,20名应聘者的成绩排名情况如图所示,下面有 3个推断:
①甲测试成绩非常优秀,入选的可能性很大;
②乙的理论知识排名比实践操作排名靠前;
③位于椭圆形区域内的应聘者应该加强该专
业理论知识的学习;
其中合理的是_____.(写序号)
第 2页,共 8页
16.标有 1-25号的 25个座位如图摆放.甲、乙、丙、丁四人玩选座位游戏,甲选 2个
座位,乙选 3个座位,丙选 4个座位,丁选 5个座位,游戏规则如下:①每人只能选择同
一横行或同一竖列的座位;②每人使自己所选的座位号数字之和最小;③座位不能重复选
择.如果按“甲、乙、丙、丁”的先后顺序选座位,那
么甲选 1,2号座位,乙选 3,4,5号座位,丙选 7,
8,9,10号座位,丁选 13,14,15,16,17号座位,
此时四人所选的座位号数字之和为 124,如果按“丁、
丙、乙、甲”的先后顺序选座位,那么四人所选的座
位号数字之和为________.
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,第 27-28 题,
每题 7分)
2
17 1 .计算: ( 7)
0 3 2 4sin60 .
2
3x-5>2(x-3) ①
18.解不等式组 并写出该不等式组的所有非负整数解.
x 4
≥x ②
3
19.已知 x2 3x 1 0,求代数式 (x 2)(x 2) x(3x 6)的值.
20.关于 x的一元二次方程 x2﹣2kx+k2+k﹣2=0有两个不相等的实数根.
(1)求 k的取值范围;
(2)若 k为正整数,求 k的值及此时方程的根.
第 3页,共 8页
21.如图,在Rt ABC中, ABC 90 ,D、E分别是边 BC, AC的中点,连接 ED并延
长到点 F ,使DF ED,连接 BE、 BF、CF.
(1)求证:四边形BFCE是菱形;
(2)若 BC 4, EF 2,求A,D两点的距离.
22.已知一次函数 y=kx+3﹣2k,A(﹣2,1),B(1,﹣3),C(﹣2,﹣3)
(1)说明点 M(2,3)在直线 y=kx+3﹣2k上;
(2)当直线 y=kx+3﹣2k经过点 C时,点 P是直线 y=kx+3﹣2k上一点,若 S△BCP=
2S△ABC,求点 P的坐标.
23.如图, AB是 O的直径,弦CD AB于点 E, O的切线CF交 AB的延长线于点 F,
连接OC,DF.
(1)求证:DF是 O的切线;
3
(2)若 sin OFC ,BF 10,求CD的长.
5
第 4页,共 8页
24.如图,半圆 O的直径 AB=5cm,点 M在 AB上且 AM=1cm,点 P是半圆 O上的动点,
过点 B作 BQ⊥PM交 PM(或 PM的延长线)于点 Q.设 PM=xcm,BQ=ycm.(当点 P
与点 A或点 B重合时,y的值为 0)小石根据学习函数的经验,对函数 y随自变量 x的变
化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了 x与 y的几组值,如下表:
x/cm 1 1.5 2 2.5 3 3.5 4
y/cm 0 3.7 ______ 3.8 3.3 2.5 ______
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的
图象;
(3)结合画出的函数图象,解决问题:当 BQ与直径 AB所夹的锐角为 60°时,PM的长
度约为______cm.
第 5页,共 8页
25.北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从甲、
乙两个滑雪场的游客中各随机抽取了 50人,获得了这些游客当天消费额(单位:元)的
数据,并对数据进行整理、描述和分析.下面给出部分信息:
a.甲滑雪场游客消费额的数据的频数分布直方图如下(数据分成 6组:0≤x<200,
200≤x<400,400≤x<600,600≤x<800,800≤x<1000,1000≤x<1200):
b.甲滑雪场游客消费额的数据在 400≤x<600这一组的是:
410 430 430 440 440 440 450 450 520 540
c.甲、乙两个滑雪场游客消费额的数据的平均数、中位数如下:
平均数 中位数
甲滑雪场 420 m
乙滑雪场 390 n
根据以上信息,回答下列问题:
(1)写出表中 m=_____
(2)一名被调查的游客当天的消费额为 380元,在他所在的滑雪场,他的消费额超过了
一半以上的被调查的游客,那么他是哪个滑雪场的游客?请说明理由;
(3)若乙滑雪场当天的游客人数为 500人,估计乙滑雪场这个月(按 30天计算)的游客
消费总额.
第 6页,共 8页
26.在直角坐标系 xOy中,点 A(t,2)(t≠0)在二次函数 y ax 2 bx 2(a 0)的图象上.
(1)当 t 4时,求抛物线对称轴的表达式;
(2)若点 B(5 t, 0)也在这个二次函数的图象上.
①当这个函数的最小值为 0时,求 t的值;
②若在 0 x 1时,y随 x的增大而增大,求 t的取值范围.
27.△ABC中,AB=BC,∠ABC=90°,将线段 AB绕点 A逆时针旋转α(0°<α<90°)得
到线段 AD.作射线 BD,点 C关于射线 BD的对称点为点 E.连接 AE,CE.
(1)依题意补全图形;
(2)若α=20°,直接写出∠AEC的度数;
(3)写出一个α的值,使 AE= 2时,线段 CE的长为 3﹣1,并证明.
第 7页,共 8页
28.对于平面直角坐标系 xOy中的图形M ,N,给出如下定义:P为图形M 上任意一点,
Q为图形 N上任意一点,如果 P,Q两点间的距离有最小值,那么称这个最小值为图形M ,
N间的“闭距离”,记作d (M , N).
已知点A( 2,6), B( 2, 2),C(6, 2).
(1)求d (点O, ABC);
(2)记函数 y kx( 1 x 1,k 0)的图象为图形G,若d (G, ABC) 1,直接
写出 k的取值范围;
(3) T 的圆心为T(t,0),半径为 1.若d ( T , ABC) 1,直接写出 t的取值范
围.
第 8页,共 8页
同课章节目录
